动态规划简明教程 - 1
📖 概述
在计算机科学中,动态规划(Dynamic Programming,简称 DP)是一种解决复杂问题的方法,通过将问题分解成更小的子问题,并保存子问题的解来避免重复计算。
三个关键特征
下面以 Fibonacci (斐波那契数列) 问题为例,说明动态规划的三个关键特征。
1. 重叠子问题
指在解决问题的过程中需要多次解决相同的子问题,虽然该性质并不是动态规划的使用必要条件,但如果没有该性质,动态规划相比其他算法就不具备明显优势。
计算 Fibonacci 数列时,存在大量的重叠子问题,即同一个 Fibonacci 数列中的某些数字可能会在不同的计算路径中重复出现。
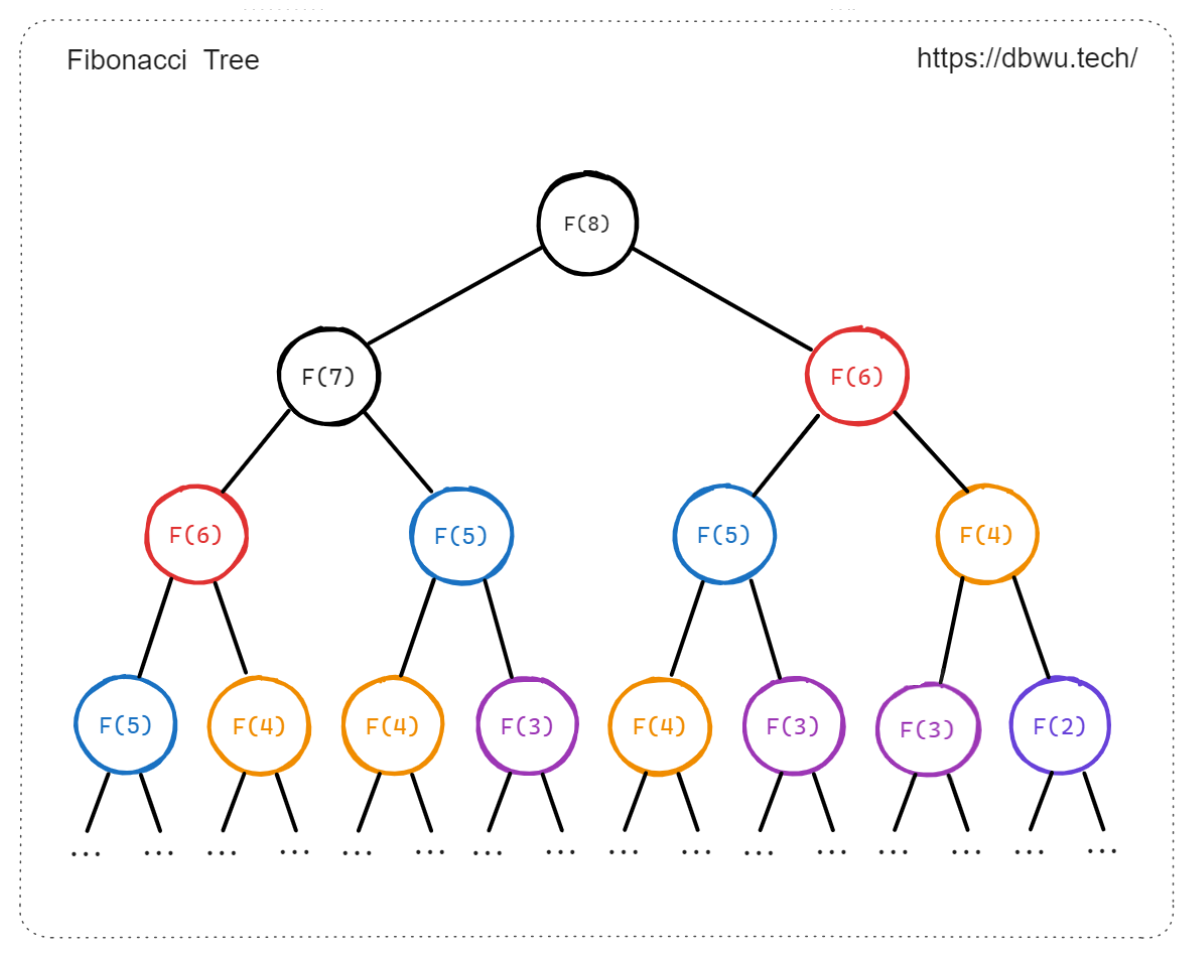
例如计算 F(5) 时需要计算 F(4) 和 F(3),而计算 F(4) 时也需要计算 F(3),这样就会导致 F(3) 这个子问题被重复计算了。
2. 最优子结构
指问题的最优解可以通过子问题的最优解来构造。
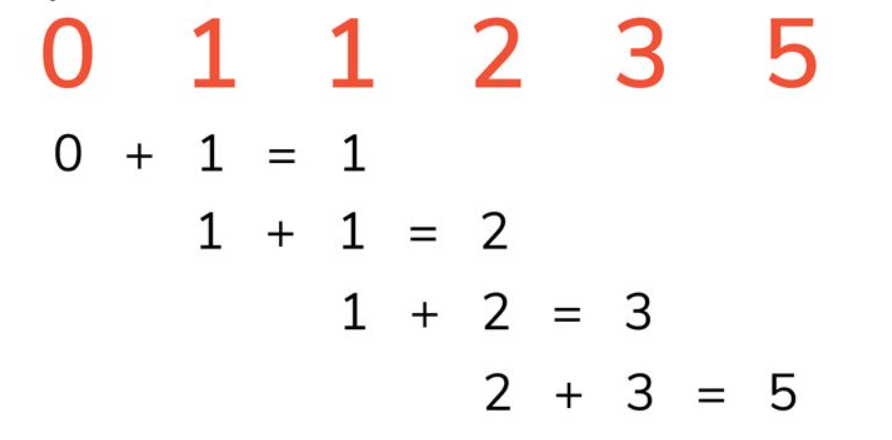
假设需要计算 第 N 个 Fibonacci 数字,可以先计算出该问题的子问题: 也就是 第 N - 1 和 第 N - 2 个 Fibonacci 数字,而第 第 N - 1 个 Fibonacci 数字又可以通过 第 N - 2 和 第 N - 3 个 Fibonacci 数字计算得出,可以自顶向下不停递推,直到达到最基本的情况 (N = 0 和 N = 1 时)。因此,Fibonacci 问题具有最优子结构,每个 Fibonacci 数字可以通过其子问题最优解来构造。
3. 无后效性
对于一个问题当前状态的解,只与问题之前的状态有关,不会受到问题后续 (下一步) 状态的影响。
对于一个问题后续 (下一步) 的解,只与问题当前的状态有关,不会受到问题之前状态的影响。
假设需要计算 第 3 个 Fibonacci 数字,只需要知道 第 2 个 和 第 1 个 Fibonacci 数字,不需要知道 第 3 个 之后的其他 Fibonacci 数字。
状态转移方程
设计正确的状态转移方程是解决动态规划问题的前提。
状态转移顺序的核心是要保证在计算当前问题的解时,所有它依赖的更小子问题的解都已经被正确地计算出来。
动态规划的子问题分解属于自顶向下的思想,因此在解题时可以按照 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 的顺序来实现代码,这样循序渐进地优化更符合我们的思考过程,也可以降低我们从一开始直接推导状态转移方程的心理压力。
将问题的解表示为一个二维或多维数组,数组中的每个元素对应问题的一个状态,通过填表的方式逐步计算并存储问题的解。首先确定问题的状态表示方式并创建一个状态转移表,然后根据问题的状态转移方程,逐个填写表格中的元素值,直到得到原问题的解。
算法步骤
- 定义问题状态:将原问题分解成更小的子问题,并定义问题的状态,通常需要考虑状态的维度和含义
- 状态转移方程:根据问题的最优子结构性质,确定问题状态之间的转移关系,也就是如何从一个状态转移到另一个状态
- 初始化:初始化问题的边界状态,建立状态转移表 (例如一个二维数组),是将问题的边界情况单独处理 (和递归过程中的递归结束条件、边界处理一样)
- 计算子问题:按照状态转移方程计算子问题的状态,并保存中间结果
- 计算原问题:通过逐步子问题的解,最终计算出原问题的解
对应的伪代码如下:
func dp(n, m int) int {
// 定义状态
// 这里使用二维数组来表示子问题的解
state := make([][]int, n+1)
for i := range state {
state[i] = make([]int, m+1)
}
// 初始化
for i := 0; i <= n; i++ {
...
}
for j := 0; j <= m; j++ {
...
}
for i := 1; i <= n; i++ {
for j := 1; j <= m; j++ {
// 4. 计算子问题并保存中间结果
// 这里要用到状态转移方程
...
}
}
return state[n][m]
}
💡 实现过程优化
为了帮助读者理解动态规划的优化过程,这里以 Fibonacci (斐波那契数列) 问题为例,按照 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 的顺序来实现代码,展现三种不同的实现方式之间的性能差异、以及代码实现如何从自顶向下转换为自底向上。
Fibonacci 状态转移方程:
$$ \begin{align*} F(0) &= 0 \\ F(1) &= 1 \\ F(n) &= F(n-1) + F(n-2) \end{align*} $$
1. 暴力搜索
暴力搜索就是将状态转移方程直观地转换为 “自顶向下” 的递归代码。
func fib(n int) int {
if n <= 1 {
return n
}
return fib(n-1) + fib(n-2)
}
暴力搜索实现简单背后的代价是算法时间复杂度很高,对于数字 N, 递归执行的深度为 N, 时间复杂度为 O(2^N),数字 N 越大,指数变化呈爆炸增长。

时间复杂度呈指数增长是因为 “重叠子问题” 导致的,例如图中所示的,计算 Fib(8) 时会递归计算 Fib(7) 和 Fib(6), 然后计算 Fib(7) 时会递归计算 Fib(6) 和 Fib(5), 其中 Fib(6) 被重复计算了,以此类推,递归层数越深,重叠子问题导致的重复计算就会越多。
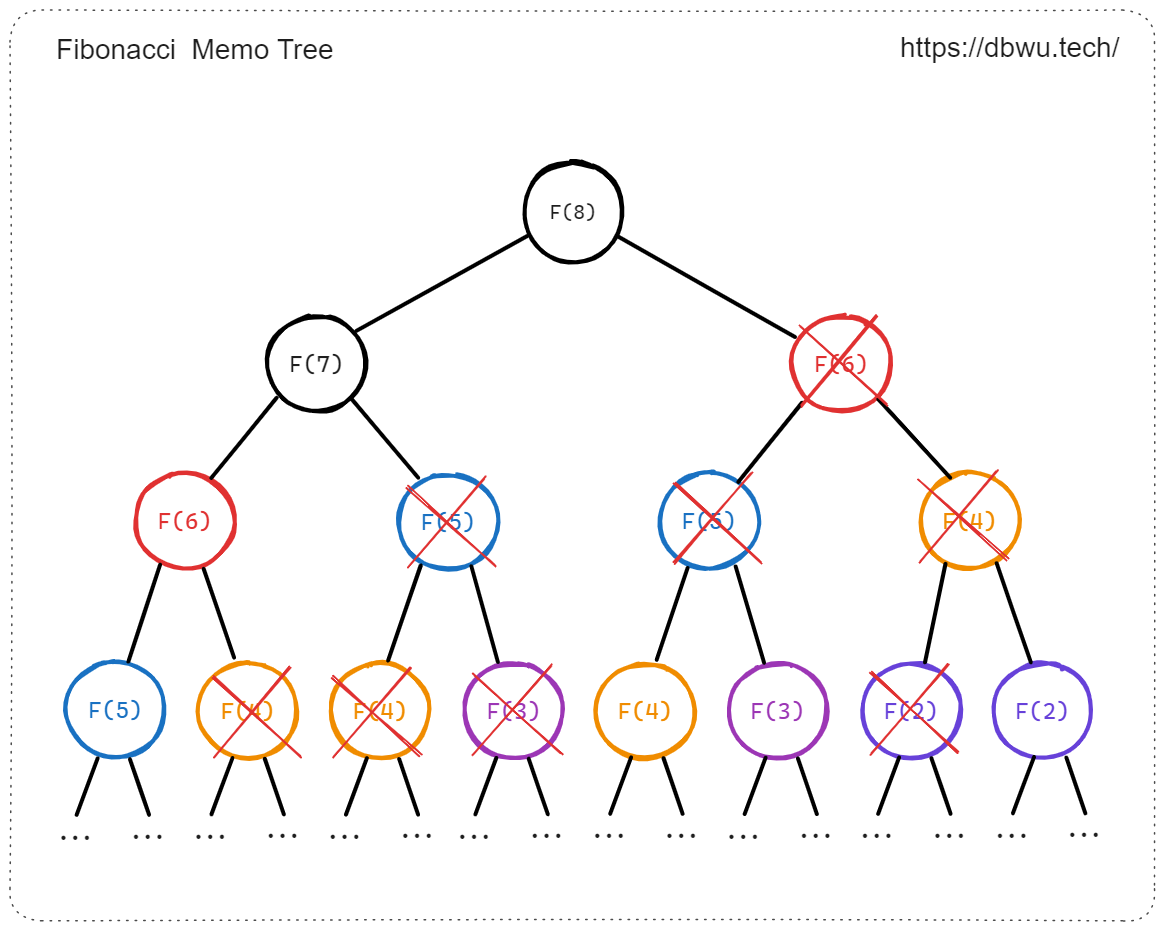
2. 记忆化搜索
记忆化搜索和暴力搜索一样,也属于 “自顶向下” 的递归实现,但是会额外增加一个备忘录 (Memo, 一般使用 HashMap 作为数据结构实现) 来保存已经计算过的问题解,避免重复计算。
通过递归调用解决子问题时,首先检查备忘录中是否已经存在该子问题的解,如果存在,直接返回即可,否则就计算子问题的解,并在计算完成后将解记录到备忘录中。
func fib(n int) int {
memo := make([]int, n+1)
for i := range memo {
memo[i] = -1
}
return fibMem(n, memo)
}
func fibMem(n int, memo []int) int {
if n <= 1 {
return n
}
if memo[n] != -1 {
return memo[n]
}
memo[n] = fibMem(n-1, memo) + fibMem(n-2, memo)
return memo[n]
}
从暴力搜索优化到记忆化搜索之后,程序性能会发生质的变化,因为暴力搜索中所有的重复计算全部优化成为一次计算。
3. 动态规划
动态规划是一种 “自底向上” 的方法,尝试从最小的问题开始,逐步构建问题的解,通过循环迭代的方式,首先解决最小的问题,然后将解保存起来,然后利用已经解决的子问题逐步解决规模更大的子问题,直到解决原问题。
func fib(n int) int {
if n <= 1 {
return n
}
dp := make([]int, n+1)
dp[0], dp[1] = 0, 1
for i := 2; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
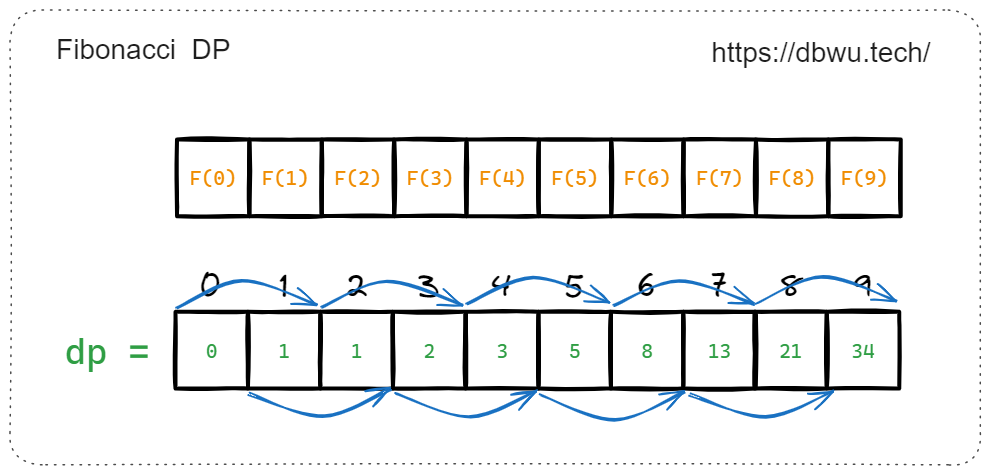
和记忆化搜索一样,动态规划也通过存储中间结果来避免重复计算,但是动态规划采用循环迭代来实现,相比记忆化搜索的递归实现,省去了递归过程中的函数调用和额外的堆栈分配与释放带来的开销,所以性能和内存占用优于记忆化搜索。
状态压缩优化
在 “状态转移表” 的基础上进行空间优化,通常是将多维数组压缩为一维数组甚至少数几个变量,节省内存空间。通过状态之间的转移关系和依赖关系,只保留状态变化过程中的必要变量,并利用这些变量来表示问题的解空间并逐步求解,这种空间优化技巧一般被称为 “滚动变量” 或 “滚动数组”。
func fib(n int) int {
if n <= 1 {
return n
}
prev, cur := 0, 1
for i := 2; i <= n; i++ {
prev, cur = cur, prev+cur
}
return cur
}
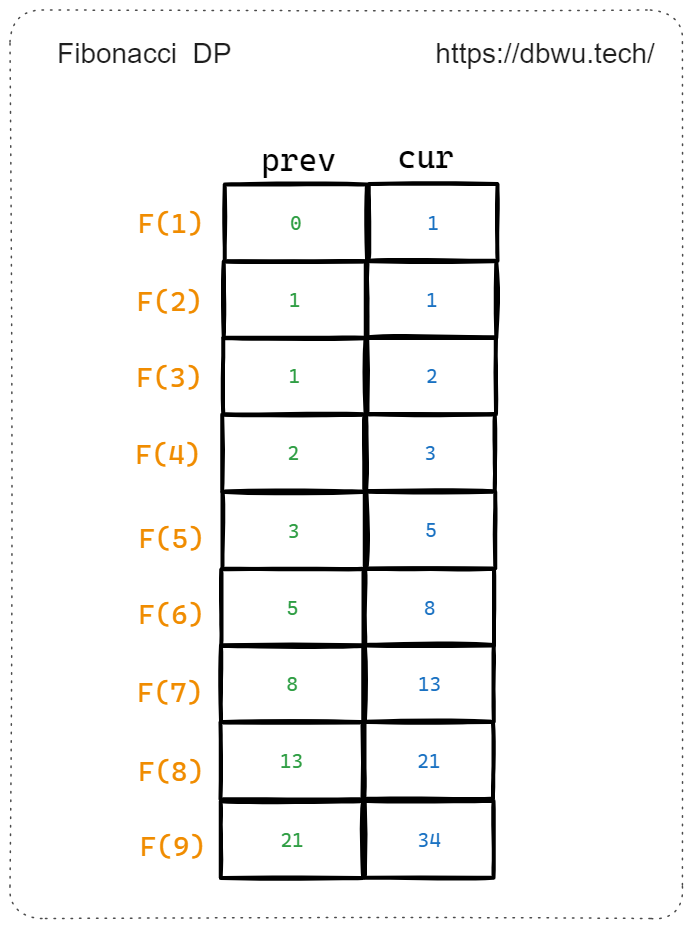
基准测试
为了更加直观地体现出动态规划的算法优势,下面对 Fibonacci 数列的三种实现 暴力搜索、记忆化搜索、动态规划 做一个简陋的的基准测试。
为了节省基准测试运行时间,将 Fibonacci 数固定为 20。
// 暴力搜索基准测试
func BenchmarkFibBruteForce(b *testing.B) {
for i := 0; i < b.N; i++ {
_ = fibBruteForce(20)
}
}
// 记忆化搜索基准测试
func BenchmarkFibMem(b *testing.B) {
for i := 0; i < b.N; i++ {
_ = fibMem(20)
}
}
// 动态规划基准测试
func BenchmarkFibDp(b *testing.B) {
for i := 0; i < b.N; i++ {
_ = fibDp(20)
}
}
// 动态规划状态压缩优化基准测试
func BenchmarkFibDpOpt(b *testing.B) {
for i := 0; i < b.N; i++ {
_ = fibDpOpt(20)
}
}
运行上面的基准测试:
$ go test -bench=. -benchmem
基准测试输出如下:
goos: linux
goarch: amd64
BenchmarkFibBruteForce-8 39777 29989 ns/op 0 B/op 0 allocs/op
BenchmarkFibMem-8 7660668 147.7 ns/op 176 B/op 1 allocs/op
BenchmarkFibDp-8 15572442 69.73 ns/op 176 B/op 1 allocs/op
BenchmarkFibDpOpt-8 180644320 7.205 ns/op 0 B/op 0 allocs/op
PASS
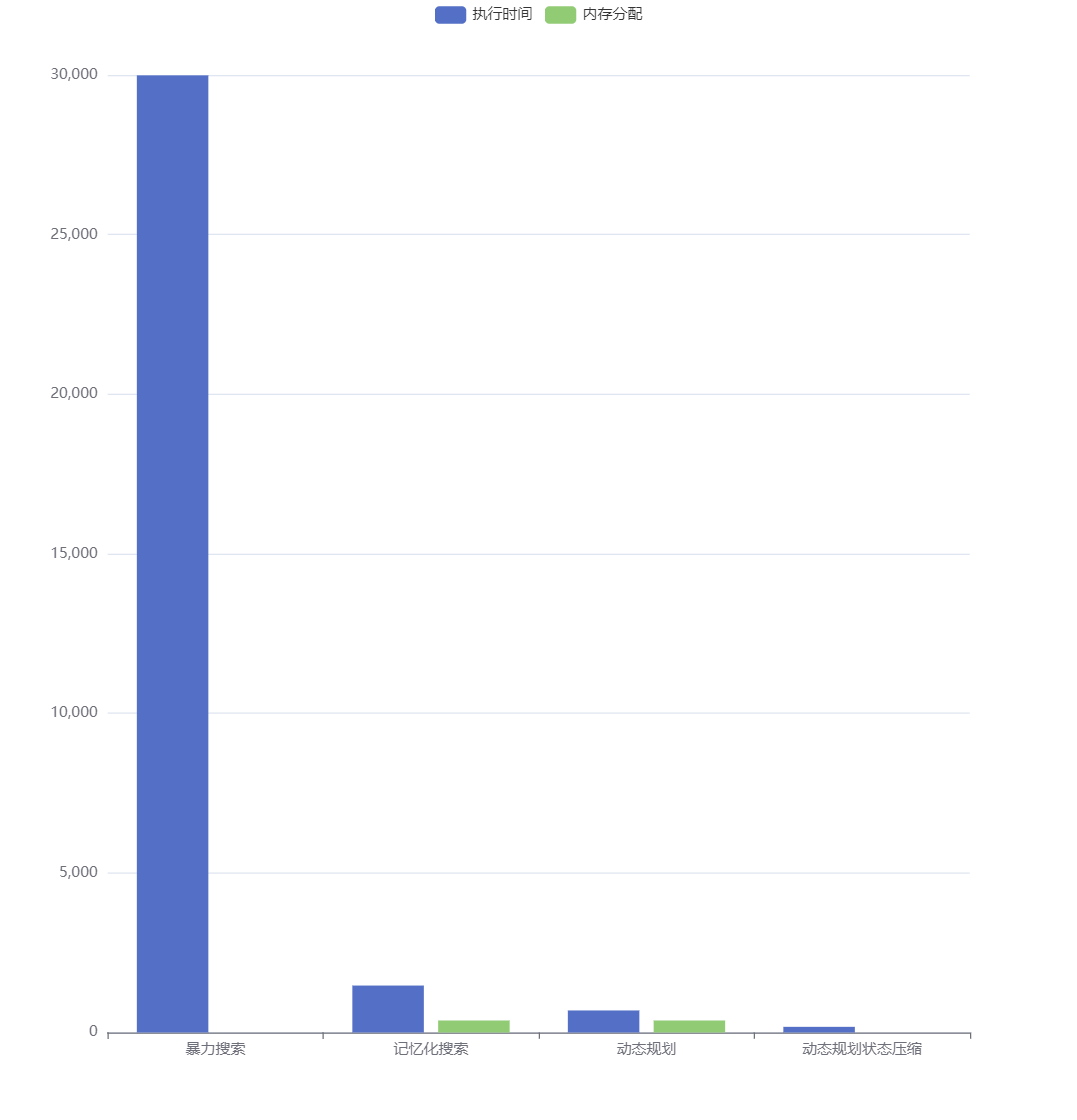
根据基准测试的输出结果,我们可以看到:
- 从暴力搜索优化到记忆化搜索,性能提升了 200 倍,同时内存分配增加
- 从记忆化搜索优化到动态规划,性能提升了 2 倍,内存使用不变
- 动态规划使用状态压缩优化之后,性能再次提升了将近 10 倍,同时内存分配降为 0
小结
本文以 Fibonacci 问题为例,描述了动态规划的基本概念和特征,并且对比了动态规划自顶向下 (暴力搜索、记忆化搜索) 和自底向上的两种实现方式和性能差异,接下来,笔者会从 LeetCode 中选择一些经典的动态规划题目进行练习和讲解,帮助读者巩固和提高动态规划算法技巧。
