动态规划简明教程 - 2
❓ 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
# 示例来自: https://leetcode.cn/
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
💡 解题过程
动态规划的子问题分解属于自顶向下的思想,因此在解题时可以按照 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 的顺序来实现代码,这样循序渐进地优化更符合我们的思考过程,也可以降低我们从一开始直接推导状态转移方程的心理压力。
接下来,我们先尝试着给出一个可行的题解,然后在这个基础上慢慢迭代优化。
解题方法函数原型:
func rob(nums []int) int {}
单元测试
为了节省篇幅,这里给出针对本题的单元测试代码,不管 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 哪种实现方式,都可以直接运行该单元测试。
func Test_rob(t *testing.T) {
type args struct {
nums []int
}
tests := []struct {
name string
args args
want int
}{
{
"test-1",
args{[]int{0}},
0,
},
{
"test-2",
args{[]int{1}},
1,
},
{
"test-3",
args{[]int{1, 2}},
2,
},
{
"test-4",
args{[]int{1, 2, 3}},
4,
},
{
"test-5",
args{[]int{1, 2, 3, 4}},
6,
},
{
"test-6",
args{[]int{2, 7, 9, 3, 1}},
12,
},
{
"test-7",
args{[]int{2, 1}},
2,
},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := rob(tt.args.nums); got != tt.want {
t.Errorf("rob() = %v, want %v", got, tt.want)
}
})
}
}
💪 暴力搜索
解题思路:
我们可以将参数列表想象成一排房屋,任务是计算从第一个房屋走到最后一个房屋,可以偷取到的最大金额。
对于每一个房屋,我们有两种选择:
- 偷取当前房屋,然后再去偷取下下一个房屋 (因为偷取下一个房屋会引发报警),这样可以得到
nums[cur] + nums[cur+2]的金额 - 不偷取当前房屋,直接去偷取下一个房屋,这样可以得到
nums[cur+1]的金额 - 两者之间的最大值就是单次可以偷取到的最大金额
举例来说,我们从第 1 个房屋开始,分别偷取第 1, 3, 5 个房屋,可以偷取到的金额是 2 + 9 + 1 = 12,也可以从第 2 个房屋开始,分别偷取第 2, 4 个房屋,可以偷取到的金额是 7 + 3 = 10。
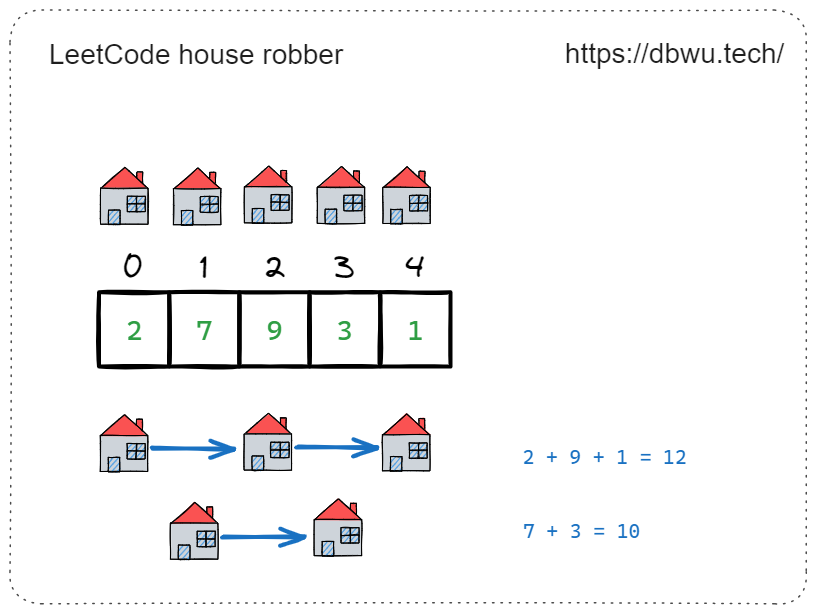
实现代码
根据上面的解题思路,可以写出如下的递归代码:
// 题解代码
// 暴力搜索 (超时)
// 超时原因: 重复检测
func robBruteForce(nums []int) int {
return robFrom(nums, 0)
}
func robFrom(nums []int, begin int) int {
if begin >= len(nums) {
return 0
}
// 偷取当前房屋
// 偷取完当前房屋后,跳过下一个房屋,去偷下下一个房屋
steal := nums[begin] + robFrom(nums, begin+2)
// 不偷取当前房屋
// 去偷下一个房屋
skip := robFrom(nums, begin+1)
// 返回两种偷取方案种的最大值
return max(steal, skip)
}
提交超时
运行单元测试:
$ go test -v -count=1 .
输出结果如下:
=== RUN Test_rob
=== RUN Test_rob/test-1
=== RUN Test_rob/test-2
=== RUN Test_rob/test-3
=== RUN Test_rob/test-4
=== RUN Test_rob/test-5
=== RUN Test_rob/test-6
=== RUN Test_rob/test-7
--- PASS: Test_rob (0.00s)
--- PASS: Test_rob/test-1 (0.00s)
--- PASS: Test_rob/test-2 (0.00s)
--- PASS: Test_rob/test-3 (0.00s)
--- PASS: Test_rob/test-4 (0.00s)
--- PASS: Test_rob/test-5 (0.00s)
--- PASS: Test_rob/test-6 (0.00s)
--- PASS: Test_rob/test-7 (0.00s)
PASS
ok leetcode/0198.House-Robber 0.002s
单元测试全部通过,表面上来看,我们的暴力搜索实现没有问题,现在去官方提交看看运行结果。
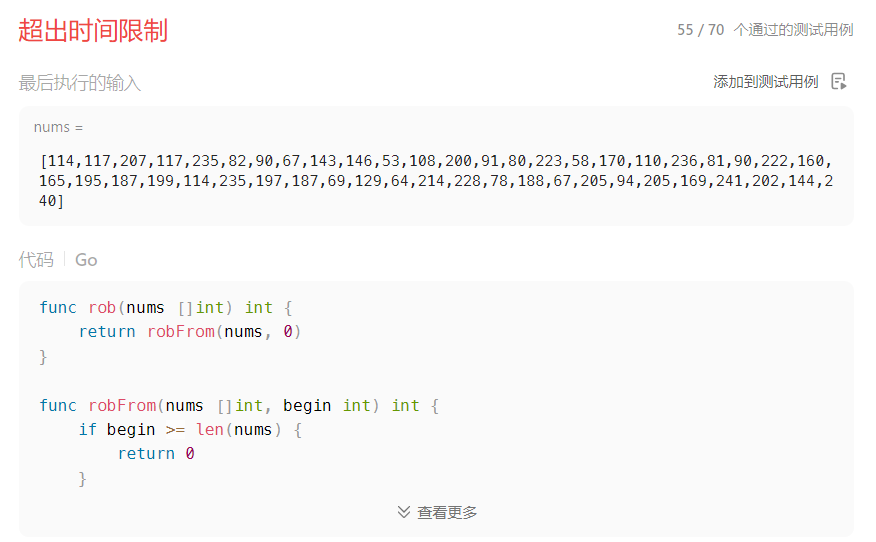
提交代码到官方后,提示 “测试超出时间限制”,说明代码的运行时间复杂度太高了,也就是代码运行时间存在优化空间。
超时原因分析
在尝试优化暴力搜索之前,我们先来分析一下刚才的算法为何时间复杂度很高。
对于每个房屋,我们都需要检测从其开始到最后一个房屋,可以偷窃到的最大金额,这会产生一个问题: 元素重复检测,也就是因为 “重叠子问题” 导致的 子问题重复计算。
举例来说,遇到第 1 个房屋 (index = 0) 时,在递归过程中会出现两种方案:
- 偷窃当前房屋,然后 (递归) 偷窃下下个 (第 3 个) 房屋 (index = 2)
- 不偷窃当前房屋,然后 (递归) 偷窃下个 (第 2 个) 房屋 (index = 1)
无论执行哪种方案,第 3 个房屋 (index = 2) 都会被重复检测,以此类推,随着递归的深度不断增加,重复检测的房屋会越来越多。
如图所示,重复检测的房屋使用相同的颜色进行标记。
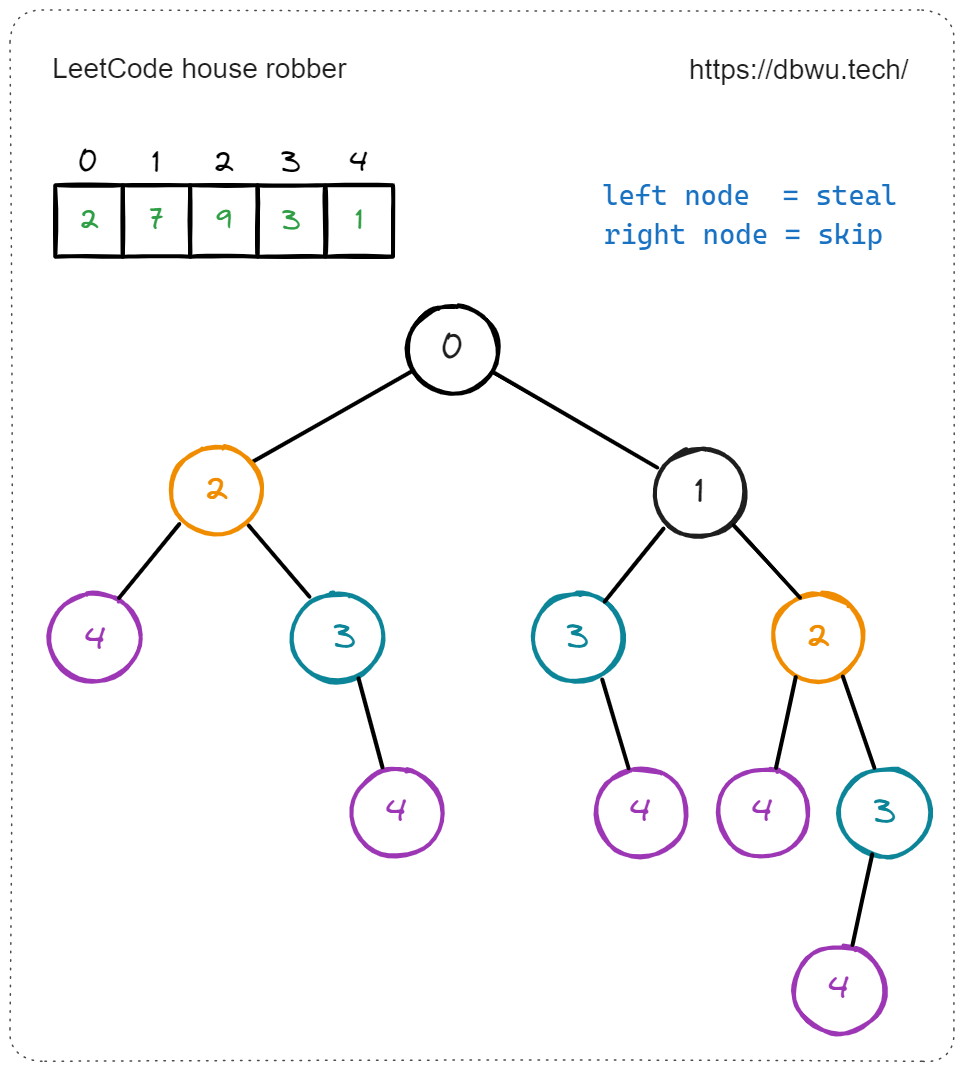
📝 记忆化搜索
现在我们已经分析出了暴力搜索的超时原因 (子问题重复计算),和 Fibonacci 问题类似,作为优化方案,可以采用一个 额外的备忘录 来记录已经检测过的元素组合,具体来说:
- 递归过程中,如果当前房屋已经检测过,直接返回备忘录中的金额即可
- 如果当前房屋未检测过,进行递归检测,并在递归结束后将对应的金额添加到备忘录中
下面是对应的实现代码:
// 记忆化: 避免重复计算
func robMemo(nums []int) int {
n := len(nums)
memo := make([]int, n)
// 备忘录金额初始化为 -1
for i := 0; i < n; i++ {
memo[i] = -1
}
return robFromMemo(nums, 0, &memo)
}
func robFromMemo(nums []int, begin int, memo *[]int) int {
if begin >= len(nums) {
return 0
}
if (*memo)[begin] != -1 {
return (*memo)[begin]
}
// 偷取当前房屋
// 偷取完当前房屋后,跳过下一个房屋,去偷下下一个房屋
steal := nums[begin] + robFrom(nums, begin+2)
// 不偷取当前房屋
// 去偷下一个房屋
skip := robFrom(nums, begin+1)
(*memo)[begin] = max(steal, skip)
// 返回两种偷取方案种的最大值
return max(steal, skip)
}
代码执行过程示例
如图所示,有了备忘录之后,每个元素组合只会被计算一次,计算量会大大减少。
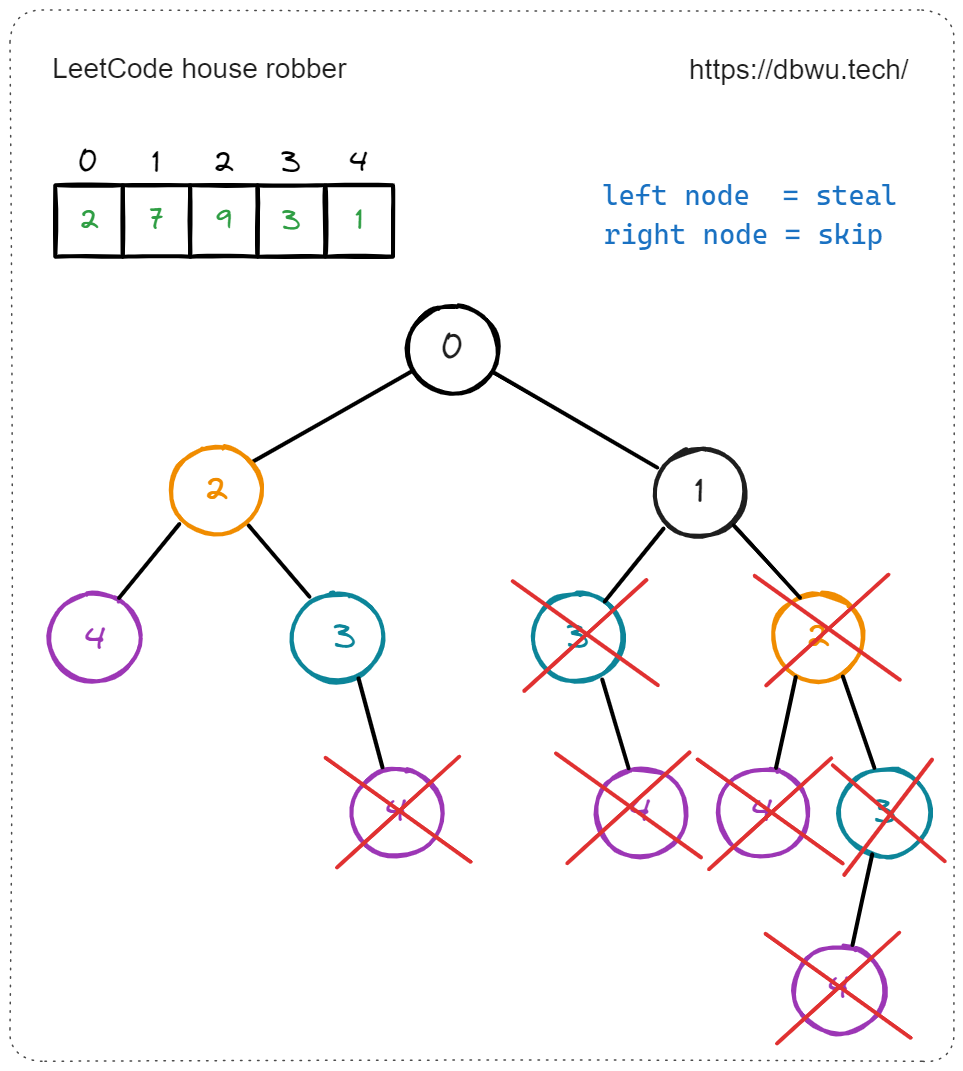
由于每个房屋只会被检测一次,所以算法的整体性能是非常高的,当然,因为备忘录使用了额外的内存空间,外加递归过程中产生的堆栈分配,使得内存占用提高很多,所以该记忆化搜索算法属于典型的 “空间换时间”。
🚀 动态规划
现在实现了暴力搜索和记忆化搜索代码之后,我们来思考如何编写动态规划代码。
状态转移方程
设计正确的状态转移方程是解决动态规划问题的前提。
和记忆化搜索一样,动态规划也通过存储中间结果来避免重复计算,但是动态规划采用循环迭代来实现,尝试从最小的问题开始,逐步构建问题的解。
自顶向下时,计算从当前房屋开始,到最后一个房屋,可以偷窃的最大金额
自底向上时,计算以当前房屋作为最后一个房屋,根据已有的状态结果,可以偷窃的最大金额
例如对于房屋 3 来说,其可以偷窃的最大金额为下列两个金额中的较大值:
- 偷窃房屋 3: 金额为房屋 1 和房屋 3 的金额之和
- 不偷窃房屋 2: 金额为房屋 2 的金额
根据这两个规则条件,可以推导出对应的状态转移方程,其中 F(i) 表示可以从第 i 个房屋中偷取到的最大金额,nums[i] 表示第 i 个房屋中的金额。
$$ \begin{align*} F(i) = \begin{cases} \max\ (F(i-2) + nums[i], F(i-1) ) \ & \text {,} \text{if i > 1} \\ \max\ (nums[1], nums[0] ) \ & \text {,} \text{if i == 1} \\ nums[0] \ & \text {,} \text{if i == 0} \end{cases} \end{align*} $$
实现代码
计算出状态转移方程之后,剩下的事情就是将算法步骤直接翻译为代码就可以了,下面的是动态规划的实现代码。
// 动态规划
func rob(nums []int) int {
n := len(nums)
if n == 0 {
return 1
}
if n == 1 {
return nums[0]
}
dp := make([]int, n)
dp[0] = nums[0]
dp[1] = max(dp[0], nums[1])
for i := 2; i < n; i++ {
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
}
return dp[n-1]
}
下面是动态规划代码的执行过程部分示例。
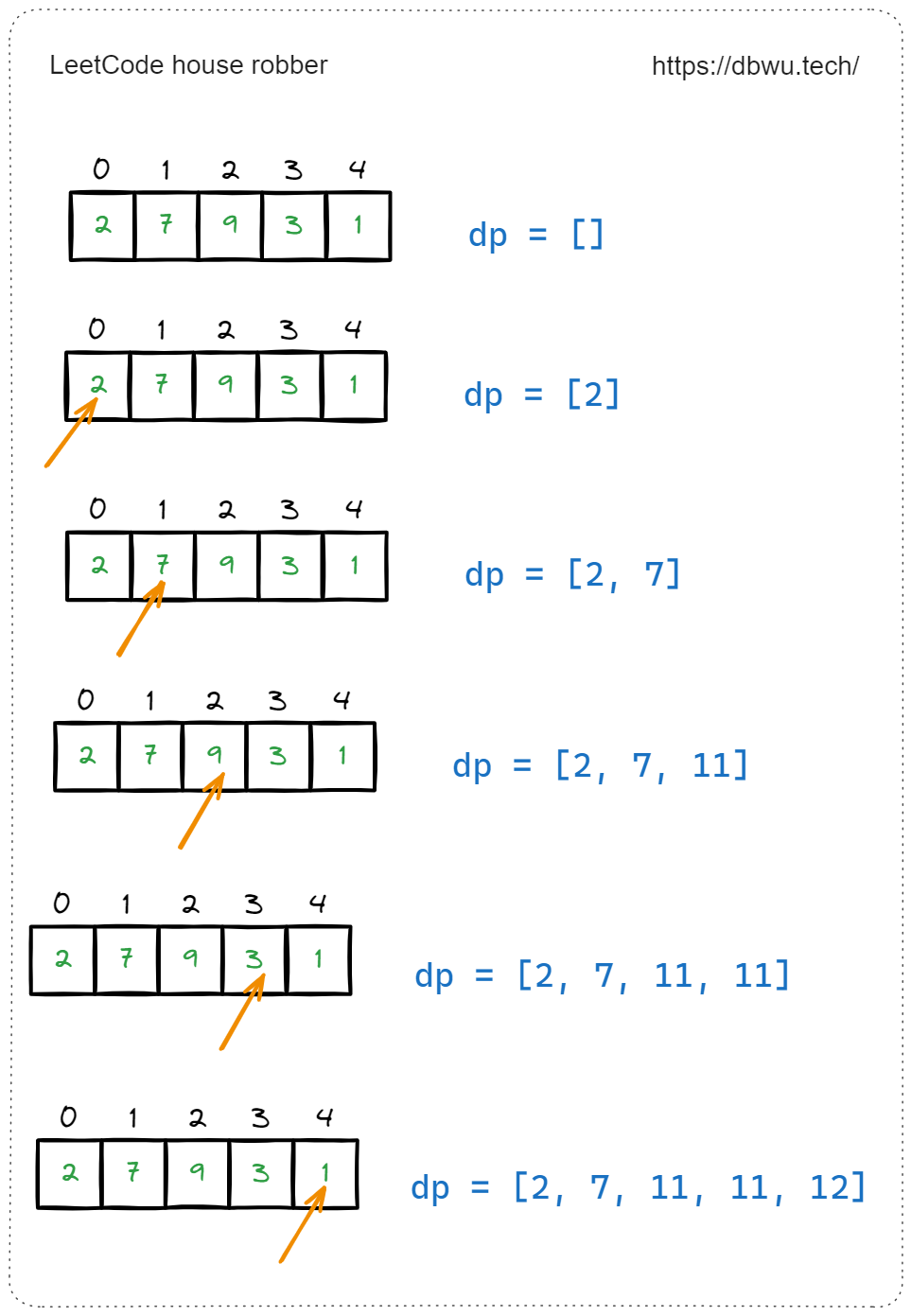
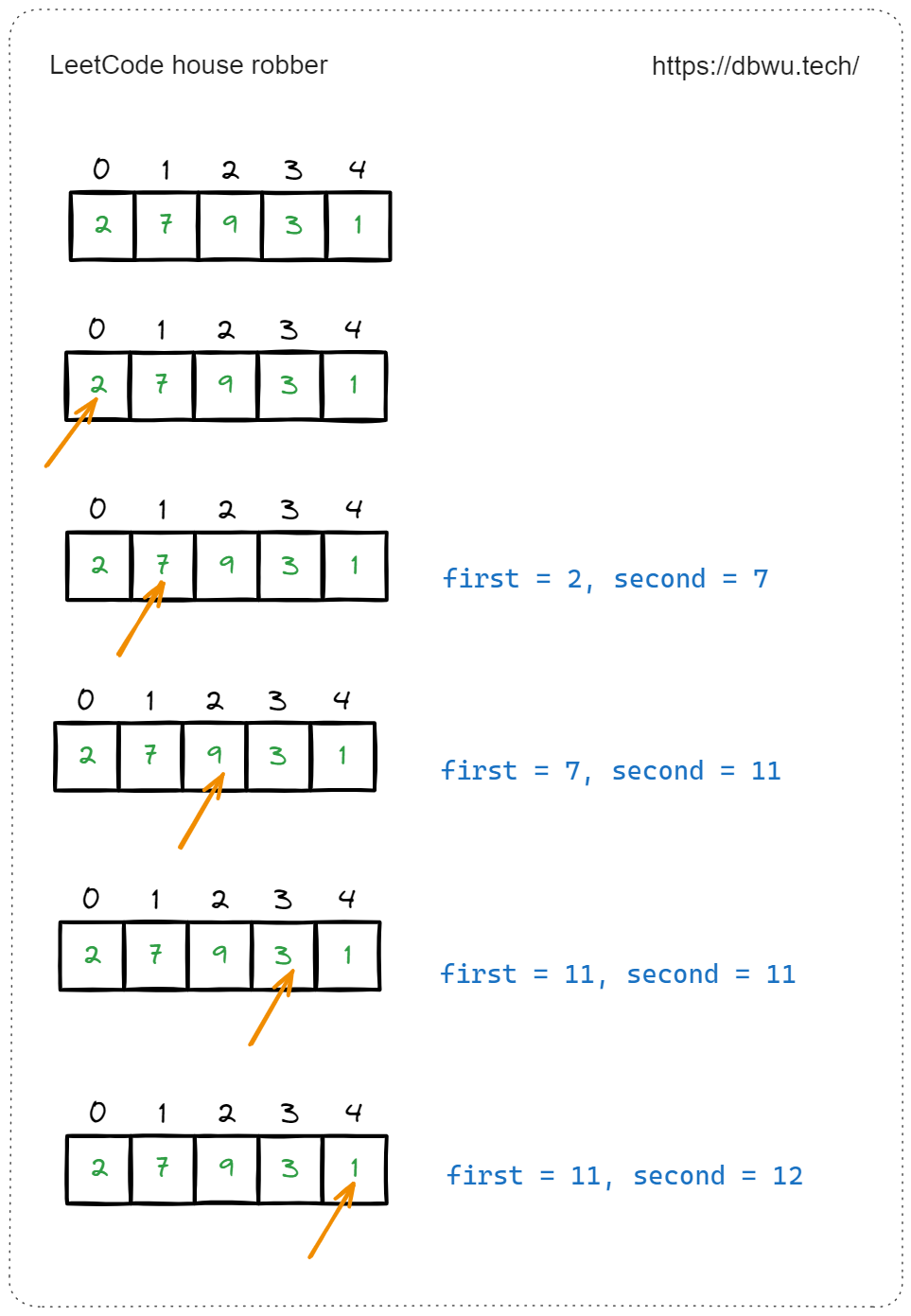
状态压缩优化
在刚才的动态规划实现代码中,虽然使用了一个数组来保存中间状态结果,但是最终返回数据时,只需要最后一个状态 (也就是到最后一个房屋时,可以偷窃的最大金额),而且在状态转换过程中,可以发现 F(i) 之和 F(i - 1), F(i - 2) 有关系,因此可以将状态数组压缩到两个变量 first, second 。
以当前房屋作为 “最后一个房屋” (相对位置)来说:
- first: 偷窃上上个房屋,可以得到的最大金额,也就是状态转移中的
F(i - 2) - second: 偷窃上个房屋,可以得到的最大金额,也就是状态转移中的
F(i - 1)
当检测完当前房屋之后,second 就变为了 “当前房屋”,first 就变成了 “上个房屋”,两个变量在遍历房屋的过程中 “滚动更新”,不断交替,最后返回 second 变量即可。
// 优化 DP 数组为两个滚动变量
func rob2(nums []int) int {
n := len(nums)
if n == 0 {
return 1
}
if n == 1 {
return nums[0]
}
first := nums[0]
second := max(first, nums[1])
for i := 2; i < n; i++ {
first, second = second, max(first+nums[i], second)
}
return second
}