动态规划简明教程 - 3
❓ 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
# 示例来自: https://leetcode.cn/
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
💡 解题过程
动态规划的子问题分解属于自顶向下的思想,因此在解题时可以按照 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 的顺序来实现代码,这样循序渐进地优化更符合我们的思考过程,也可以降低我们从一开始直接推导状态转移方程的心理压力。
接下来,我们先尝试着给出一个可行的题解,然后在这个基础上慢慢迭代优化。
解题方法函数原型:
func longestPalindrome(s string) string {}
单元测试
为了节省篇幅,这里给出针对本题的单元测试代码,不管 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 哪种实现方式,都可以直接运行该单元测试。
func Test_longestPalindrome(t *testing.T) {
type args struct {
s string
}
tests := []struct {
name string
args args
want string
}{
{
"test an empty string",
args{""},
"",
},
{
"test a single character string",
args{"a"},
"a",
},
{
"test a string that contains only one duplicate character",
args{"bbbbb"},
"bbbbb",
},
{
"No.1 test a string that contains multiple duplicate characters",
args{"bcabad"},
"aba",
},
{
"No.2 test a string that contains multiple duplicate characters",
args{"cbbd"},
"bb",
},
{
"No.3 test a string that contains multiple duplicate characters",
args{"abccbefg"},
"bccb",
},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := longestPalindrome(tt.args.s); got != tt.want {
t.Errorf("longestPalindrome() = %v, want %v", got, tt.want)
}
})
}
}
💪 暴力搜索
解题思路:
回文字符串的检测方式,可以单独写一个方法来实现,下面是一个简单的实现。
// 判断一个字符串是否为回文字符串
func isPalindrome(s string) bool {
n := len(s)
for i := 0; i < n>>1; i++ {
if s[i] != s[n-i-1] {
return false
}
}
return true
}
有了检测回文字符串的方法之后,我们可以按照如下思路来实现暴力搜索方法:
- 遍历字符串
- 以每个当前字符为起始位置
j,检测到字符串结尾可以形成的最大回文字符串长度j - i - 如果以当前字符开始可以形成更长的回文字符串,更新
已知的最大回文字符串长度 maxLen - 重复第 2, 3 步骤,直到计算到
s[i + maxLen], 后面的不需要再计算了,因为不可能形成比当前的maxLen更大的子回文字符串了
实现代码
根据解题思路,可以写出如下的代码:
// 题解代码
// 暴力解法(不会超时)
func longestPalindromeBruteForce(s string) string {
if len(s) <= 1 {
return s
}
res := ""
maxLen := 0
for i := 0; i < len(s); i++ {
// 从当前字符开始,直到字符串结尾
// 检测可以形成的最大回文字符串长度
for j := len(s); j > i+maxLen; j-- {
if isPalindrome(s[i:j]) && j-i > maxLen {
maxLen = j - i
res = s[i:j]
}
}
}
return res
}
// 判断一个字符串是否为回文字符串
func isPalindrome(s string) bool {
n := len(s)
for i := 0; i < n>>1; i++ {
if s[i] != s[n-i-1] {
return false
}
}
return true
}
提交超时 ?
运行单元测试:
$ go test -v -count=1 .
输出结果如下:
=== RUN Test_longestPalindrome
=== RUN Test_longestPalindrome/test_an_empty_string
=== RUN Test_longestPalindrome/test_a_single_character_string
=== RUN Test_longestPalindrome/test_a_string_that_contains_only_one_duplicate_character
=== RUN Test_longestPalindrome/No.1_test_a_string_that_contains_multiple_duplicate_characters
=== RUN Test_longestPalindrome/No.2_test_a_string_that_contains_multiple_duplicate_characters
=== RUN Test_longestPalindrome/No.3_test_a_string_that_contains_multiple_duplicate_characters
--- PASS: Test_longestPalindrome (0.00s)
--- PASS: Test_longestPalindrome/test_an_empty_string (0.00s)
--- PASS: Test_longestPalindrome/test_a_single_character_string (0.00s)
--- PASS: Test_longestPalindrome/test_a_string_that_contains_only_one_duplicate_character (0.00s)
--- PASS: Test_longestPalindrome/No.1_test_a_string_that_contains_multiple_duplicate_characters (0.00s)
--- PASS: Test_longestPalindrome/No.2_test_a_string_that_contains_multiple_duplicate_characters (0.00s)
--- PASS: Test_longestPalindrome/No.3_test_a_string_that_contains_multiple_duplicate_characters (0.00s)
PASS
ok leetcode/0005.Longest-Palindromic-Substring 0.002s
单元测试全部通过,表面上来看,我们的暴力搜索实现没有问题,现在去官方提交看看运行结果。
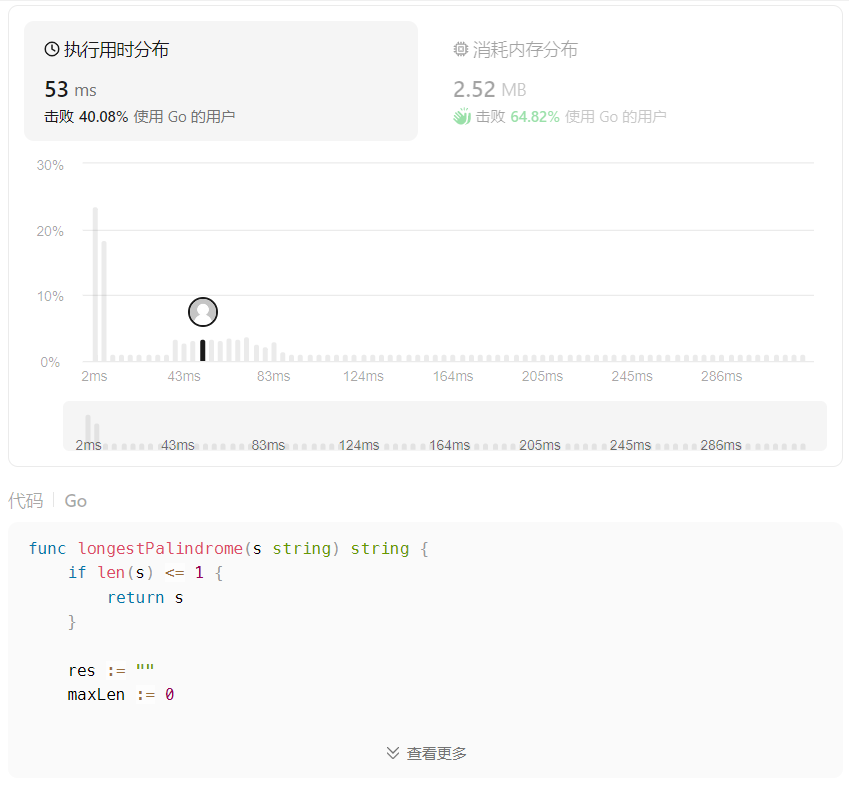
提交代码到官方后,暴力算法居然通过了 (可能是官方没有提供足够的复杂测试?),接下来,我们来分析一下,暴力搜索代码运行时间是否存在优化空间。
📝 记忆化搜索
有了前面几篇文章的基础,我们可以直接将暴力搜索改造为记忆化搜索。
下面是对应的实现代码:
// 记忆化搜索
func longestPalindromeMemo(s string) string {
n := len(s)
if n <= 1 {
return s
}
res := ""
maxLen := 0
// -1: 初始状态
// 0: 表示 s[i:j] 不是回文串
// 1: 表示 s[i:j] 是回文串
memo := make([][]int, n)
for i := range memo {
memo[i] = make([]int, n)
for j := range memo[i] {
memo[i][j] = -1
}
}
for i := 0; i < n; i++ {
for j := len(s); j > i+maxLen; j-- {
if isPalindromeMemo(s, i, j-1, memo) > 0 && j-i > maxLen {
maxLen = j - i
res = s[i:j]
}
}
}
return res
}
// 记忆化检测回文字符串
func isPalindromeMemo(s string, i, j int, memo [][]int) int {
if i == j {
return 1
}
if memo[i][j] != -1 {
// 代码不会执行到这里
return memo[i][j]
}
// 默认 s[i:j] 不是回文字符串
memo[i][j] = 0
if s[i] == s[j] && (j-i <= 1 || isPalindromeMemo(s, i+1, j-1, memo) > 0) {
memo[i][j] = 1
}
return memo[i][j]
}
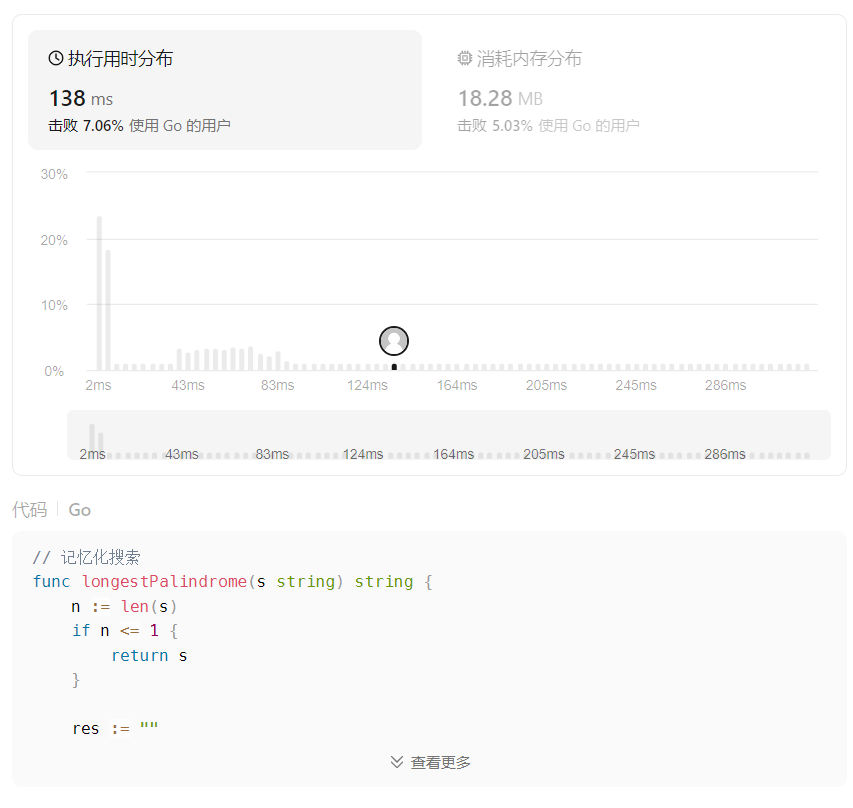
性能变慢分析
通过暴力搜索和记忆化搜索提交后的代码执行时间分析,记忆化搜索并没有像预期中的提升性能,反而下降了很多,问题出在了哪里呢?
简单分析一下记忆化搜索的递归过程,我们会发现,每次调用 (包括递归调用) isPalindromeMemo() 方法时,参数 i 和 j 都是不同的,也就是说,虽然加了备忘录,但是根本没用到,反而因为备忘录使用了多余的内存和方法递归调用,导致代码的执行性能降低了。
举例来说,当计算字符串第一个元素 s[0] 时,会分别递归计算 s[0] -> s[1:n],执行过程如图所示:
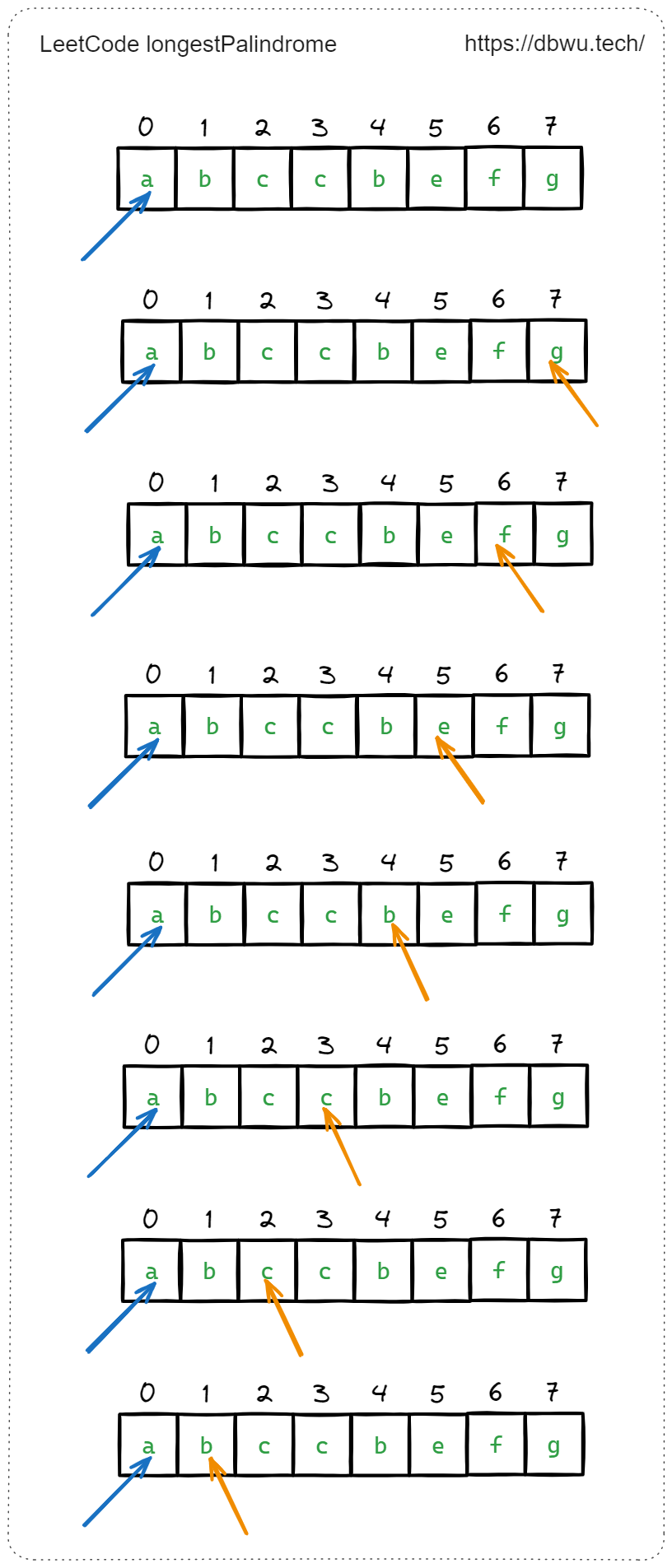
同理,当执行到第二个元素 s[0] 时,还是会分别递归计算 s[1] -> s[1:n],以此类推,直到计算到 s[i + maxLen], 后面的不需要再计算了,因为不可能形成比当前的 maxLen 更大的子回文字符串了。
🚀 动态规划
现在实现了暴力搜索和记忆化搜索代码之后,我们来思考如何编写动态规划代码。
状态转移方程
设计正确的状态转移方程是解决动态规划问题的前提。
根据回文串的定义,对于一个长度大于 2 的回文子串来说,将其首尾字符去掉之后,其仍然是一个回文串。例如回文串 ababa,首尾字符去掉之后变为 bab,仍然是一个回文串。
反过来说,对于一个已知的长度大于 2 的回文串,如果在其首尾加两个相同的字符,其会构成一个新的回文串。例如回文串 bab,首尾加上字符 a 变为 ababa,变成了一个新的回文串。
根据这两个规则条件,可以推导出针对长度大于 2 的回文串的状态转移方程,其中 F(i, j) 表示字符串 s[i..j] 是否是回文串。
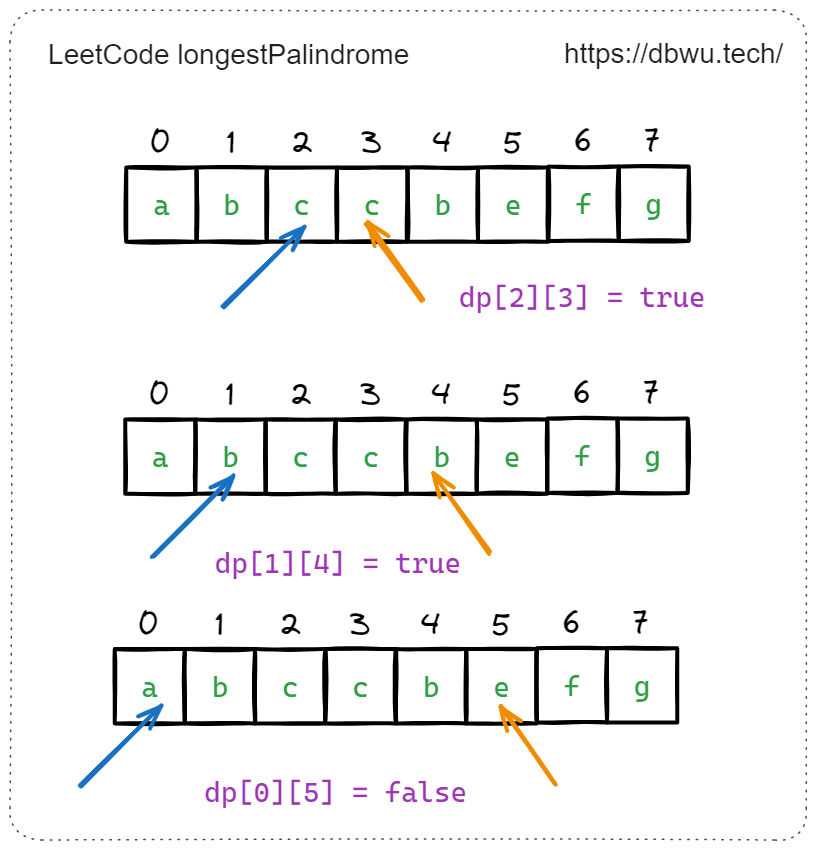
对应的状态转移方程如下:
$$ \begin{align*} \ F(i, j) = F(i+1, j-1) \ & \text {, } \text{if }s[i] == s[j] \ \end{align*} $$
那么对于长度小于 2 的字符串 (边界条件),又该如何处理呢?
- 长度为 0 或长度为 1,
F(i, i)是回文串 - 长度为 2, 如果
s[i] == s[i+1],F(i, i+1)是回文串
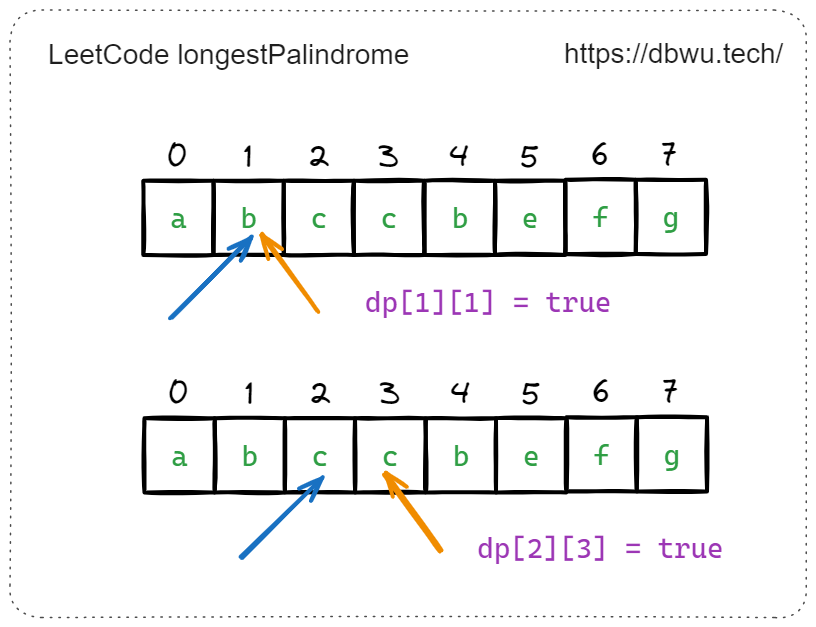
对应的状态转移方程如下:
$$ \begin{align*} \begin{cases} \ F(i, i) = true \ & \text { } \text{ } \\ \ F(i, i+1) = true \ & \text { } \text{if }s[i] == s[i+1] \end{cases} \end{align*} $$
根据这两个示例和边界条件,最后合并为如下的状态转移方程:
$$ \begin{align*} \begin{cases} \ F(i, i) = true \ & \text {, } \text{default } \\ \ F(i, i+1) = true \ & \text {, } \text{if }s[i] == s[i+1] \\ \ F(i, j) = F(i+1, j-1) \ & \text {, } \text{if }s[i] == s[j] \end{cases} \end{align*} $$
算法步骤
根据上面的分析过程和状态转移过程,可以得到如下的算法步骤:
- 定义问题状态:计算子字符串
s[i..j]是否是回文串 - 状态转移方程:如前文所示
- 初始化:建立状态转移表 (一个二维数组),所有长度为 1 的子串都是回文串
- 计算子问题:计算从当前字符开始,每次递增 1,单次可以形成的最大回文串 (向右扩展)
- 计算原问题:计算从当前字符开始,可以形成的最大回文串,同时更新当前已知的最大回文串长度
实现代码
计算出状态转移方程之后,剩下的事情就是将算法步骤直接翻译为代码就可以了,下面的是动态规划的实现代码。
// 动态规划
func longestPalindromeDP(s string) string {
n := len(s)
if n <= 1 {
return s
}
// 最大回文起始位置
begin := 0
// 最大回文长度, 通过起始位置+长度, 可以直接返回结果
maxLen := 1
// dp[i][j] 表示 s[i..j] 是否是回文串
dp := [][]bool{}
for i := 0; i < n; i++ {
dp = append(dp, make([]bool, n))
}
// 初始化:所有长度为 1 的子串都是回文串
for i := 0; i < n; i++ {
dp[i][i] = true
}
// 递推开始
// 先枚举子串长度
for left := 2; left <= n; left++ {
// 枚举左边界
for i := 0; i < n; i++ {
// 由 left 和 i 可以确定右边界,即 j - i + 1 = left
j := left + i - 1
if j >= n {
break
}
if s[i] != s[j] {
dp[i][j] = false
} else {
// 边界情况, "aa" "aba" ...
if j-i < 3 {
dp[i][j] = true
} else {
dp[i][j] = dp[i+1][j-1]
}
}
// 只要 dp[i][j] == true 成立,就表示子串 s[i..j] 是回文
// 更新最大回文长度和最大回文起始位置
if dp[i][j] && j-i+1 > maxLen {
begin = i
maxLen = j - i + 1
}
}
}
return s[begin : begin+maxLen]
}
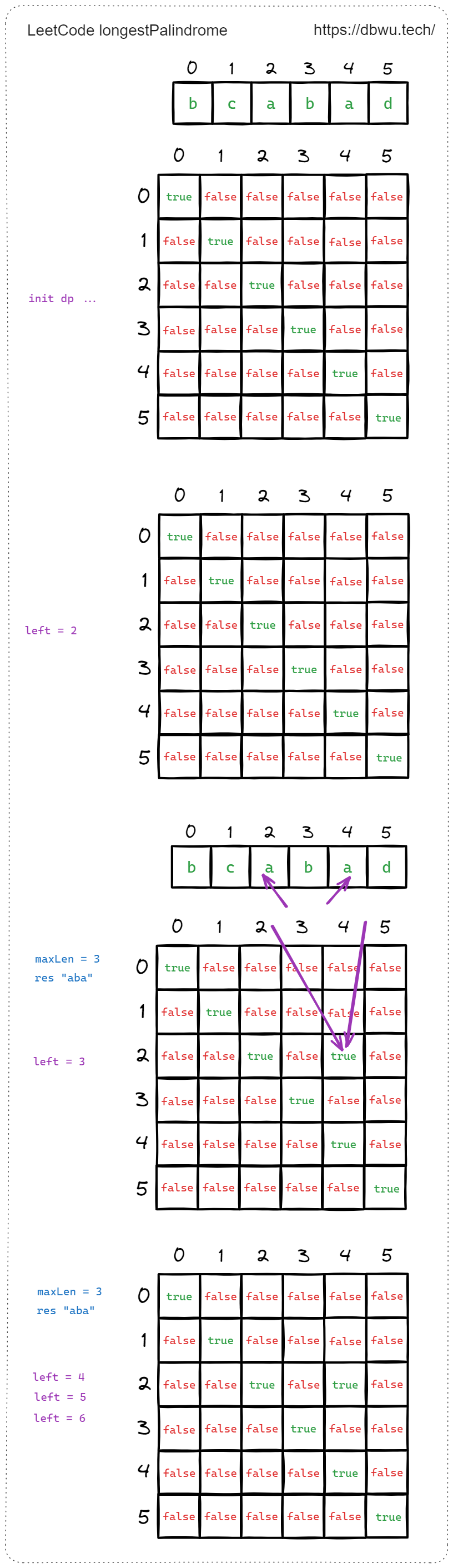
下面是动态规划代码的执行过程部分示例。