动态规划简明教程 - 5
❓ 最大正方形
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
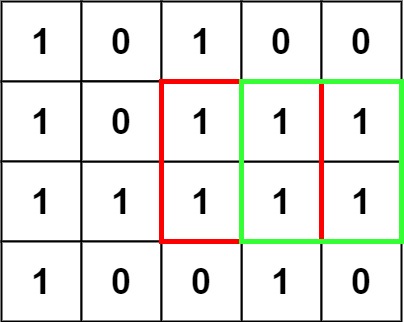
如图所示的的矩阵中,最大正方形面积为 4。
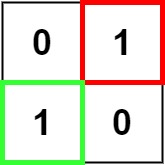
如图所示的的矩阵中,最大正方形面积为 1。
💡 解题过程
动态规划的子问题分解属于自顶向下的思想,因此在解题时可以按照 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 的顺序来实现代码,这样循序渐进地优化更符合我们的思考过程,也可以降低我们从一开始直接推导状态转移方程的心理压力。
接下来,我们先尝试着给出一个可行的题解,然后在这个基础上慢慢迭代优化。
解题方法函数原型:
func maximalSquare(matrix [][]byte) int {}
单元测试
为了节省篇幅,这里给出针对本题的单元测试代码,不管 暴力搜索 -> 记忆化搜索 -> 动态规划搜索 哪种实现方式,都可以直接运行该单元测试。
func Test_maximalSquare(t *testing.T) {
type args struct {
matrix [][]byte
}
tests := []struct {
name string
args args
want int
}{
{
"test-1",
args{nil},
0,
},
{
"test-2",
args{[][]byte{
{'0'},
}},
0,
},
{
"test-3",
args{[][]byte{
{'1'},
}},
1,
},
{
"test-4",
args{[][]byte{
{'0', '1'},
{'1', '0'},
}},
1,
},
{
"test-5",
args{[][]byte{
{'1', '1'},
{'1', '1'},
}},
4,
},
{
"test-6",
args{[][]byte{
{'1', '0', '1', '0', '0'},
{'1', '0', '1', '1', '1'},
{'1', '1', '1', '1', '1'},
{'1', '0', '0', '1', '0'},
}},
4,
},
}
for _, tt := range tests {
t.Run(tt.name, func(t *testing.T) {
if got := maximalSquare(tt.args.matrix); got != tt.want {
t.Errorf("maximalSquare() = %v, want %v", got, tt.want)
}
})
}
}
💪 暴力搜索
解题思路:
正方形的特征为四条边长度相等,所以一个最简单可行的方案为:
- 从矩阵左上角开始、到右下角结束、逐个元素遍历搜索 (也就是矩阵的逐行逐列遍历)
- 以当前元素作为待检测正方形的左上角开始检测
- 边长初始化为 1
- 如果以当前元素作为正方形左上角、当前边长为正方形边长可以形成的 “新的正方形” 中的元素全部为 1,当前边长 + 1
- 重复第 3, 4 步,直到 “新的正方形” 中的元素包含 0
- 更新已知的最大正方形面积
- 开始遍历矩阵的下一个元素
- 重复第 1 - 7 步,直到遍历到矩阵的最后一个元素 (右下角元素)
暴力搜索示例
首先,我们从矩阵 (二维数组) 的左上角开始遍历,按照从左到右、从上到下的顺序,一直遍历到矩阵的最后一个元素。
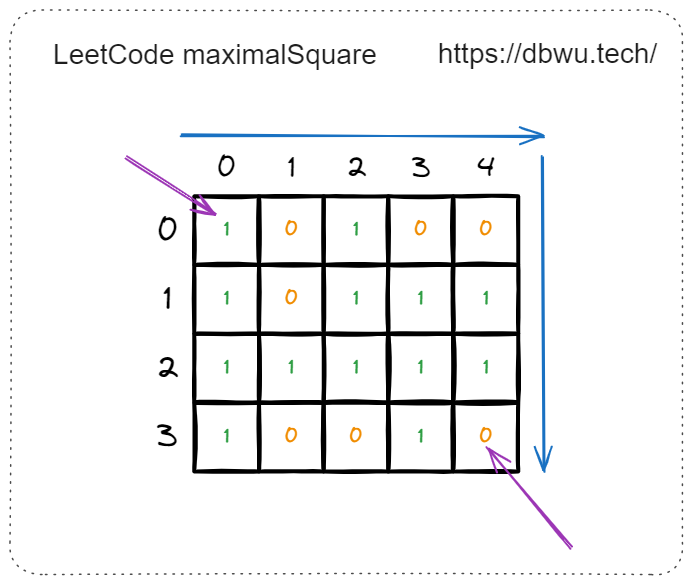
遍历到任意一个元素时,如果当前元素为 0, 直接跳过 (因为 0 无法构成有效正方形),如果当前元素为 1, 我们就以当前元素为 “新的正方形” 的左上角,不断递增边长,试图寻找面积更大的正方形。
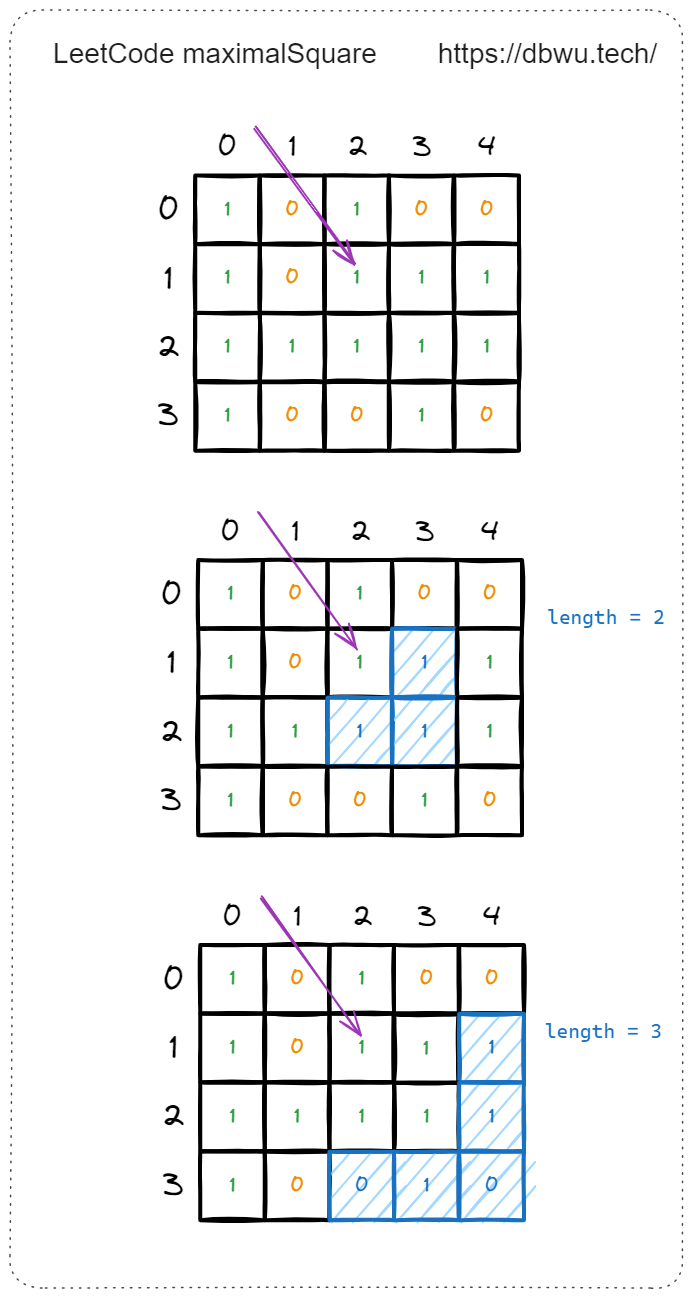
例如遍历到矩阵中坐标为 [1, 2] 的元素时,就以 [1, 2] 这个坐标作为 “新的正方形” 的左上角开始寻找:
Tips: 每次试图寻找面积更大的正方形时,只需要检测右侧的元素和底侧的元素,也就是当前正方形的外层元素,因为内层元素已经确认过了。
实现代码
根据解题思路,可以写出如下的代码:
// 题解代码
// 暴力搜索迭代版本 (超时)
// 超时原因: 重复检测
func maximalSquare(matrix [][]byte) int {
if len(matrix) == 0 {
return 0
}
var maxSide int
rows, cols := len(matrix), len(matrix[0])
// 按照矩阵逐个元素遍历
for i := 0; i < rows; i++ {
for j := 0; j < cols; j++ {
if matrix[i][j] == '0' {
continue
}
// 以当前坐标作为矩形左上角,检测最大正方形的边长
// 更新已知的最大正方形面积
maxSide = max(maxSide, search(matrix, i, j))
}
}
return maxSide * maxSide
}
// 搜索以当前坐标为最上角的最大正方形边长
func search(matrix [][]byte, x, y int) int {
rows, cols := len(matrix), len(matrix[0])
curSide := 1
// 边长从 2 开始递增
for length := 2; x+length <= rows && y+length <= cols; length++ {
for i := 0; i < length; i++ {
// 如果当前 “新的正方形” 中右侧的元素包含 0
// 直接返回对应的边长
if matrix[x+i][y+curSide] == '0' {
return curSide
}
}
for i := 0; i < length; i++ {
// 如果当前 “新的正方形” 中底侧的元素包含 0
// 直接返回对应的边长
if matrix[x+curSide][y+i] == '0' {
return curSide
}
}
curSide = length
}
return curSide
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
提交超时
运行单元测试:
$ go test -v -count=1 .
输出结果如下:
=== RUN Test_maximalSquare
=== RUN Test_maximalSquare/test-1
=== RUN Test_maximalSquare/test-2
=== RUN Test_maximalSquare/test-3
=== RUN Test_maximalSquare/test-4
=== RUN Test_maximalSquare/test-5
=== RUN Test_maximalSquare/test-6
--- PASS: Test_maximalSquare (0.00s)
--- PASS: Test_maximalSquare/test-1 (0.00s)
--- PASS: Test_maximalSquare/test-2 (0.00s)
--- PASS: Test_maximalSquare/test-3 (0.00s)
--- PASS: Test_maximalSquare/test-4 (0.00s)
--- PASS: Test_maximalSquare/test-5 (0.00s)
--- PASS: Test_maximalSquare/test-6 (0.00s)
PASS
ok leetcode/0221-Maximal-Square 0.002s
单元测试全部通过,表面上来看,我们的暴力搜索实现没有问题,现在去官方提交看看运行结果。
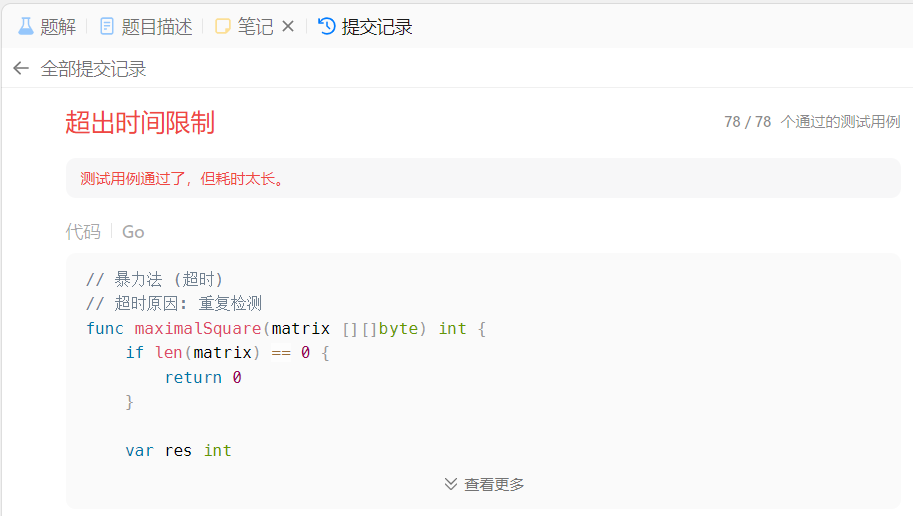
提交代码到官方后,给出的提示很明确:“测试用例通过了,但是耗时太长”,说明我们的算法实现是没有问题的,但是运行太慢了,说明代码的运行时间复杂度太高了,换句话说就是,代码运行时间存在优化空间。
超时原因分析
在尝试优化暴力搜索之前,我们先来分析一下刚才的算法为何时间复杂度很高。
例如遍历到矩阵中坐标为 [1, 2] 的元素时,边长从 2 开始递增,开始检测当前元素是否可以形成边长为 2 的 “新正方形” 。
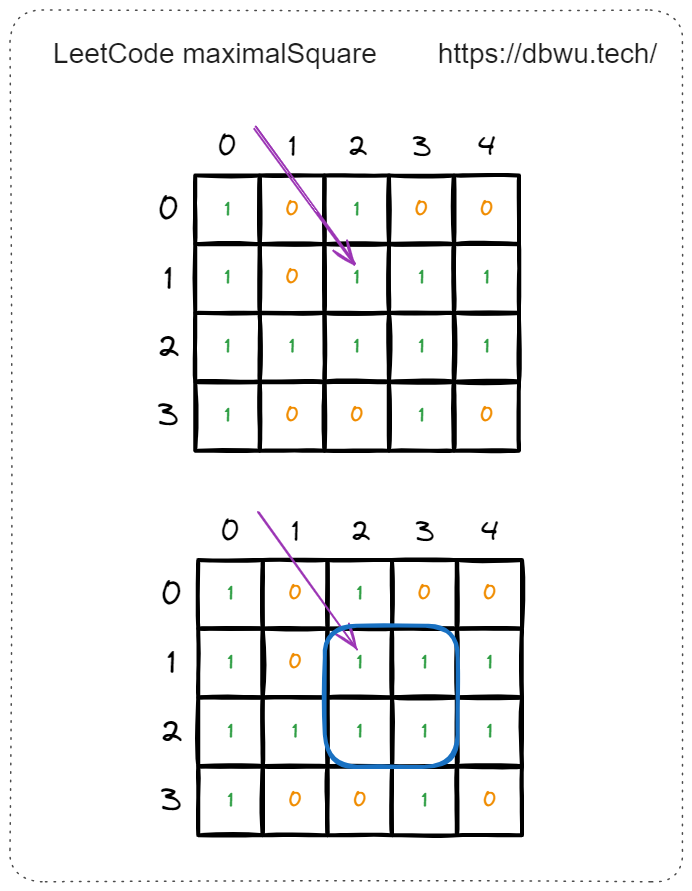
如图所示,边长为 2 时,可以形成的新的正方形,将变长递增到 3。
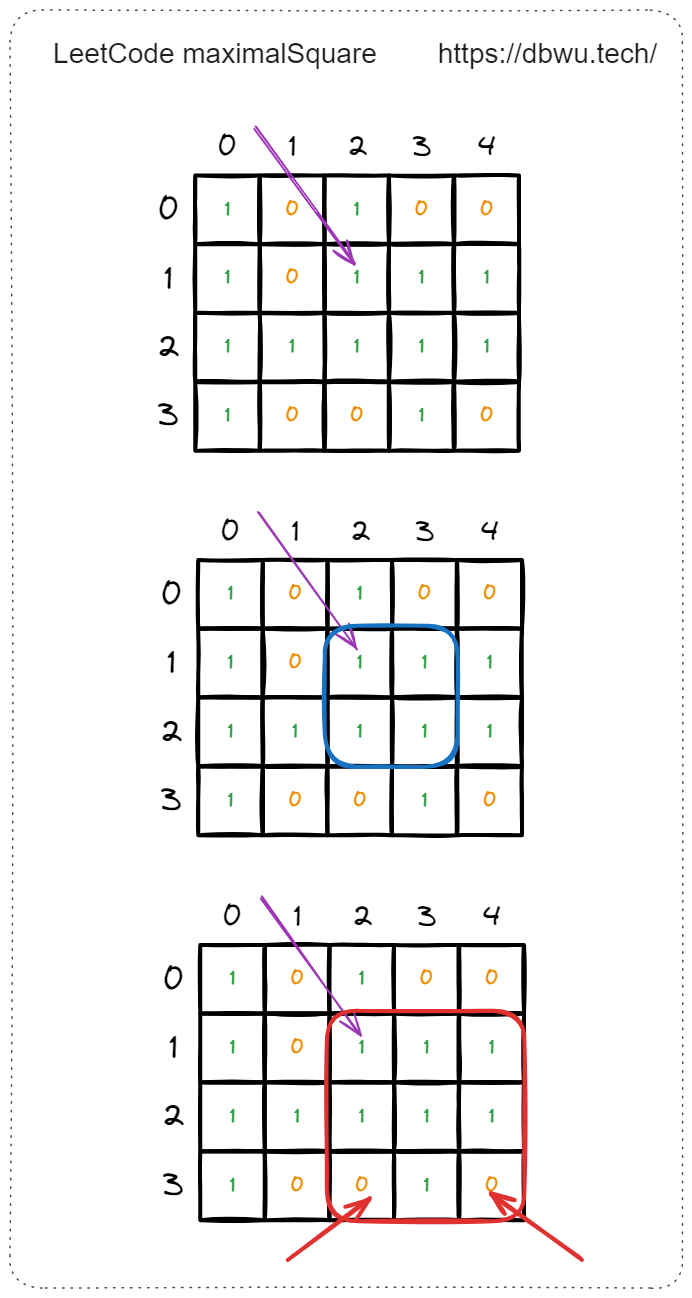
如图所示,边长为 3 时,无法形成的新的正方形,因为坐标 [3, 2] 和 坐标 [3, 4] 的元素值为 0。
到这里,坐标为 [1, 2] 的元素就检测完了 (最大正方形面积为 4),接下来开始检测下一个元素,坐标为 [1, 3] 的元素,从边长 2 开始检测。
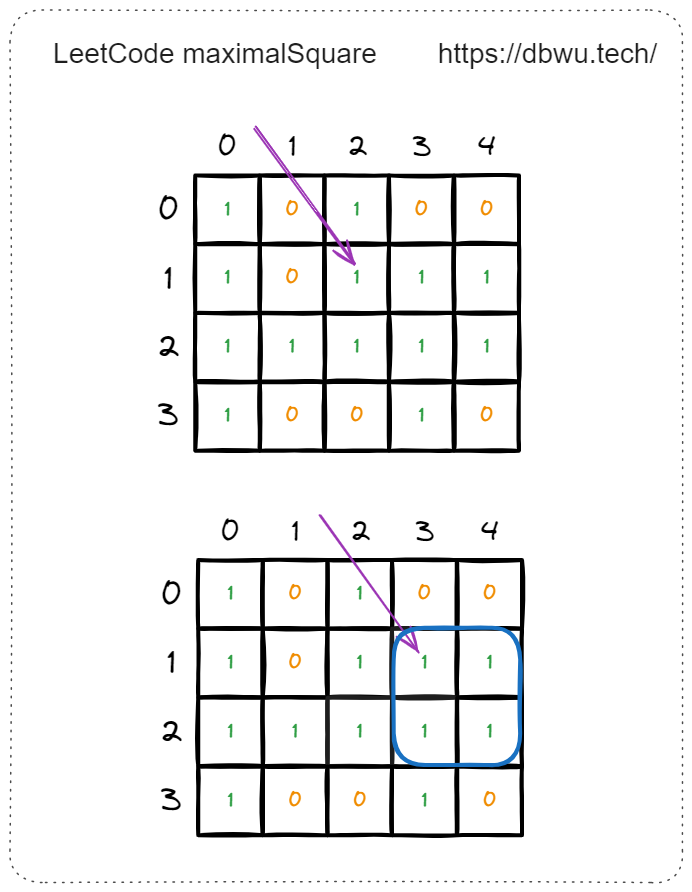
边长为 2 时,坐标为 [1, 3] 的元素时形成的 “新正方形” 的 4 个坐标为: [1, 3] [1, 4] [2, 3] [2, 4],仔细观察你会发现,这 4 个 坐标在检测上一个坐标 [1, 2] 元素时已经检测过了。
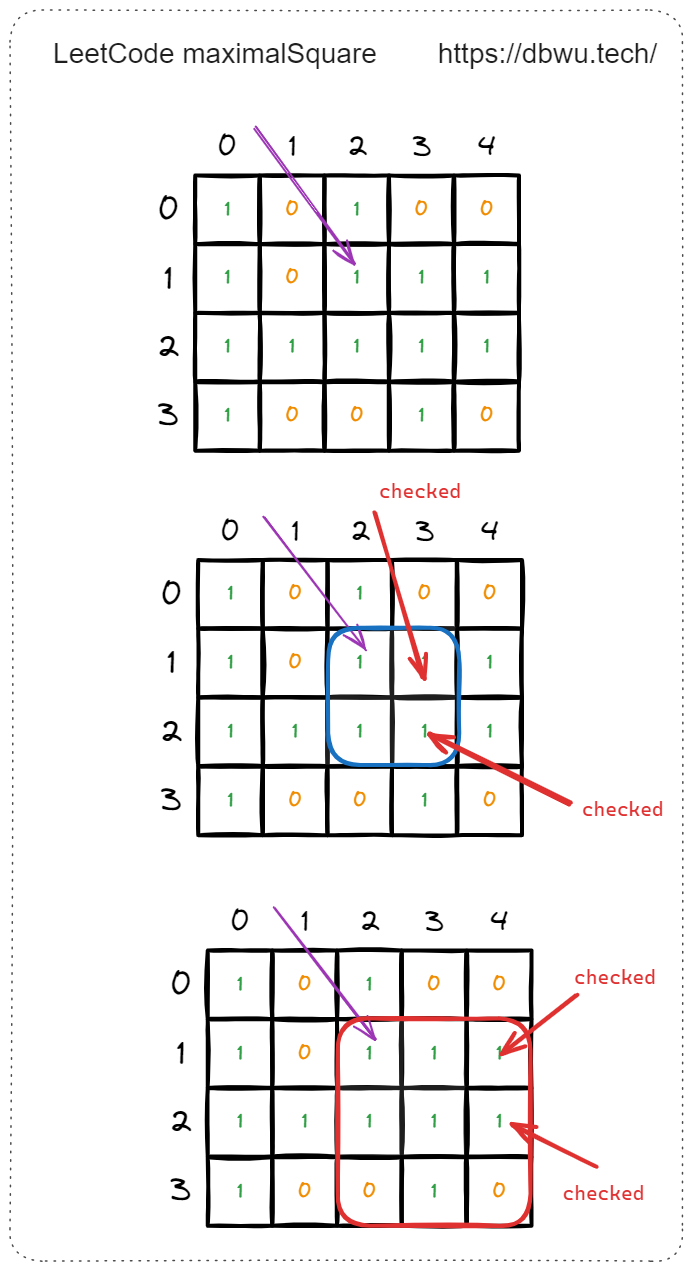
到了这里,代码超时的原因终于找到了: 元素重复检测,也就是因为 “重叠子问题” 导致的 子问题重复计算。
递归代码
下面是暴力搜索的递归版本实现代码,和迭代版本代码一样,提交后也会提示执行超时。

// 暴力搜索递归版本 (超时)
// 超时原因: 重复检测
func maximalSquare(matrix [][]byte) int {
if len(matrix) == 0 {
return 0
}
m, n := len(matrix), len(matrix[0])
maxSide := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
maxSide = max(maxSide, searchRecursive(matrix, i, j))
}
}
return maxSide * maxSide
}
// 搜索以当前坐标 [x, y] 为左上角的最大正方形边长
func searchRecursive(matrix [][]byte, x, y int) int {
if x >= len(matrix) || y >= len(matrix[0]) {
return 0
}
if matrix[x][y] == '0' {
return 0
}
// 搜索以 [当前坐标的底侧元素] 为坐标 的最大正常形边长
down := searchRecursive(matrix, x+1, y)
// 搜索以 [当前坐标的右侧元素] 为坐标 的最大正常形边长
right := searchRecursive(matrix, x, y+1)
// 搜索以 [当前坐标的右下侧元素] 为坐标 的最大正常形边长
diag := searchRecursive(matrix, x+1, y+1)
return 1 + min(down, right, diag)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(x, y, z int) int {
if x < y && x < z {
return x
}
if y < z {
return y
}
return z
}
📝 记忆化搜索
现在我们已经分析出了暴力搜索的超时原因 (子问题重复计算),作为优化方案,可以采用一个 额外的备忘录 来记录每个坐标的最大边长,具体来说:
- 遍历每个坐标元素时,需要分别计算该坐标的
底侧坐标、右侧坐标、右下侧坐标三个坐标为左上角时,可以形成的最大正方形边长 - 递归过程中:
- 对于当前坐标,如果备忘录中已经包含其最大正方形边长,直接返回
- 对于当前坐标,记录其可以形成的最大正方形边长到备忘录中
下面是对应的实现代码:
// 记忆化搜索
func maximalSquare(matrix [][]byte) int {
if len(matrix) == 0 {
return 0
}
m, n := len(matrix), len(matrix[0])
memo := make([][]int, m)
for i := range memo {
memo[i] = make([]int, n)
}
maxSide := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
maxSide = max(maxSide, searchMemo(matrix, i, j, memo))
}
}
return maxSide * maxSide
}
func searchMemo(matrix [][]byte, x, y int, memo [][]int) int {
if x >= len(matrix) || y >= len(matrix[0]) {
return 0
}
if matrix[x][y] == '0' {
return 0
}
// 如果备忘录中已经包含 [当前坐标] 的边长
// 直接返回
if memo[x][y] != 0 {
return memo[x][y]
}
// 搜索以 [当前坐标的底侧元素] 为坐标 的最大正常形边长
down := searchMemo(matrix, x+1, y, memo)
// 搜索以 [当前坐标的右侧元素] 为坐标 的最大正常形边长
right := searchMemo(matrix, x, y+1, memo)
// 搜索以 [当前坐标的右下侧元素] 为坐标 的最大正常形边长
diag := searchMemo(matrix, x+1, y+1, memo)
// 更新备忘录中 [当前坐标] 的边长
memo[x][y] = 1 + min(down, right, diag)
return memo[x][y]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(x, y, z int) int {
if x < y && x < z {
return x
}
if y < z {
return y
}
return z
}
代码执行过程示例
有了备忘录之后,每个坐标只会被计算一次,计算量会大大减少。
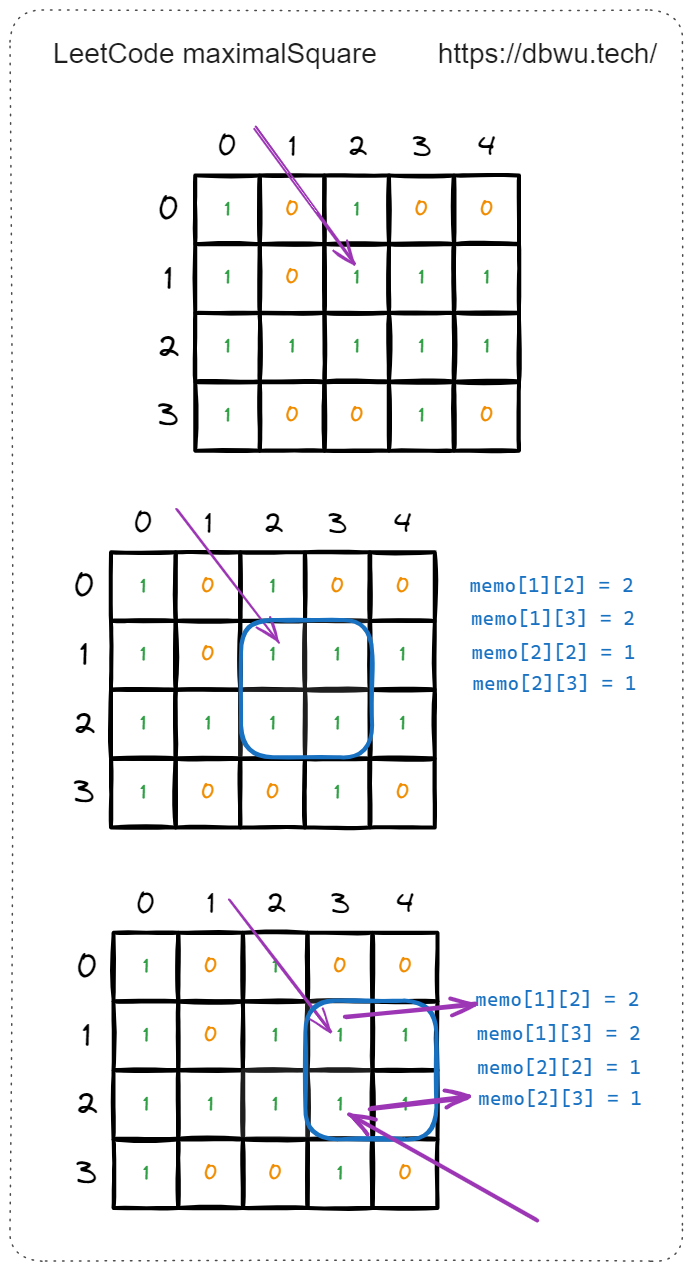
举例来说,当递归计算坐标 [1, 2] 时,会计算出其相邻的 4 个坐标可以形成的最大正方形并记录在备忘录中,当后续遍历到作标 [1, 3] 和坐标 [2, 3] 时,就不需要再次计算了,直接返回已有的备忘录中的值 (边长) 即可。
🚀 动态规划
现在实现了暴力搜索和记忆化搜索代码之后,我们来思考如何编写动态规划代码。
状态转移方程
设计正确的状态转移方程是解决动态规划问题的前提。
和前文中暴力搜索和记忆化搜索的 自顶向下 的实现不同,对于动态规划,我们考虑如何 自定向上 的实现。
自顶向下时,当前元素作为 “新的正方形” 左上角
自底向上时,当前元素作为 “新的正方形” 右下角 (和自顶向下正好相反,形成镜像)
遍历矩阵元素时,对应每个当前元素,如果确定其可以构成的最大正方形面积呢?既然当前元素是作为 “新的正方形” 的右下角,那么只要需要计算出其 上侧,左侧、左上角 的正方形边长,然后取三者中的最小值,最后加一 (当前元素的边长),就是当前元素可以构成的最大正方形边长。
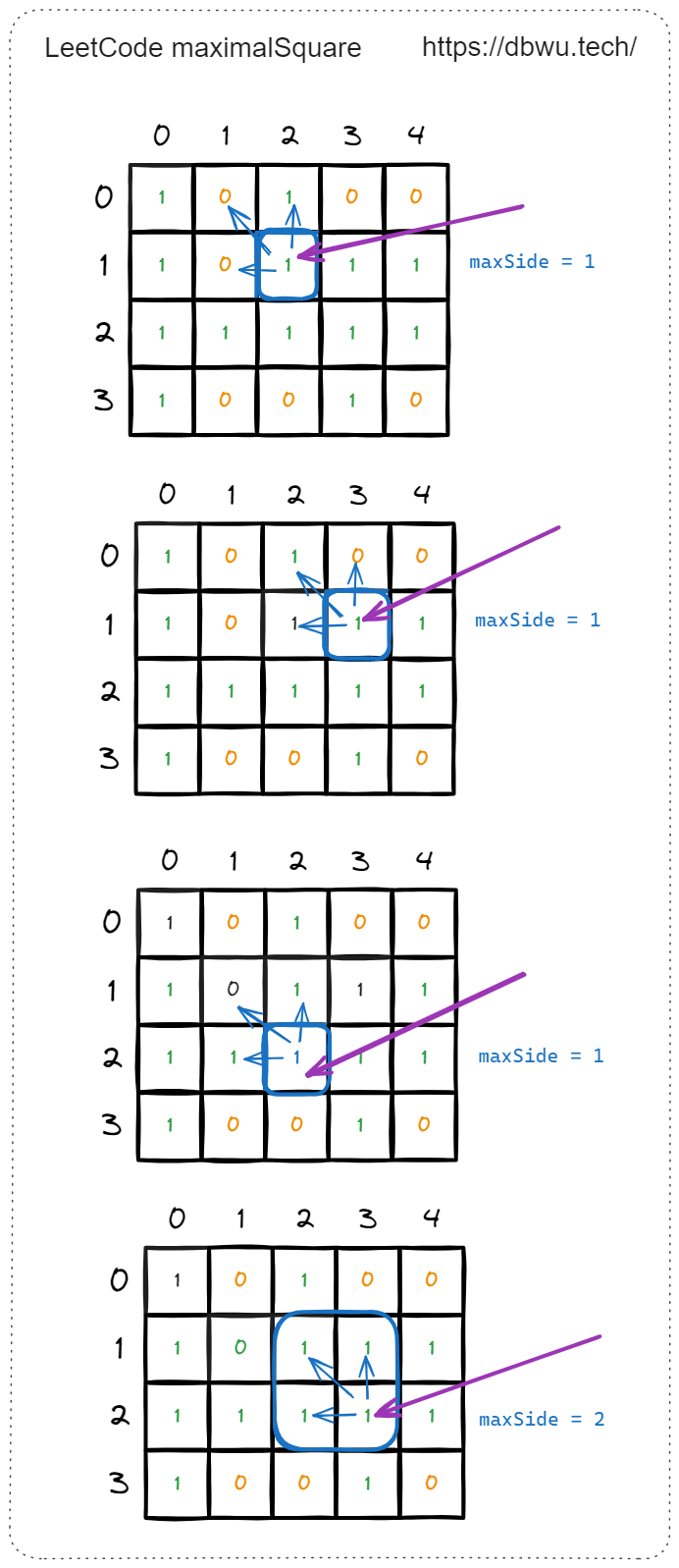
举例来说,当计算坐标 [1, 2] 时,只要需要计算出其 上侧,左侧、左上角 的正方形边长:
- 上侧: [0, 2], 可以构成的最大正方形边长 = 0
- 左侧: [1, 1], 可以构成的最大正方形边长 = 0
- 左上角: [0, 1], 可以构成的最大正方形边长 = 0
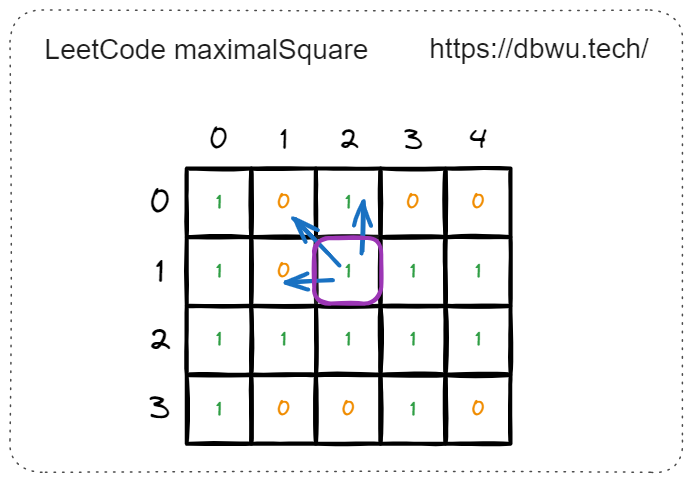
所以坐标 [1, 2] 可以构成的最大正方形边长等于:
$$ \begin{align*} min(0, 0, 0) + 1 = 1 \end{align*} $$
再比如,当计算坐标 [2, 3] 时,只要需要计算出其 上侧,左侧、左上角 的正方形边长:
- 上侧: [1, 3], 可以构成的最大正方形边长 = 1
- 左侧: [2, 2], 可以构成的最大正方形边长 = 1
- 左上角: [1, 2], 可以构成的最大正方形边长 = 1
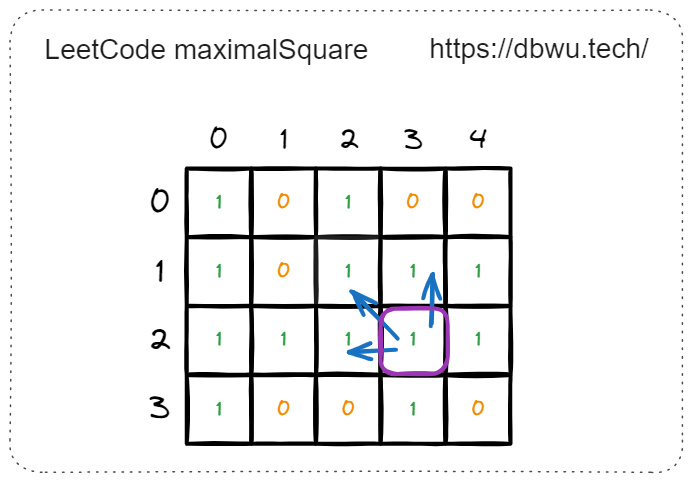
所以坐标 [2, 3] 可以构成的最大正方形边长等于:
$$ \begin{align*} min(1, 1, 1) + 1 = 2 \end{align*} $$
根据这两个示例和边界条件,可以推导出如下的状态转移方程:
$$ \begin{align*} F(i, j) = \begin{cases} \min( F(i-1, j), F(i, j-1), F(i-1, j-1) \ ) + 1 & \text {, } \text{matrix}[i][j] = 1 \\ 0 & \text{, } \text{matrix}[i][j] = 0 \end{cases} \end{align*} $$
当前坐标可以构成的最大正方形边长 等于其 上侧,左侧、左上角 的正方形边长中的最小值加一。
算法步骤
根据上面的分析过程和状态转移过程,可以得到如下的算法步骤:
- 定义问题状态:以矩阵中的每个元素作为 “新的正方形” 的右下角坐标,计算可以构成的 “最大正方形” 边长
- 状态转移方程:
F(i, j) = min{ F(i−1,j), F(i,j−1), F(i−1,j−1) } + 1 - 初始化:建立状态转移表 (一个二维数组),数组中所有元素初始化为 0, 表示以当前元素为坐标可以构成的最大正方形边长为 0
- 计算子问题:计算当前坐标的
上侧,左侧、左上角的 “最大正方形” 边长,并保存结果 - 计算原问题:从矩阵左上角开始一直遍历到右下角,逐个计算当前元素的 “最大正方形” 边长,同时更新目前已知的 “最大正方形” 边长 (变量 maxSide)
实现代码
计算出状态转移方程之后,剩下的事情就是将算法步骤直接翻译为代码就可以了,下面的是动态规划的实现代码。
// 动态规划
func maximalSquare(matrix [][]byte) int {
m := len(matrix)
if m == 0 {
return 0
}
n := len(matrix[0])
// dp[i][j]: 以 i 行 j 列为右下角所能构成的最大正方形边长
// dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
dp := make([][]int, m+1)
dp[0] = make([]int, n+1)
maxSide := 0
for i := 1; i <= m; i++ {
dp[i] = make([]int, n+1)
for j := 1; j <= n; j++ {
if matrix[i-1][j-1] == '1' {
dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
maxSide = max(maxSide, dp[i][j])
}
}
}
return maxSide * maxSide
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(x, y, z int) int {
if x < y && x < z {
return x
}
if y < z {
return y
}
return z
}
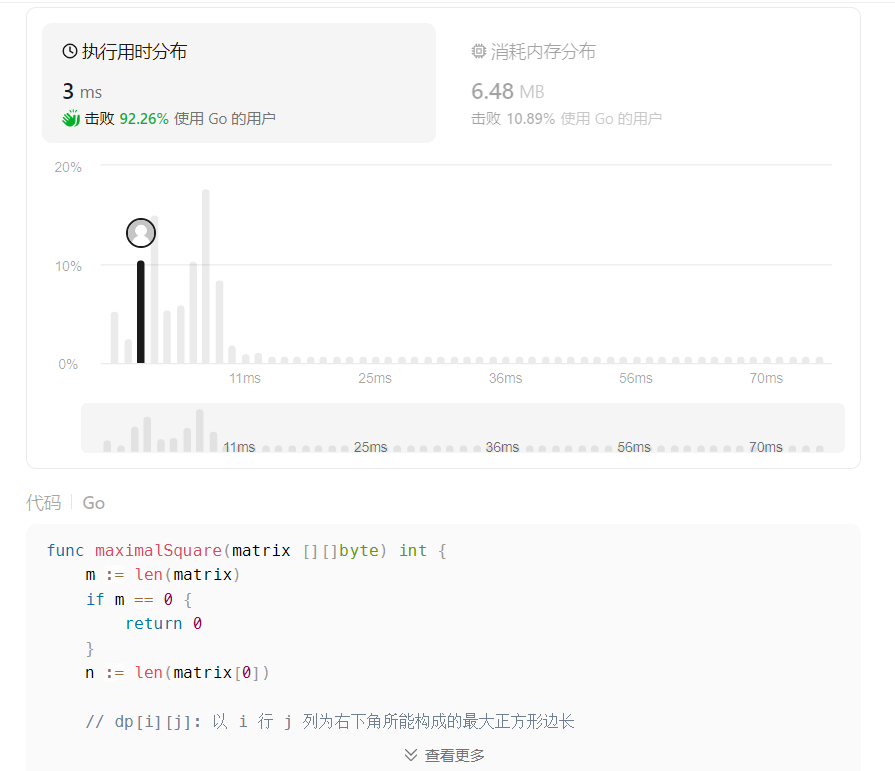
下面是动态规划代码的执行过程部分示例。