LeetCode 回溯 刷题模板
📖 概述
回溯 (Backtracking) 算法是一类用于寻找某些计算问题(尤其是约束满足问题)的解决方案,通过逐步构建解决方案的候选方案 (路径),并在确定候选方案无法完成某个目标时立即放弃该候选方案(“回溯”)。
回溯算法通常采用递归方式实现,在尝试每一种可能的问题解时,都会进入下一层递归,直到知道问题解或者确定当前路径无解,然后回溯到上一层,尝试更多可能的解。
回溯算法的本质是暴力穷举,假设问题的规模为 n, 解空间的大小为 m,回溯算法的时间复杂度通常可以表示为 O(m^n)。虽然某些场景下可以通过剪枝来进行优化,减少搜索空间,降低时间复杂度,但是 “最坏” 情况下回溯算法往往是指数级别的。
通过回溯算法解决数独问题的过程示例。
![]()
难点
回溯算法通常采用递归方式实现,在每一个递归过程中都要考虑多个选择,并不断进行递归调用,整个算法的控制流程会变得庞大复杂。此外,回溯算法涉及到对状态空间的搜索和维护,不同类型的问题有不同的解题思路和技巧,并没有像链表、二叉树等数据结构有固定的算法,因此解决回溯类算法时需要对问题本身进行抽象。
两个重要部分:
- 递归函数: 尝试每一种可能的解,递归搜索解空间
- 状态管理: 递归过程中,需要对状态进行管理,包括判断当前路径是否有效、选择新的当前路径、剪枝、回溯等操作
初学者面对回溯算法时,往往觉得难以理解和无从下手,主要原因在于: 对递归思想的理解和运用,以及对回溯过程中的状态空间搜索和剪枝策略的定义。
算法步骤
- 检测: 判断当前路径是否已经符合条件,如果已经符合条件,将当前路径添加到结果集中 (查找结果是什么,终止条件就是什么),终止当前递归,回溯到上一步
- 选择: 选择一个元素,形成新的当前路径 (候选方案),尝试将问题分解为子问题
- 剪枝: 根据问题的限制条件,判断当前路径是否有效,如果当前路径无效,终止当前递归,回溯到上一步
- 递归: 进入下一层递归,传入参数为当前路径和其他变量,继续解决子问题
- 回溯: 如果当前路径无解,回溯到上一步,撤销当前的选择,尝试更多其他解
对应的伪代码如下:
func Solution(问题参数) {
初始化结果集 result
初始化当前路径 path
backtrack(问题参数, path, result)
返回结果集 result
}
func backtrack(问题参数, path, result) {
if 判断当前路径是否已经符合条件 {
将当前路径加入结果集 result
return
}
for each 可选选择 in 候选集 {
选择: 将当前选择加入路径 path, 形成新的当前路径
剪枝: 结束当前递归,回溯到上一步
if 当前路径无效 {
return
}
递归: 进入下一层递归
backtrack(更新后的问题参数, path, result)
回溯: 撤销选择,将当前选择从路径 path 中移除
}
}
LeetCode 刷题模板
笔者根据 LeetCode 中的回溯相关算法题,整理了一个通用刷题模板。
func Solution(list []T) [][]T {
// 初始化结果集
var result [][]T
// 初始化当前路径
var path []T
// 回溯
backtrack(list, &path, &result)
// 返回结果集
return result
}
func backtrack(list []T, path *[]T, result *[][]T) {
// 判断当前路径是否满足条件
if 满足结束条件 {
// 将当前路径加入结果集
*result = append(*result, append([]T{}, path...))
return
}
// 遍历所有可能的选择
for _, 可选选择 := range 候选集 {
// 做出选择,形成新的当前路径
path = append(path, 可选选择)
// 继续向下搜索
backtrack(list, path, result)
// 撤销选择
path = path[:len(path)-1]
}
}
💡 典型题目 (图)
1. 电话号码的字母组合
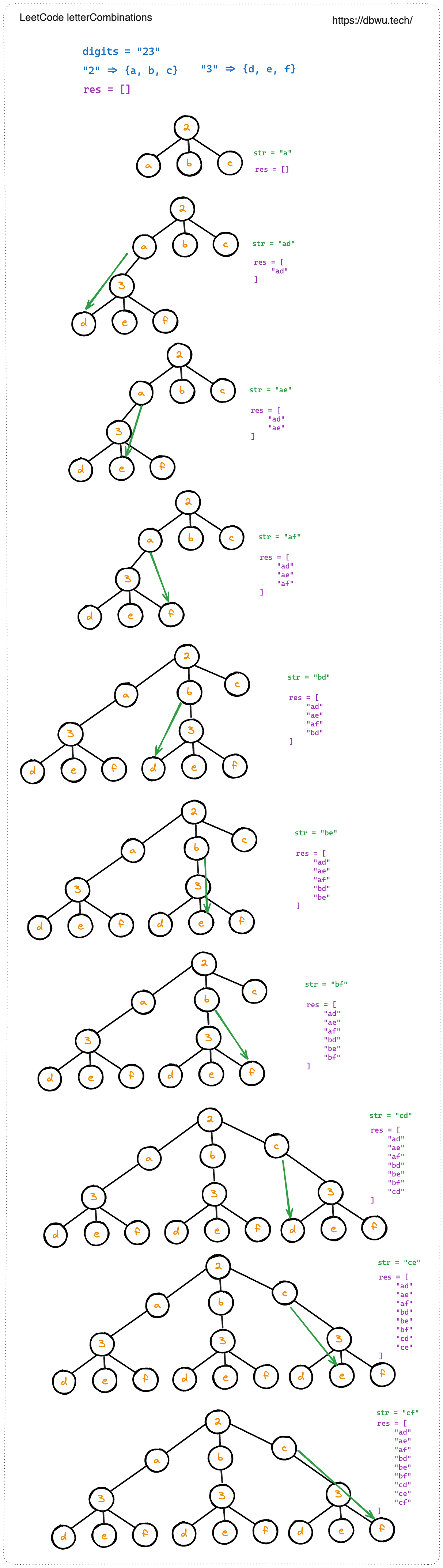
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

# 示例来自: https://leetcode.cn/
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
解题思路:
- 将电话键的数字和对应的字母形成一个映射 Map, 便于查找和组合
- 检测: 判断当前路径是否已经符合条件,也就是判断 当前路径的长度是否等于数字串的长度
- 选择: 遍历当前数字对应的字母列表,将当前字符添加到 当前路径 中,形成新的当前路径
- 剪枝: 因为题目要求找到所有的字母组合,所以不存在剪枝策略
- 递归: 将当前路径的长度加一,进入下一层递归
- 回溯: 选择当前字母列表的下一个字符,回溯到上一步,尝试更多其他组合
// 题解代码
var letterArray = []string{
"abc", //2
"def", //3
"ghi", //4
"jkl", //5
"mno", //6
"pqrs", //7
"tuv", //8
"wxyz", //9
}
func letterCombinations(digits string) []string {
if len(digits) == 0 {
return []string{}
}
var res []string
var str string
backtrack(digits, &res, str, 0)
return res
}
func backtrack(digits string, res *[]string, str string, begin int) {
// 如果当前路径的长度是否等于数字串的长度
// 正好满足一个组合,将当前路径加入到结果集中
if begin == len(digits) {
*res = append(*res, str)
} else {
// 获取当前数字对应的字符列表
// 如数字 2 对应的 {a, b, c}
strMap := letterArray[digits[begin]-'2']
for i := range strMap {
// 将当前字符添加到 当前路径 中,形成新的当前路径
// 将当前路径的长度 + 1
// 进入下一层递归
backtrack(digits, res, str+string(strMap[i]), begin+1)
}
}
}
2. 全排列
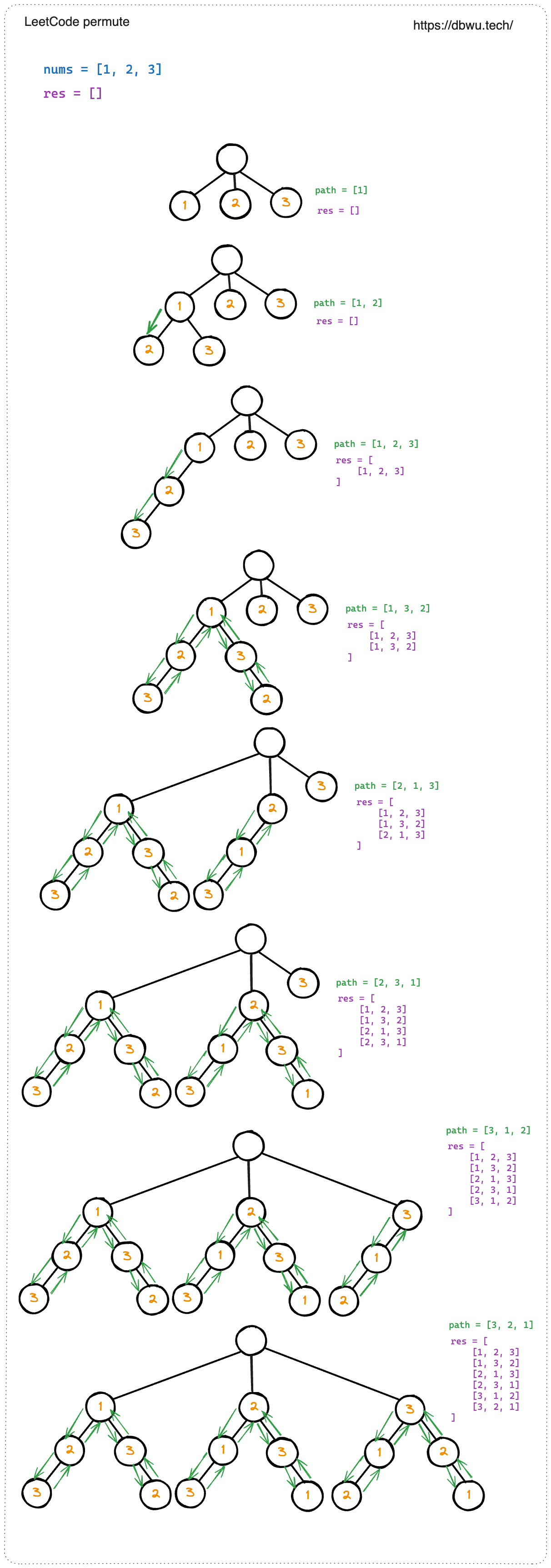
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
解题思路:
- 检测: 判断当前路径是否已经符合条件,也就是判断 当前路径的长度是否等于参数数组的长度
- 选择: 遍历数组,将当前元素添加到 当前路径 中,形成新的当前路径,同时将当前元素标记为已访问 (当前元素已经存在于 当前路径 中)
- 剪枝: 如果当前元素已访问,直接跳过
- 递归: 进入下一层递归
- 回溯: 将当前元素标记为未访问,同时从当前路径中删除当前元素,回溯到上一步,回溯尝试更多其他组合
// 题解代码
func permute(nums []int) [][]int {
var res [][]int
var path []int
// 初始化一个数组作为 Map
// 用来标记递归过程中已经存在于 “当前路径” 中的元素索引
// 避免单个元素被重复使用多次
// 例如正常情况下,[1, 2, 3] [1, 3, 2] 都会正常组合
// 但是 [1, 1, 1], [2, 2, 2] 属于元素重复使用,不能算作组合
var visited = make([]bool, len(nums))
backtrack(nums, &path, &visited, &res)
return res
}
func backtrack(nums []int, path *[]int, visited *[]bool, res *[][]int) {
// 当前路径的长度是否等于参数数组的长度
// 正好满足一个组合,将当前路径加入到结果集中
if len(*path) == len(nums) {
// 注意这里要拷贝当前路径中的元素
// 因为当前路径变量 path 会在递归过程中发生变化
row := make([]int, len(nums))
copy(row, *path)
// 将拷贝后的路径添加到结果集中
*res = append(*res, row)
return
}
// 遍历数组,执行递归 + 回溯操作
for i, v := range nums {
// 剪枝策略
// 如果当前元素未访问
if !(*visited)[i] {
// 将当前元素添加到 当前路径 中,形成新的当前路径
(*visited)[i] = true
// 将当前元素标记为已访问
*path = append(*path, v)
// 进入下一层递归
backtrack(nums, path, visited, res)
// 将当前元素标记为未访问
(*visited)[i] = false
// 从当前路径中删除当前元素
// 回溯到上一步,尝试更多可能的解
*path = (*path)[:len(*path)-1]
}
}
}
3. 组合总和
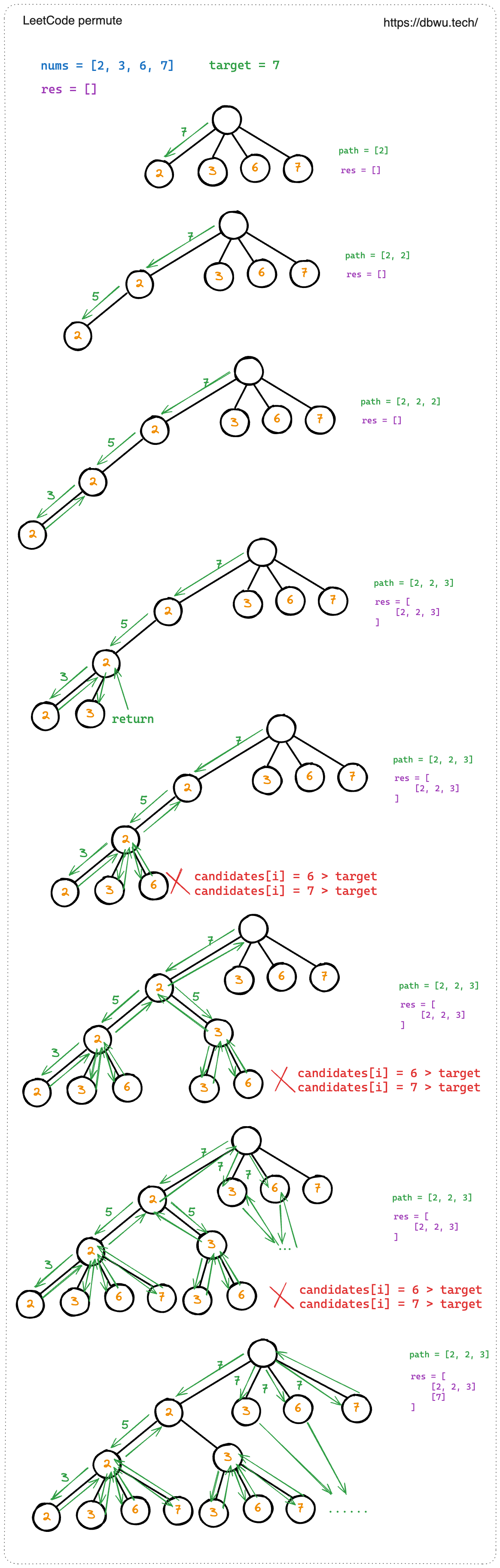
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
# 示例来自: https://leetcode.cn/
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
解题思路:
- 检测: 判断当前路径是否已经符合条件,也就是判断 当前查找目标值等于 0
- 选择: 从指定的起始位置开始遍历数组,将当前元素添加到 当前路径 中,形成新的当前路径
- 剪枝: 如果当前元素大于目标值,直接跳过
- 递归: 将查找目标值减去当前元素,进入下一层递归
- 回溯: 当前路径中删除当前元素,回溯到上一步,回溯尝试更多其他组合
// 题解代码
func combinationSum(candidates []int, target int) [][]int {
if len(candidates) == 0 {
return nil
}
var path []int
var res [][]int
// 为了在递归过程中优化剪枝
// 提前对数组进行排序
sort.Ints(candidates)
backtrack(candidates, target, 0, &path, &res)
return res
}
func backtrack(candidates []int, target, begin int, path *[]int, res *[][]int) {
// 如果当前查找目标值等于 0
// 正好满足一个组合,将当前路径加入到结果集中
if target == 0 {
// 这里使用了另外一种语法来实现追加功能
*res = append(*res, append([]int{}, *path...))
return
}
for i := begin; i < len(candidates); i++ {
// 剪枝 (前提:已排序)
// 数组排序之后
// 如果当前元素大于目标值,那么当前元素之后的所有元素都不可能出现有效的组合了
// 例如数组排序之后为 [2,3,6,7], target = 5
// 那么当前元素遍历到 6 时,就可以直接剪枝了
if candidates[i] > target {
return
}
// 将当前元素添加到 当前路径 中,形成新的当前路径
*path = append(*path, candidates[i])
// candidates 中的 同一个 数字可以 无限制重复被选取
// i 作为起点,查找 target-candidates[i]
// 指定起始位置为当前位置
backtrack(candidates, target-candidates[i], i, path, res)
// 从当前路径中删除当前元素
// 回溯到上一步,尝试更多可能的解
*path = (*path)[:len(*path)-1]
}
}