LeetCode BFS 刷题模板
📖 概述
BFS (广度优先搜索) 是一种在树或图数据结构中搜索满足给定条件的节点的算法,其基本思想是从起始节点 (通常是根节点) 出发,探索当前深度的所有节点,然后再移动到下一个深度级别的节点,搜索过程中,需要额外的内存(通常是队列)来存储已经遍历到但尚未继续搜索的子节点,队列长度就是未搜索子节点的个数,直到搜索完所有节点或者找到满足条件的节点 (或路径),算法结束。
DFS: 不撞南墙不回头
BFS: 步步为营
算法基本步骤
- 初始化队列
- 将起始节点 (通常是根节点) 加入到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个节点
- 对该节点进行逻辑处理 (例如标记已访问、计算数据、更新当前层级等)
- 将该节点相邻的所有 (或者未访问) 节点全部加入到队列中
- 重复第 3 步,直到队列为空或者所有节点均被访问
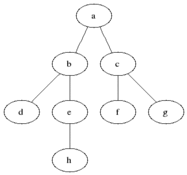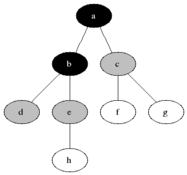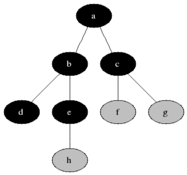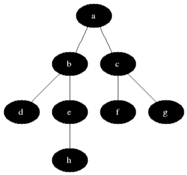
执行过程示例
下面是一个典型的图 (同时也是一棵树) 数据结构:
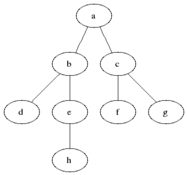
对该图执行 BFS 算法时,具体的执行过程中,每个节点被访问的顺序如图所示:
伪代码
BFS 算法通常用于解决以下问题:
- 求解最短路径问题 (路径上没有权重,也就是未加权图),如迷宫最短路径、网络节点间的最短通路
- 在树或图数据结构中进行层级遍历或层级搜索
- 判断图中是否存在环路或特定路径
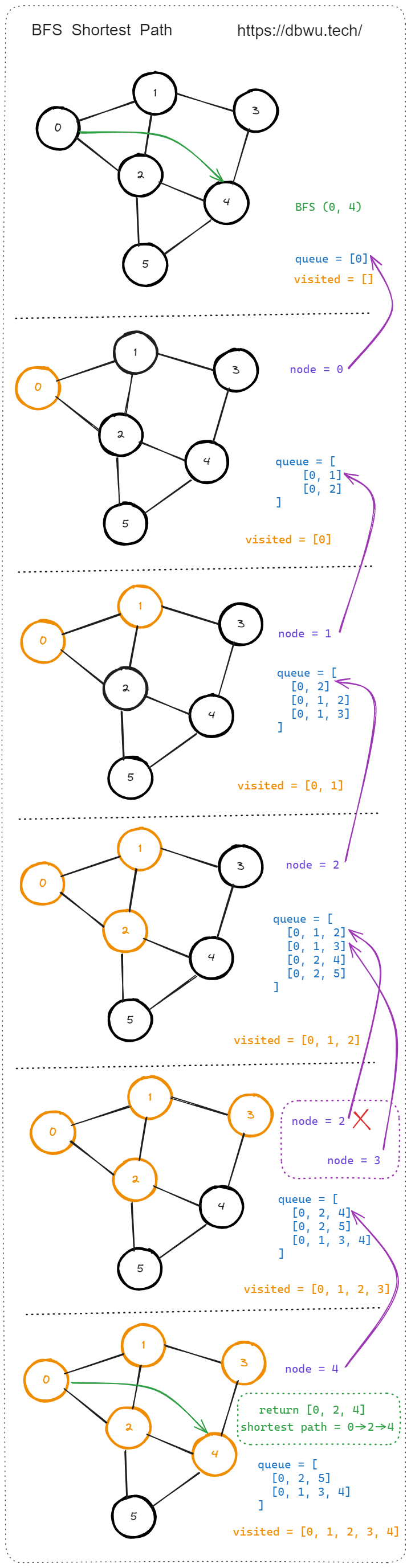
下面的 求解最短路径问题 对应的 Golang 伪代码:
// 使用邻接表 表示图的数据结构
type Graph struct {
Nodes map[int][]int
}
// 广度优先搜索
// 找到从起始节点到目标节点的最短路径
func (g *Graph) BFS(start, target int) []int {
// 初始化队列,用于存储路径
// 将起始节点加入到队列中
queue := [][]int{{start}}
// 记录节点是否已访问过
visited := make(map[int]bool)
// 循环遍历队列
for len(queue) > 0 {
// 从队列中取出第一个路径
path := queue[0]
// 将取出的路径从队列中移除
queue = queue[1:]
// 取出当前路径的最后一个节点
node := path[len(path)-1]
// 将当前节点标记为已访问
visited[node] = true
// 如果当前节点是目标节点,直接返回当前路径即可
if node == target {
return path
}
// 遍历当前节点的所有邻居节点
for _, neighbor := range g.Nodes[node] {
if !visited[neighbor] {
// 如果邻居节点未访问过,则将其加入路径形成新的路径
newPath := make([]int, len(path))
copy(newPath, path)
newPath = append(newPath, neighbor)
// 将新的路径加入队列
queue = append(queue, newPath)
}
}
}
// 未找到路径返回空
return nil
}
// 计算起始节点 0 到目标节点 10 的最短路径
graph.BFS(0, 10)
💡 BFS 和图
LeetCode 中的 BFS (图数据结构) 相关题目都是在 BFS 基础上加上题目的具体逻辑即可,解题步骤 (模板) 和 BFS 算法一样可以分为四步:
- 初始化队列,节点访问标记等数据结构
- 将起始节点添加到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个节点
- 处理当前节点:对当前节点进行任何必要的操作,例如更新距离、记录路径等
- 遍历当前节点的邻居节点:对当前节点的邻居节点进行遍历,检查它们是否已经被访问过
- 如果邻居节点尚未被访问过,则将其加入队列,并标记为已访问
- 重复第 3 步,直到队列为空或者所有节点均被访问
// BFS 刷题模板代码 (针对图数据结构)
func bfs(node *Node) *Node {
// 边界处理
if node == nil {
return nil
}
// 声明节点访问标记 Map
visited := make(map[*Node]bool)
// 将起始节点添加到队列中
queue := []*Node{node}
// 将起始节点标记为已访问
visited[node] = true
for len(queue) > 0 {
// 从队列中取出第一个节点
top := queue[0]
// 第一个节点出队
queue = queue[1:]
// 处理具体的逻辑
...
// 遍历当前节点的邻居节点
for _, neighbor := range top.Neighbors {
if !visited[neighbor] {
// 如果邻居节点尚未被访问过,则将其加入队列,并标记为已访问
queue = append(queue, neighbor)
visited[neighbor] = true
}
}
}
return ...
}
💡 典型题目 (图)
为了更好地比较 DFS 算法和 BFS 算法的差异,本文会使用 这篇 DFS 刷题模板文章中 相同的图算法题目作为示例题解。
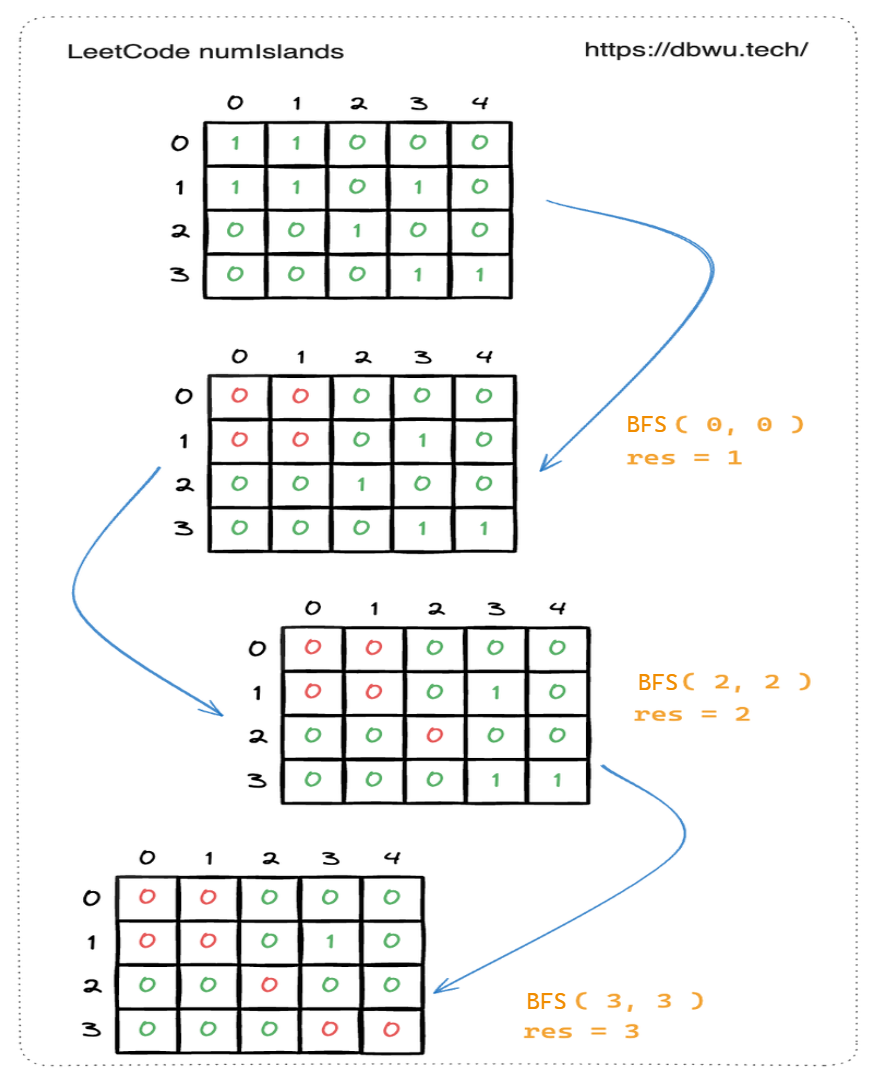
1. 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
# 示例来自: https://leetcode.cn/
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
快速套模板:
- 遍历二维网格
- 如果当前坐标为 “陆地”,岛屿数量 + 1,同时执行 BFS 算法继续探索
- 在单次 BFS 算法过程中,循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个坐标,如果该坐标为 “陆地”,将该坐标从 “陆地” 标记为从 “水”,避免重复计算
- 以该坐标为中心,将上下左右四个方向的坐标分别加入队列
- 重复第 1, 2 步,直到队列为空
- 二维网格遍历结束,所有坐标都被标记为 “水”
// 题解代码
func numIslands(grid [][]byte) int {
res := 0
for i := 0; i < len(grid); i++ {
for j := 0; j < len(grid[0]); j++ {
if grid[i][j] == '1' {
// 如果找到一块陆地,以该坐标为中心,上下左右四个方向继续探索
res++
bfs(grid, i, j)
}
}
}
return res
}
func bfs(grid [][]byte, i, j int) {
// 将当前的起始坐标加到队列
// 这里的队列使用二维数组表示
queue := [][2]int{}
queue = append(queue, [2]int{i, j})
for len(queue) > 0 {
// 从队列中取出第一个坐标
i, j := queue[0][0], queue[0][1]
// 第一个坐标出队
queue = queue[1:]
// 如果坐标未越界 并且 当前坐标是陆地
if i >= 0 && i < len(grid) && j >= 0 && j < len(grid[0]) && grid[i][j] == '1' {
// 已经探索过的坐标标记为 0, 避免重复计算
grid[i][j] = '0'
// ⬆ 方向继续探索
queue = append(queue, [2]int{i - 1, j})
// ⬇ 方向继续探索
queue = append(queue, [2]int{i + 1, j})
// <- 方向继续探索
queue = append(queue, [2]int{i, j - 1})
// -> 方向继续探索
queue = append(queue, [2]int{i, j + 1})
}
}
}
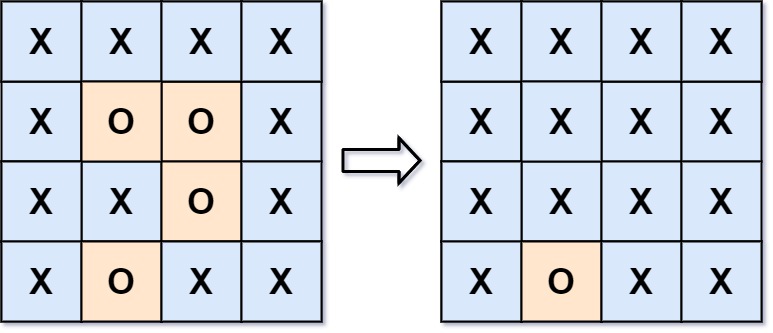
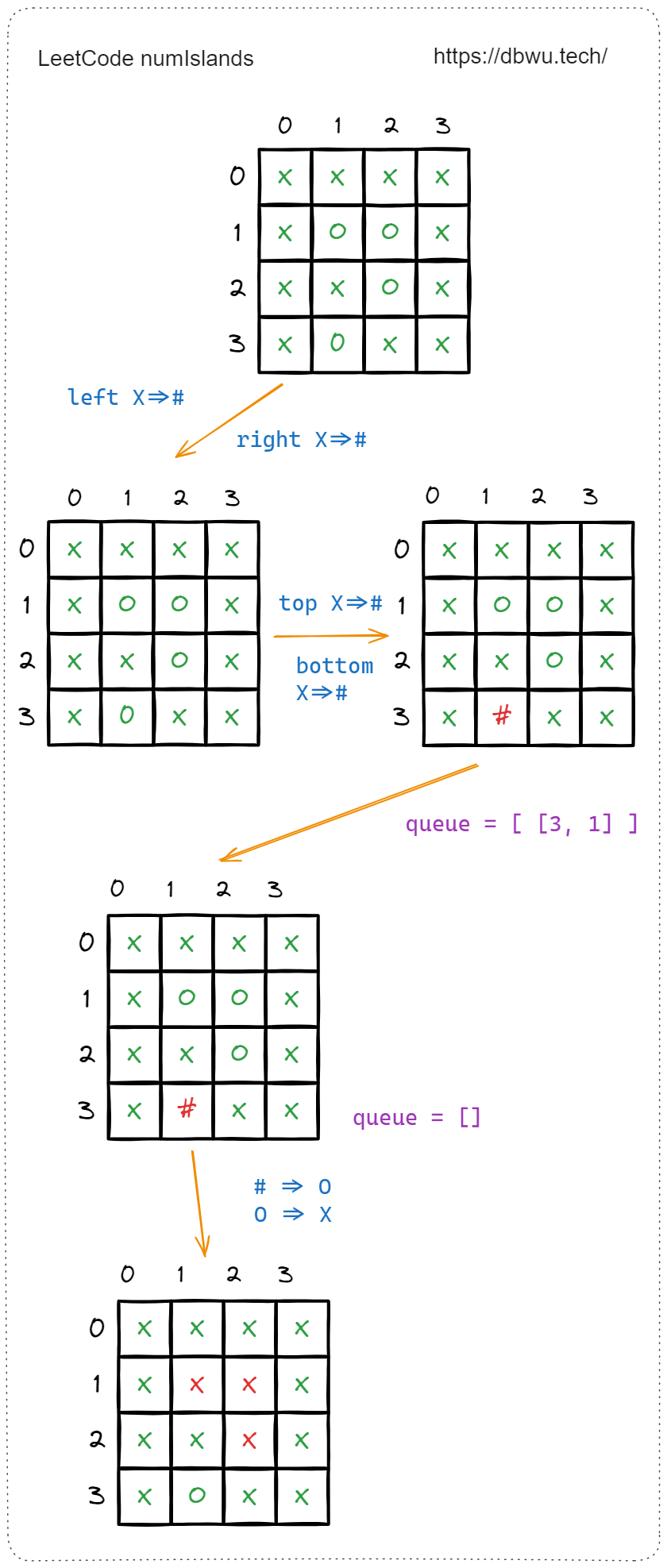
2. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
解题思路:
题目解释中提到:任何边界上的 O 都不会被填充为 X, 所有的不被包围的 O 都直接或间接与边界上的 O 相连。那么只需要将所有可以连通的进行标记,剩下的就是无法连通的。
题目要求四个边界上面的格子 ‘O’ 不需要被更新,那么如何在 DFS 的递归执行过程中规避掉这个问题呢?我们可以使用一个额外的字符 # 作为临时字符来替换掉边界上的 ‘O’, 专门用于标记已经更新过的格子,最后再将临时字符 # 的格子替换为 ‘O’。
快速套模板:
- 初始化队列
- 对左右边界和上下边界进行预处理,将 ‘O’ 的坐标标记为 ‘#’ 并加入队列
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个节点
- 以该坐标为中心,上下左右四个方向继续探索
- 重复第 3 步,直到队列为空或者所有节点均被访问
- 所有值为 ‘O’ 的坐标,就是无法从上下左右边界到达的坐标,直接标记为 ‘X’, 将所有值为 ‘#’ 的坐标,标记为 ‘O’
// 题解代码
func bfs(board [][]byte) {
// 边界处理
if len(board) == 0 || len(board[0]) == 0 {
return
}
rows, cols := len(board), len(board[0])
var queue [][2]int
// 将左右边界进行标记为 "已连通"
for row := 0; row < rows; row++ {
if board[row][0] == 'O' {
// 将值为 'O' 的坐标加入队列
queue = append(queue, [2]int{row, 0})
board[row][0] = '#'
}
if board[row][cols-1] == 'O' {
// 将值为 'O' 的坐标加入队列
queue = append(queue, [2]int{row, cols - 1})
board[row][cols-1] = '#'
}
}
// 将上下边界进行标记为 "已连通"
for col := 1; col < cols-1; col++ {
if board[0][col] == 'O' {
// 将值为 'O' 的坐标加入队列
queue = append(queue, [2]int{0, col})
board[0][col] = '#'
}
if board[rows-1][col] == 'O' {
// 将值为 'O' 的坐标加入队列
queue = append(queue, [2]int{rows - 1, col})
board[rows-1][col] = '#'
}
}
dx := []int{0, 0, -1, 1} // x: 上下左右
dy := []int{-1, 1, 0, 0} // y: 上下左右
for len(queue) > 0 {
// 从队列中取出第一个坐标
top := queue[0]
// 第一个坐标出队
queue = queue[1:]
// 以该坐标为中心,上下左右四个方向继续探索
for i := 0; i < 4; i++ {
x, y := top[0]+dx[i], top[1]+dy[i]
if x > 0 && x < rows && y > 0 && y < cols && board[x][y] == 'O' {
queue = append(queue, [2]int{x, y})
board[x][y] = '#'
}
}
}
// 现在从矩阵的最外侧作为出发点
// 上下左右四个方向已经连通
// 只需要遍历一次矩阵
// 将 # 修改为 0, 因为这些属于边界上的 0
// 将 0 改为为 X, 因为这些不属于边界上的 0
for row := 0; row < rows; row++ {
for col := 0; col < cols; col++ {
if board[row][col] == '#' {
board[row][col] = 'O'
} else if board[row][col] == 'O' {
board[row][col] = 'X'
}
}
}
}
3. 克隆图
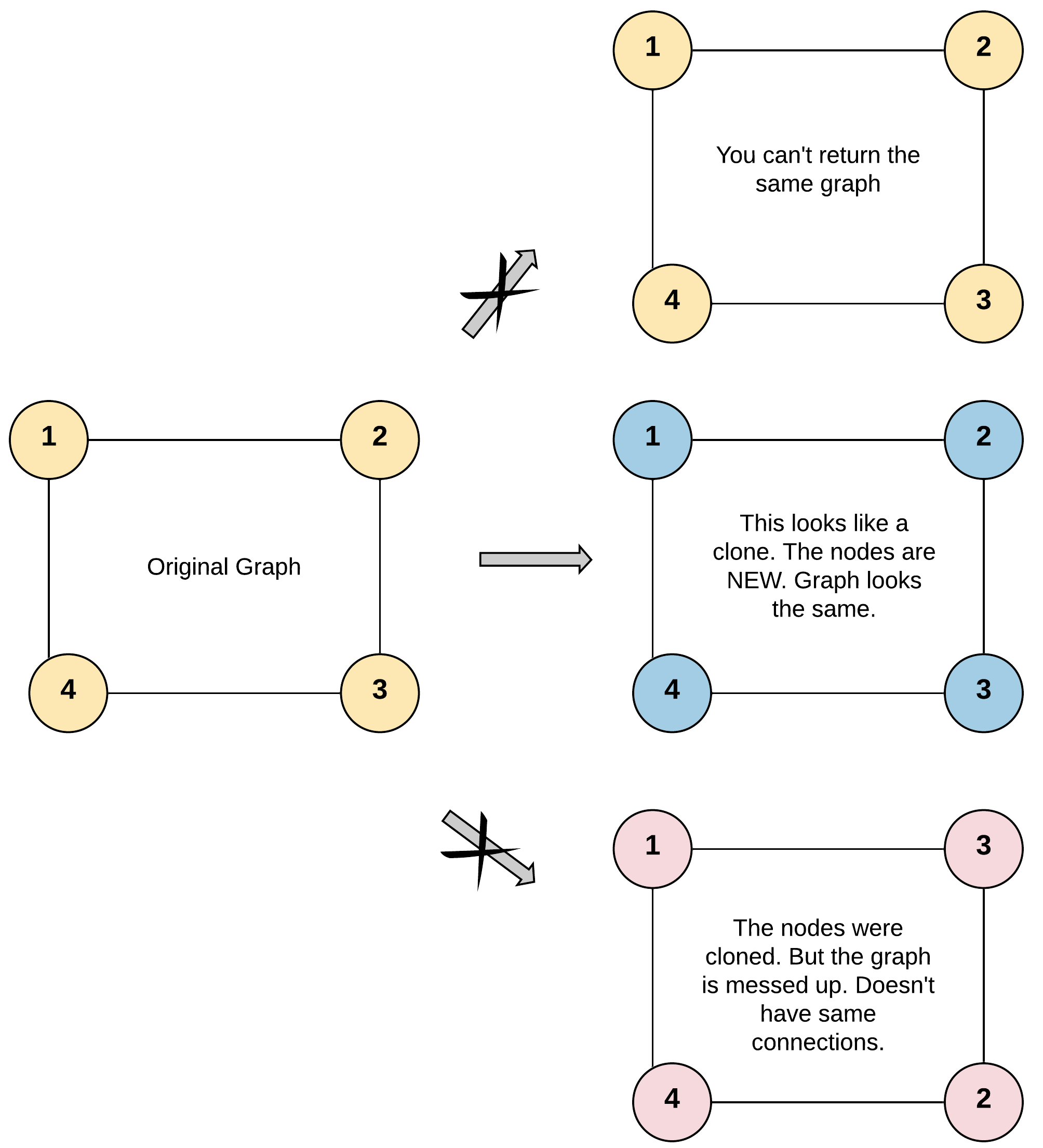
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
节点的深度拷贝需要满足两个条件:
- 新节点必须和源节点的值一样,并且拥有新的内存地址空间和数据结构
- 各个新节点之间的关系必须和源节点之间的关系一致
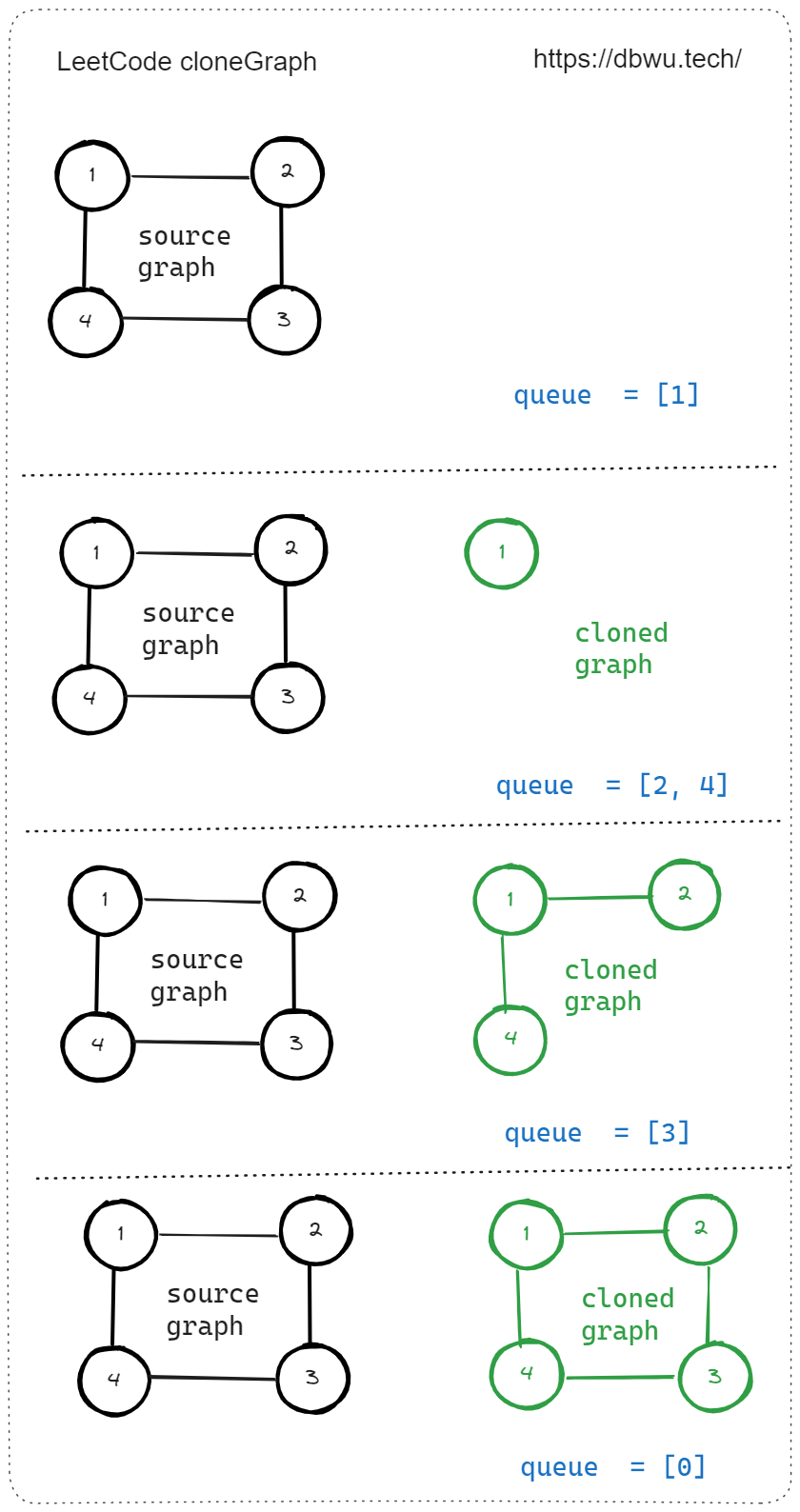
快速套模板:
- 初始化队列,克隆节点 Map
- 将起始节点添加到队列中,同时克隆当前节点并添加源节点到克隆节点的映射
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个节点
- 遍历当前节点的邻居节点,如果邻居节点还未被克隆过,克隆邻居节点并添加源节点到克隆节点的映射,最后将邻居节点加入队列
- 重复第 3 步,直到队列为空或者所有节点均被访问
// 题解代码
func cloneGraph(node *Node) *Node {
return bfs(node, make(map[*Node]*Node))
}
func bfs(node *Node) *Node {
// 边界处理
if node == nil {
return node
}
// 声明节点访问标记 Map
// 除了访问标记外,该 Map 还有另外一个作用
// 那就是将源节点和克隆节点进行映射
visited := make(map[*Node]*Node)
// 克隆起始节点 (将起始节点标记为已访问)
visited[node] = &Node{node.Val, []*Node{}}
// 将起始节点添加到队列中
queue := []*Node{node}
for len(queue) > 0 {
// 从队列中取出第一个节点
top := queue[0]
// 第一个节点出队
queue = queue[1:]
for _, v := range top.Neighbors {
if _, ok := visited[v]; !ok {
// 如果邻居节点还未被克隆过 (未被访问过)
// 克隆邻居节点 (标记为已访问)
visited[v] = &Node{v.Val, []*Node{}}
// 将邻居节点添加到队列中
queue = append(queue, v)
}
// 更新当前节点的邻居节点
visited[top].Neighbors = append(visited[top].Neighbors, visited[v])
}
}
// 返回起始节点对应的克隆新节点
return visited[node]
}
💡 BFS 和二叉树
BFS 算法最经典应用场景之一,就是二叉树层级的层级遍历和搜索相关问题。
算法复杂度
时间复杂度:O(N),其中 N 是二叉树中的节点个数,搜索过程中 (最坏情况下) 需要对每个节点访问一次。
空间复杂度:O(W),其中 W 是二叉树的最大宽度,空间复杂度和树的高度正相关,对于高度为 H 的二叉树,空间复杂度最多为 O(W) = O((H-1)^2),也就是满二叉树的情况。
最坏情况下,二叉树的高度等于节点个数,也就是类似如下图所示 “链表” 的二叉树结构。
1
/
2
/
3
/
4
/
5
💡 解决二叉树的层级遍历相关问题时,BFS 算法和 DFS 算法的时间复杂度和空间复杂度是一样的,但是 BFS 算法相对直观和容易理解。
刷题模板
LeetCode 中的二叉树 BFS 相关题目都是在 BFS 算法基础上加上具体逻辑即可,因为只需要一个额外的队列数据结构,再加上二叉树的层级遍历过程非常直观,所以只需要在模板代码的基础上略微修改就可以快速刷题。
- 初始化队列
- 将根节点加入到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 从队列中取出第一个节点
- 对该节点进行逻辑处理
- 将该节点左右子节点加入到队列中
- 重复第 3 步,直到队列为空
下面是一个使用 BFS 层级遍历二叉树的代码模板。
func levelOrder(root *TreeNode) {
// 边界处理
if root == nil {
return nil
}
// 初始化队列
// 将根节点加入到队列中
queue := []*TreeNode{root}
for len(queue) > 0 {
// 记录当前层的节点数
// 便于内部循环处理当前所在层的所有节点
length := len(queue)
// 声明初始化用于处理当前层逻辑的数据结构
...
// 处理当前层的所有节点
for i := 0; i < length; i++ {
// 从队列中取出第一个节点
node := queue[0]
// 第一个节点出队
queue = queue[1:]
// 处理具体的逻辑
...
// 将当前节点的左右子节点加入队列
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
// 处理具体的逻辑
...
}
return result
}
💡 典型题目 (二叉树)
为了更好地比较 DFS 算法和 BFS 算法的差异,本文会使用 这篇 DFS 刷题模板文章中 相同的二叉树题目作为示例题解。
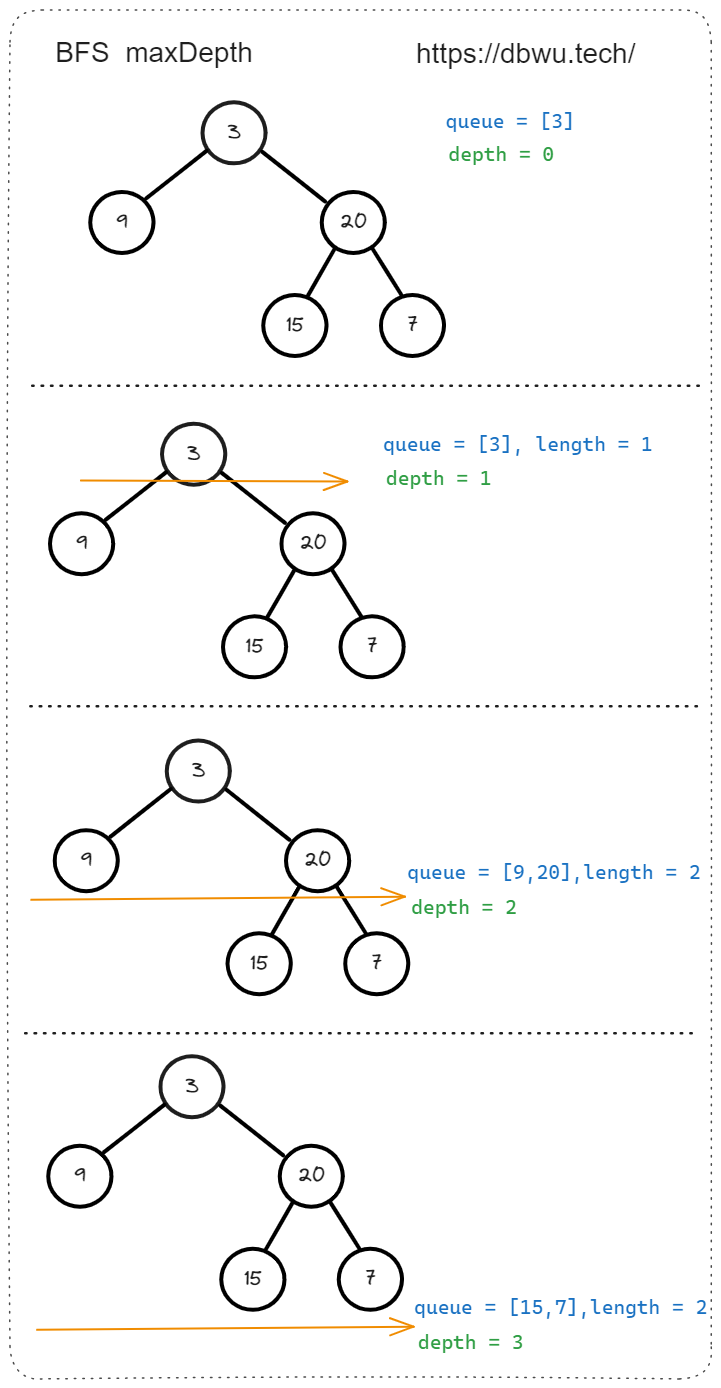
1. 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
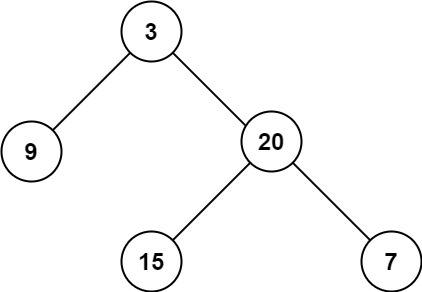
如图所示的 树 的深度为 3。
快速套模板:
- 初始化队列
- 将根节点加入到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 初始化 “当前层的总和” 为 0
- 挨个取出当前层的所有节点
- 将当前节点的值累加到 “当前层的总和”,同时将当前节点的左右子节点添加到队列中
- 计算当前层的所有节点的平均值并追加到结果集中
- 重复第 3 步,直到队列为空
// 题解代码
func maxDepth(root *TreeNode) int {
// 边界处理
if root == nil {
return 0
}
// 初始化队列
// 将根节点加入到队列中
queue := []*TreeNode{root}
// 记录已到达树的深度
depth := 0
for len(queue) > 0 {
// 更新已到达树的深度
depth++
// 记录当前层的节点数
length := len(queue)
for i := 0; i < length; i++ {
// 将当前节点的左右子节点加入队列
if queue[i].Left != nil {
queue = append(queue, queue[i].Left)
}
if queue[i].Right != nil {
queue = append(queue, queue[i].Right)
}
}
// 利用 Go 语言的语法糖处理队列的出队操作
queue = queue[length:]
}
return depth
}
2. 二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。
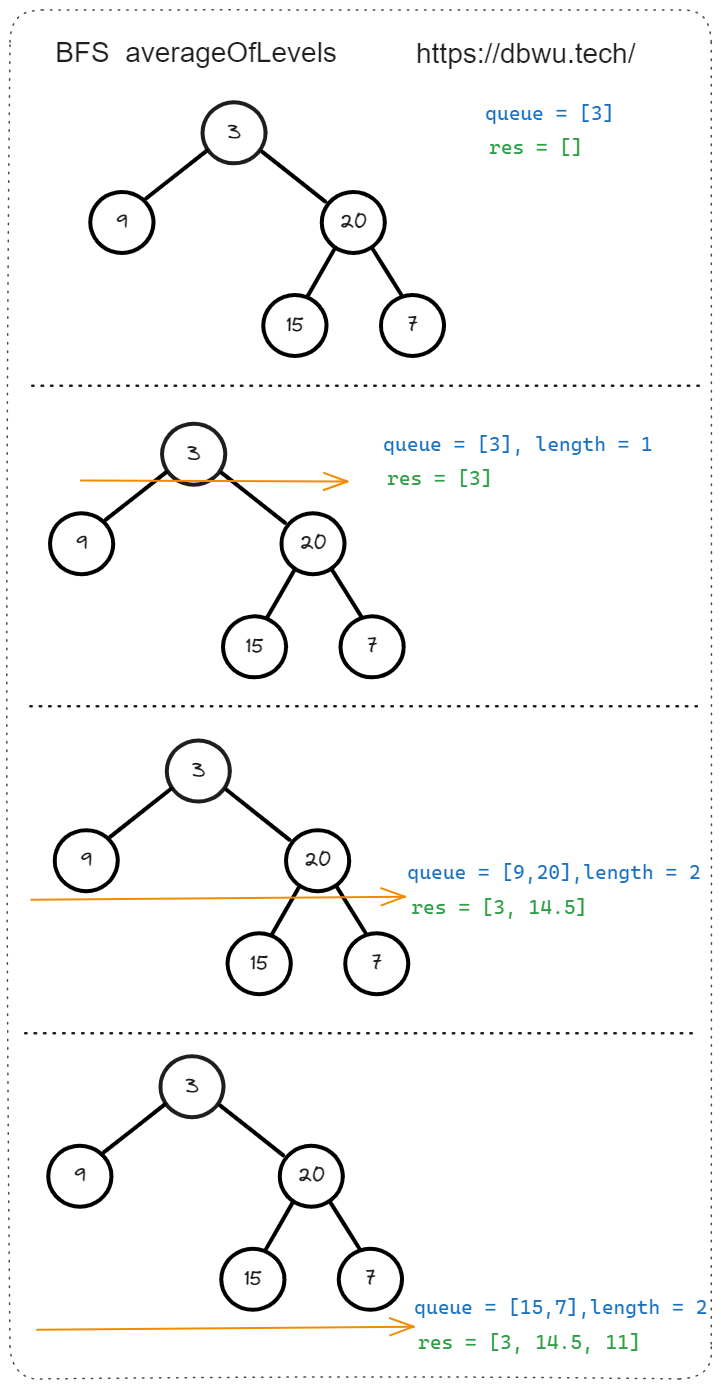
给出上图所示的二叉树,会输出如下答案:
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
快速套模板:
- 初始化队列
- 将根节点加入到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 初始化 “当前层的总和” 为 0
- 挨个取出当前层的所有节点
- 将当前节点的值累加到 “当前层的总和”,同时将当前节点的左右子节点添加到队列中
- 计算当前层的所有节点的平均值并追加到结果集中
- 重复第 3 步,直到队列为空
// 题解代码
func averageOfLevels(root *TreeNode) []float64 {
// 边界处理
var res []float64
if root == nil {
return res
}
// 初始化队列
// 将根节点加入到队列中
queue := []*TreeNode{root}
for len(queue) > 0 {
length := len(queue)
// 初始化 “当前层的总和” 为 0
sum := 0
for i := 0; i < length; i++ {
// 将当前节点的值累加到 “当前层的总和”
sum += queue[i].Val
// 将当前节点的左右子节点加入队列
if queue[i].Left != nil {
queue = append(queue, queue[i].Left)
}
if queue[i].Right != nil {
queue = append(queue, queue[i].Right)
}
}
// 利用 Go 语言的语法糖处理队列的出队操作
queue = queue[length:]
// 计算当前层的所有节点的平均值并追加到结果集中
res = append(res, float64(sum)/float64(length))
}
return res
}
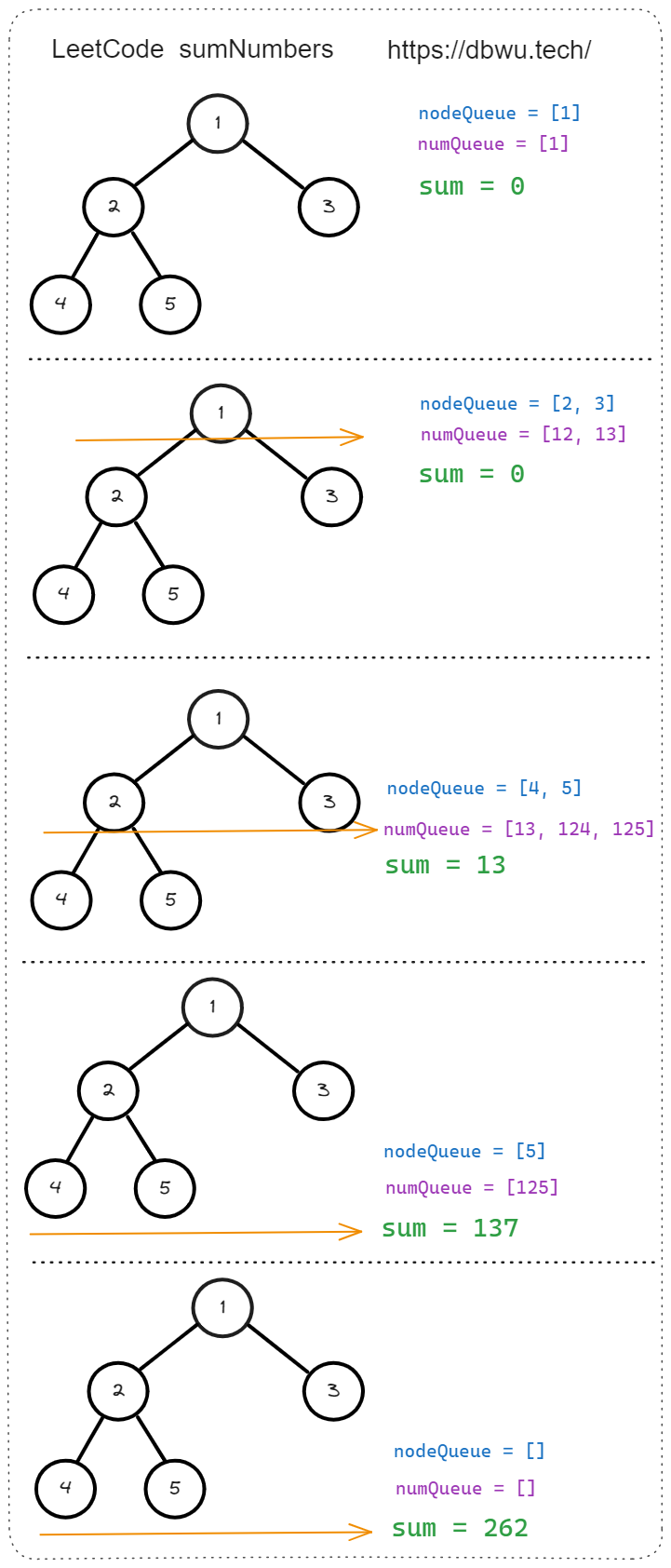
3. 二叉树根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。 叶节点 是指没有子节点的节点。
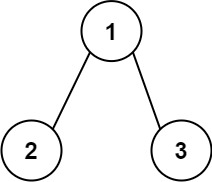
# 如图所示
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
解题思路:
和 DFS 算法不同的是: 使用 BFS 算法层级遍历二叉树时,只有遍历到了某个具体的叶子节点时,才能计算出这条路径上面的数字总和,所以在到达叶子节点之前,对于已经遍历过的层级节点路径,需要单独使用一个队列 (数组) 保存起来。
快速套模板:
- 初始化节点队列和 路径数字总和队列
- 将根节点加入到节点队列中,将根节点的值加入到 路径数字总和队列 中
- 循环遍历队列 (节点队列不为空的前提下),执行下列操作:
- 从节点队列中取出第一个节点
node,从 路径数字总和队列 中取出第一个数字num - 如果当前节点是叶子节点,就将
num加入到结果总和中 - 如果当前节点不是叶子节点,将
node的左右子节点加入节点队列,将num和node的左右子节点的值重新计算,然后加入 路径数字总和队列
- 从节点队列中取出第一个节点
- 重复第 3 步,直到节点队列为空
// 题解代码
func sumNumbers(root *TreeNode) int {
// 边界处理
if root == nil {
return 0
}
// 返回值, 路径总和
sum := 0
// 初始化两个队列
// 将根节点加入到节点队列中
nodeQueue := []*TreeNode{root}
// 将根节点的值加入到 路径数字总和队列 中
numQueue := []int{root.Val}
for len(nodeQueue) > 0 {
// 获取当前节点
node := nodeQueue[0]
nodeQueue = nodeQueue[1:]
// 获取当前 “路径和”
num := numQueue[0]
numQueue = numQueue[1:]
if node.Left == nil && node.Right == nil {
// 叶子节点,直接将当前的 “路径和” 累加到返回值总和中
sum += num
} else {
// 将当前节点的左右子节点加入队列
// 将 当前 “路径和” 和当前节点的左右子节点的值 重新计算
// 然后加入 路径数字总和队列
if node.Left != nil {
nodeQueue = append(nodeQueue, node.Left)
numQueue = append(numQueue, num*10+node.Left.Val)
}
if node.Right != nil {
nodeQueue = append(nodeQueue, node.Right)
numQueue = append(numQueue, num*10+node.Right.Val)
}
}
}
return sum
}
4. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
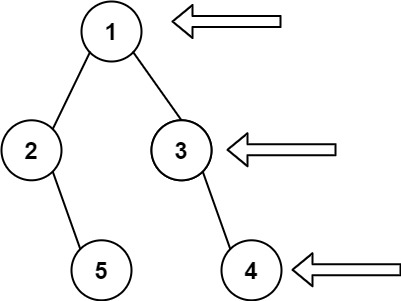
如图所示的树的右视图为 [1, 3, 4] 也就是树的每一层最右侧的节点值组成的列表。
快速套模板:
- 初始化队列
- 将根节点加入到队列中
- 循环遍历队列 (队列不为空的前提下),执行下列操作:
- 将当前层级中的最右边的节点值添加到返回结果数组中
- 重复第 3 步,直到队列为空
// 题解代码
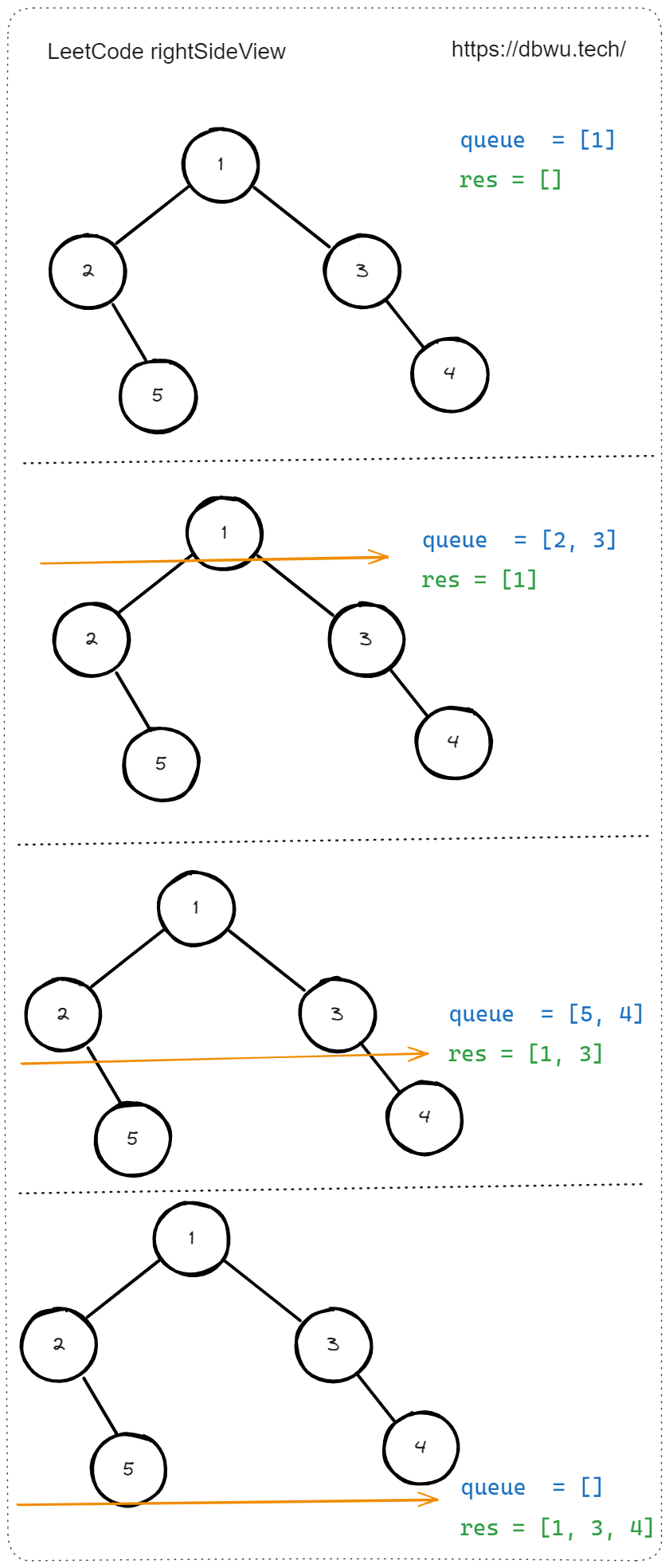
func rightSideView(root *TreeNode) []int {
// 边界处理
if root == nil {
return []int{}
}
// 声明返回值数组
var res []int
// 初始化两个队列
// 将根节点加入到节点队列中
queue := []*TreeNode{root}
for len(queue) > 0 {
length := len(queue)
for i := 0; i < length; i++ {
// 将当前节点的左右子节点加入队列
if queue[i].Left != nil {
queue = append(queue, queue[i].Left)
}
if queue[i].Right != nil {
queue = append(queue, queue[i].Right)
}
}
// 将当前队列 (层级) 中的最右边的节点值添加到返回结果数组中
res = append(res, queue[length-1].Val)
// 利用 Go 语言的语法糖处理队列的出队操作
queue = queue[length:]
}
return res
}
💡 其他送分题
熟练掌握使用 BFS 算法层级遍历二叉树之后,相关的题目全部是送分题。
1. 翻转二叉树
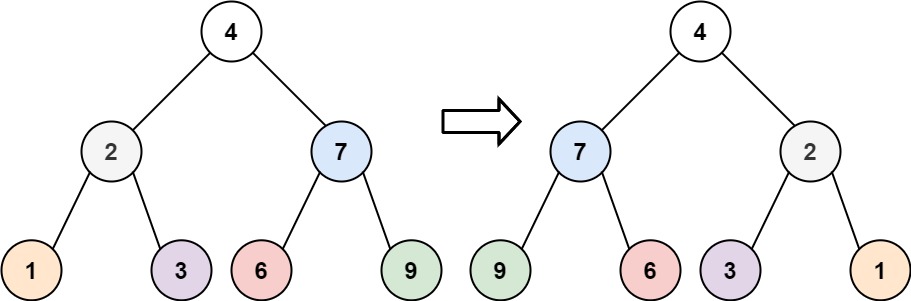
解题思路:
- BFS 层级遍历
- 每一层中 反转当前队列中的所有节点
2. 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
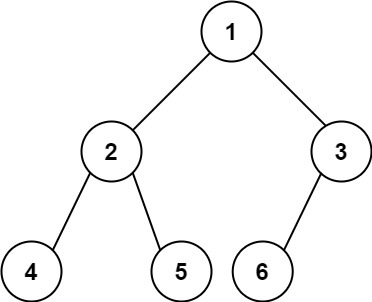
如图所示的二叉树节点数量为 6。
解题思路:
BFS 层级遍历时将当前队列中的所有节点数量进行累计,BFS 遍历结束后反复累计数量值。
3. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。(即逐层地,从左到右访问所有节点)。
这道题几乎就是 BFS 算法稍微一改就可以 AC 了。
解题思路:
- BFS 层级遍历,将当前层级中的所有节点值添加到一维数组中
- 将一维数组追加到返回值二维数组中
4. 二叉树的锯齿形层序遍历
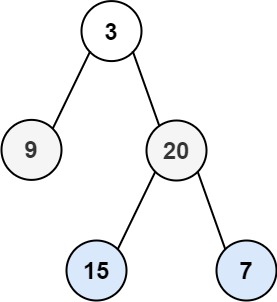
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。

如图所示的二叉树,使用锯齿层序遍历返回值为 [[3],[20,9],[15,7]]。
解题思路:
- BFS 层级遍历,层级遍历,将当前层级中的所有节点值添加到一维数组中
- 如果当前层是奇数,将一维数组中的值顺序添加到返回值二维数组中
- 如果当前层是偶数,将一维数组中的值逆序 (反向) 添加到返回值二维数组中 (也就是先将数组反转,然后再添加到返回值二维数组中)
