LeetCode Binary Search 刷题模板
概述
从应用的角度进行分析,二分查找属于 “双指针” 类型子集,即使有了虽然有了标准的二分查找算法模板,但是 LeetCode 上面的二分查找相关题目不会让你直接套模板,依然需要在二分查找的基础之上 学习新的技巧: 巧妙的边界处理、题型变换 (如何将题型变换为二分查找)。
// Go 语言实现的二分查找算法
func binarySearch(nums []int, target int) int {
low, hi := 0, len(nums)-1
for low <= hi {
// 防止两数相加时溢出
mid := low + (hi-low)>>1
if nums[mid] == target {
return mid
} else if nums[mid] > target {
hi = mid - 1
} else {
low = mid + 1
}
}
return -1
}
珠玉在前,本文尝试在二分算法的技术上,从实用主义出发,通过刷题提升解题的速度,通过图解算法过程加深二分查找算法的理解。
二分查找,算法模板代码是基础,边界判断是玄学。
💡 典型题目
1. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。
# 示例来自: https://leetcode.cn/
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
题目是在有序数组中查找位置,并且要求算法时间复杂度为 O(N log N), 基本上就是告诉你要使用二分查找算法解题。
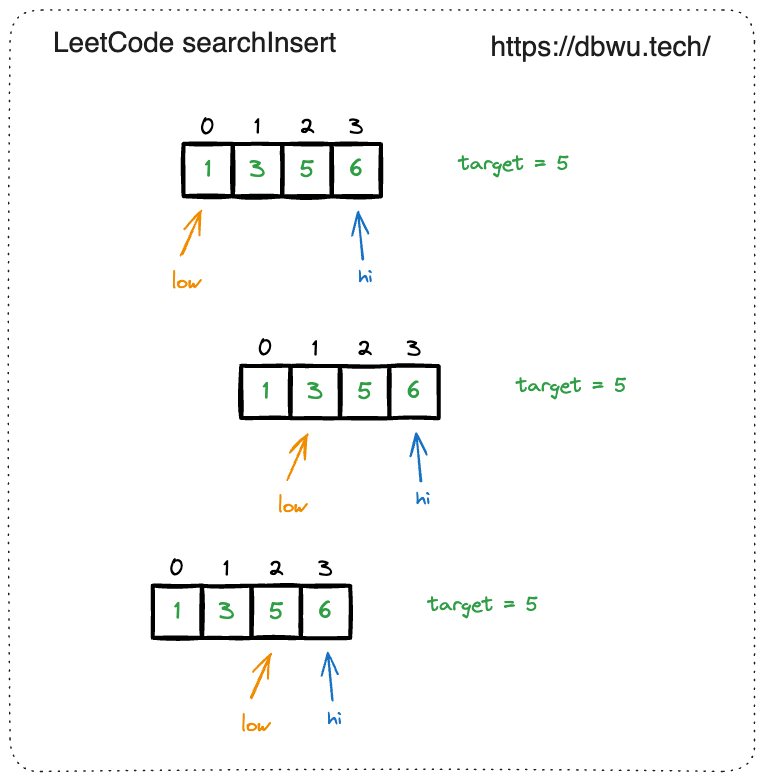
翻译后: 在一个有序数组中找到第一个大于等于 target 的索引位置。
直接将二分查找的算法的返回值修改一下,就是解题答案:
// 题解代码
func searchInsert(nums []int, target int) int {
low, hi := 0, len(nums)-1
for low <= hi {
mid := low + (hi-low)>>1
if nums[mid] == target {
// 找到目标值后直接返回索引
return mid
} else if nums[mid] >= target {
// target 在数组的左半部分
hi = mid - 1
} else {
// target 在数组的右半部分
low = mid + 1
}
}
// 如果没有找到目标值,直接将左边界返回
// 因为此时的数组以 low 位置切分为两部分:
// 1. 左半部分的元素全部比 nums[low] 小
// 2. 右半部分的元素全部比 nums[low] 大
// 索引 low 正好就是插入 target 目标元素的位置
return low
}
2. 搜索二维矩阵
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
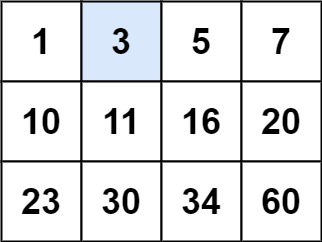
# 示例 1
target = 3, 返回 true
# 示例 2
target = 13, 返回 false
解题思路:
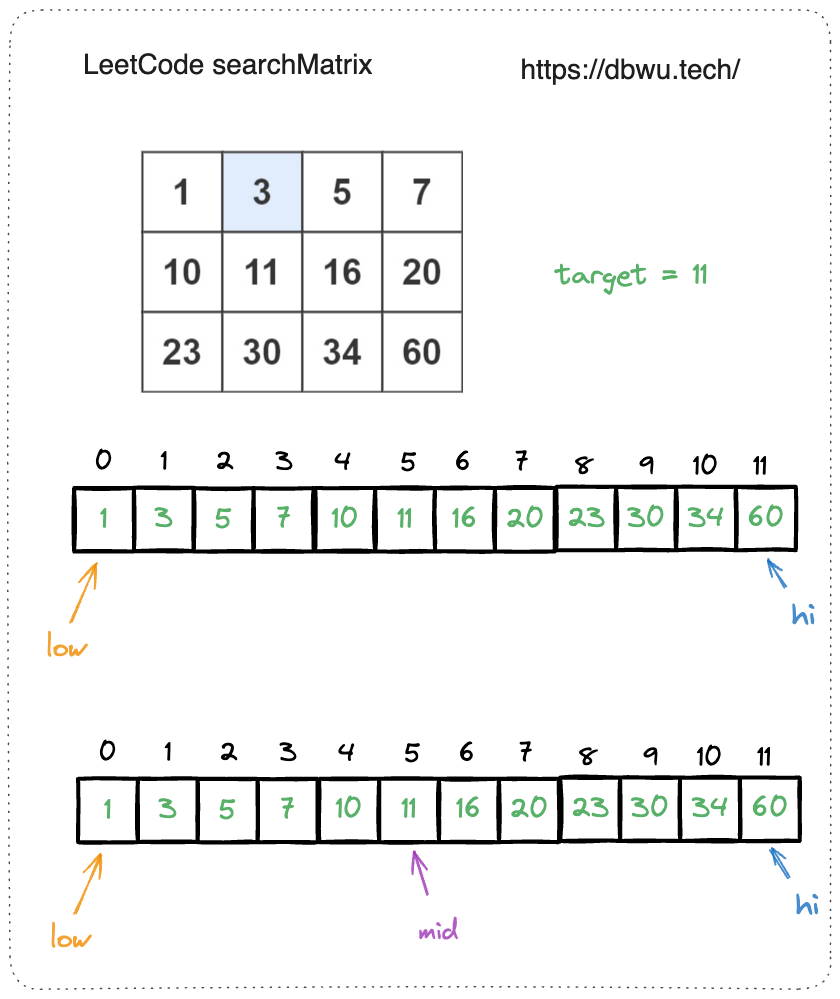
虽然题目中给的参数数据结构是矩阵,其实也就是二维数组,并且该二维数组是逐行逐列递增的,将其扁平化之后就是一个有序的一维数组,然后就可以套用二分查找算法来解题了。
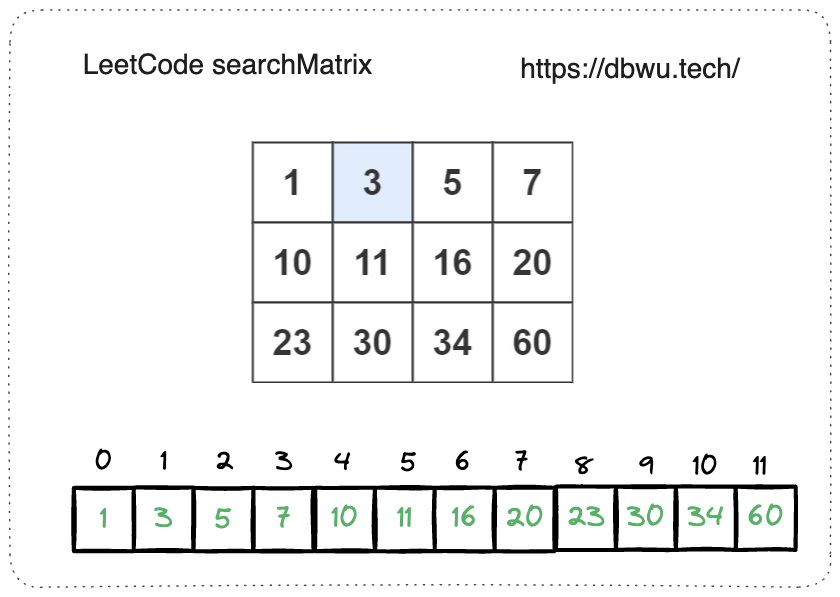
唯一需要注意的是: 二分查找过程中,需要将一维数组索引转化为对应矩阵(二维数组)的坐标。
// 题解代码
// 将矩阵每一行拼接在上一行的末尾,则会得到一个升序数组
// 可以在该数组上二分查找
func searchMatrix(matrix [][]int, target int) bool {
rows := len(matrix)
// 边界处理
if rows == 0 {
return false
}
cols := len(matrix[0])
// 一维数组的长度等于矩阵的行数量 * 列数量 - 1
// 因为数组下标从 0 开始
low, hi := 0, rows*cols-1
for low <= hi {
mid := low + (hi-low)>>1
// 将索引转换为具体的矩阵坐标
val := matrix[mid/cols][mid%cols]
if val == target {
return true
} else if val < target {
low = mid + 1
} else {
hi = mid - 1
}
}
return false
}
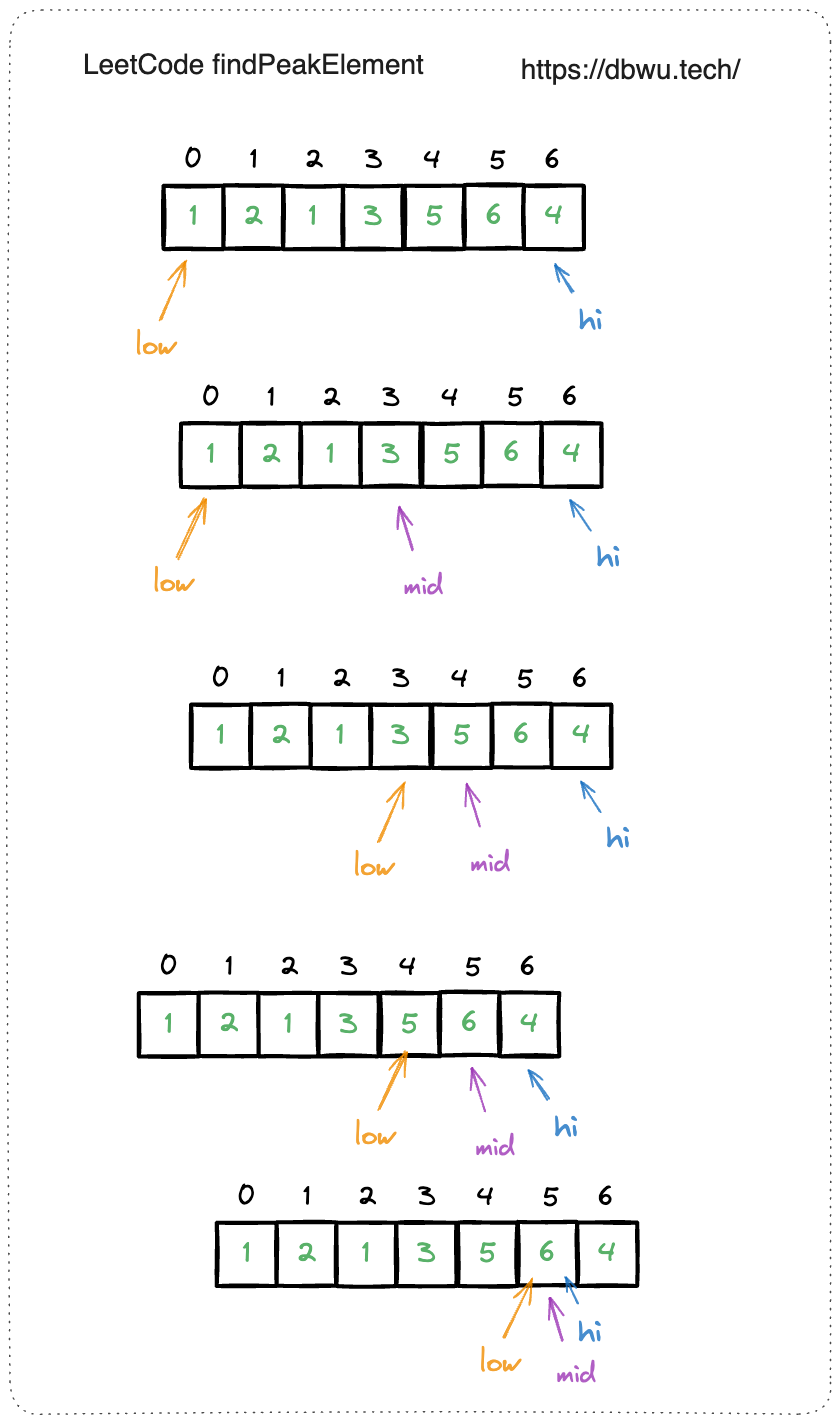
3. 寻找峰值
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。 峰值元素是指其值严格大于左右相邻值的元素。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
解题思路:
我们可以 在二分查找算法的基础上略微修改:每个二分查找过程中不再是查找具体的 target, 而是直接使用当前的 “中间元素” 为基准进行对比:
- 如果当前 “中间元素” 大于紧跟其后的元素,说明当前元素后面的元素不是峰值元素,此时可能存在两种情况:
- 当前元素是一个峰值元素
- 当前元素的左侧存在峰值元素
- 无论两种情况中的哪一种,直接将指向右侧边界的 hi 指针指向当前元素索引
- 如果当前 “中间元素” 小于等于紧跟其后的元素,说明当前元素后面存在峰值元素, 直接将指向左侧边界的 low 指针指向当前元素索引 + 1
// 题解代码
func findPeakElement(nums []int) int {
low, hi := 0, len(nums)-1
for low < hi {
mid := low + (hi-low)>>1
// 如果 mid 较大,则左侧存在峰值,high = m
// 如果 mid + 1 较大,则右侧存在峰值,low = mid + 1
if nums[mid] > nums[mid+1] {
hi = mid
} else {
low = mid + 1
}
}
return low
}
注意题解代码中和标准二分查找模板的细节差异,但从出题的角度分析,笔者认为这道题并没有前两道题有价值。
4. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
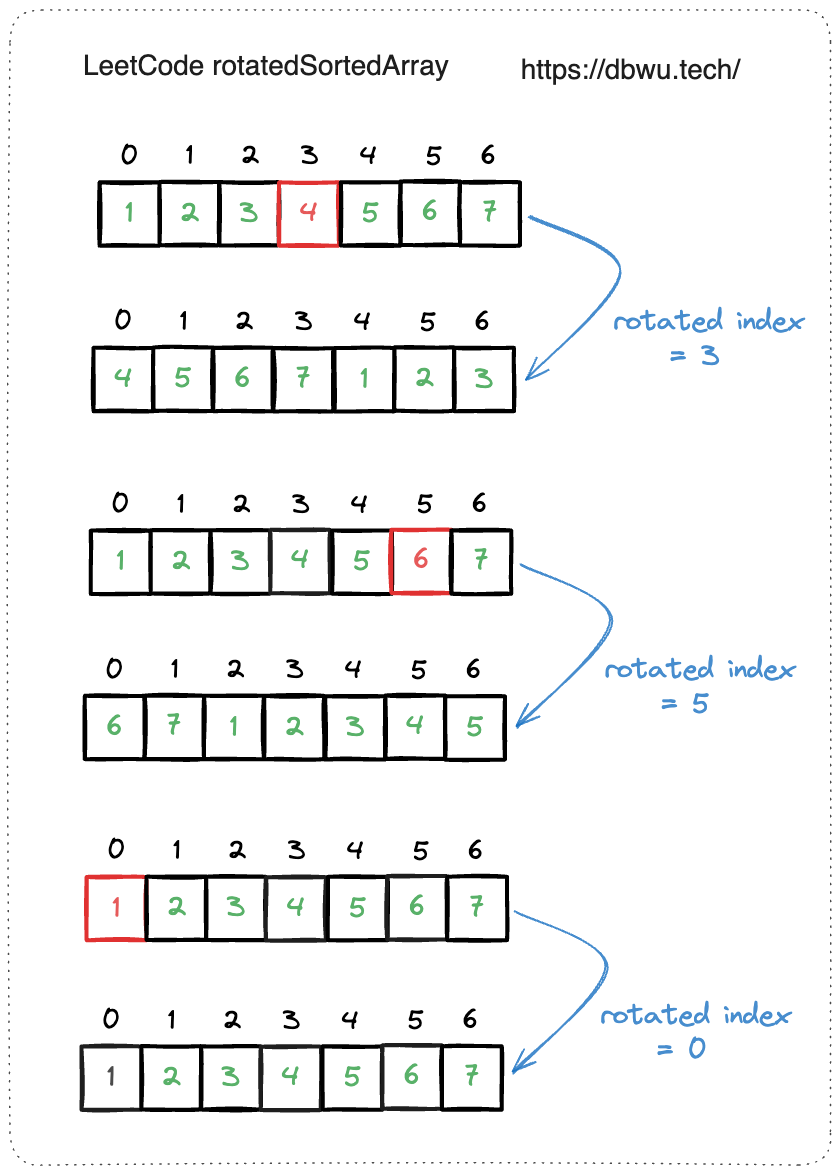
通过分析几个旋转后的数组图片,你会发现这道题本质上还是二分查找题,将旋转后的数组规律进行总结:
将旋转后的数组一分为二,其中一定有一个数组是有序的,另一个可能是有序数组,也能是部分有序的数组。
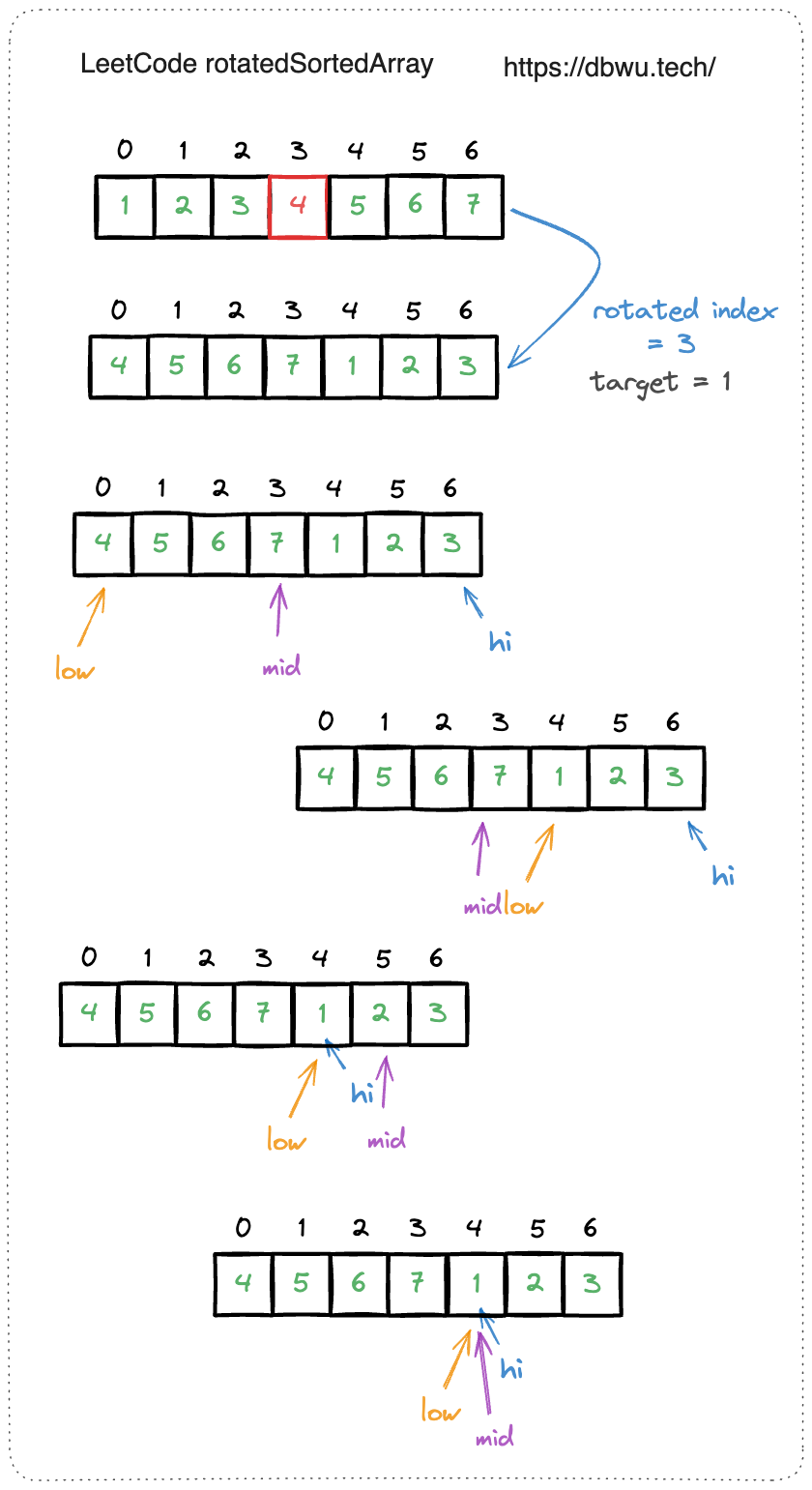
所以需要对标准的二分查找需要进行调整,具体来说:
- 如果当前元素正好等于要查找的目标元素 target, 直接返回当前元素的索引
- 如果以当前元素将数组分为两部分:
- 如果左半部分的所有元素都是有序的
- 如果要查找的元素所在于左半部分,将二分范围缩小到左半部分
- 否则将二分范围缩小到右半部分
- 如果左半部分的所有元素不是有序的
- 如果要查找的元素所在于右半部分,将二分范围缩小到右半部分
- 否则将二分范围缩小到左半部分
- 如果左半部分的所有元素都是有序的
// 题解代码
func search(nums []int, target int) int {
low, hi := 0, len(nums)-1
for low <= hi {
mid := low + (hi-low)>>1
if nums[mid] == target {
return mid
}
// 如果[low, mid - 1] 是有序数组
// 且 target 的大小满足 ([nums[low],nums[mid]) 则将搜索范围缩小至 [low, mid - 1]
// 否则在 [mid + 1, hi] 中寻找
// 通过区间左右两端的数字来确认该区间是否有序
if nums[low] <= nums[mid] {
if nums[low] <= target && target < nums[mid] {
hi = mid - 1
} else {
low = mid + 1
}
} else {
if nums[mid] < target && target <= nums[hi] {
low = mid + 1
} else {
hi = mid - 1
}
}
}
return -1
}
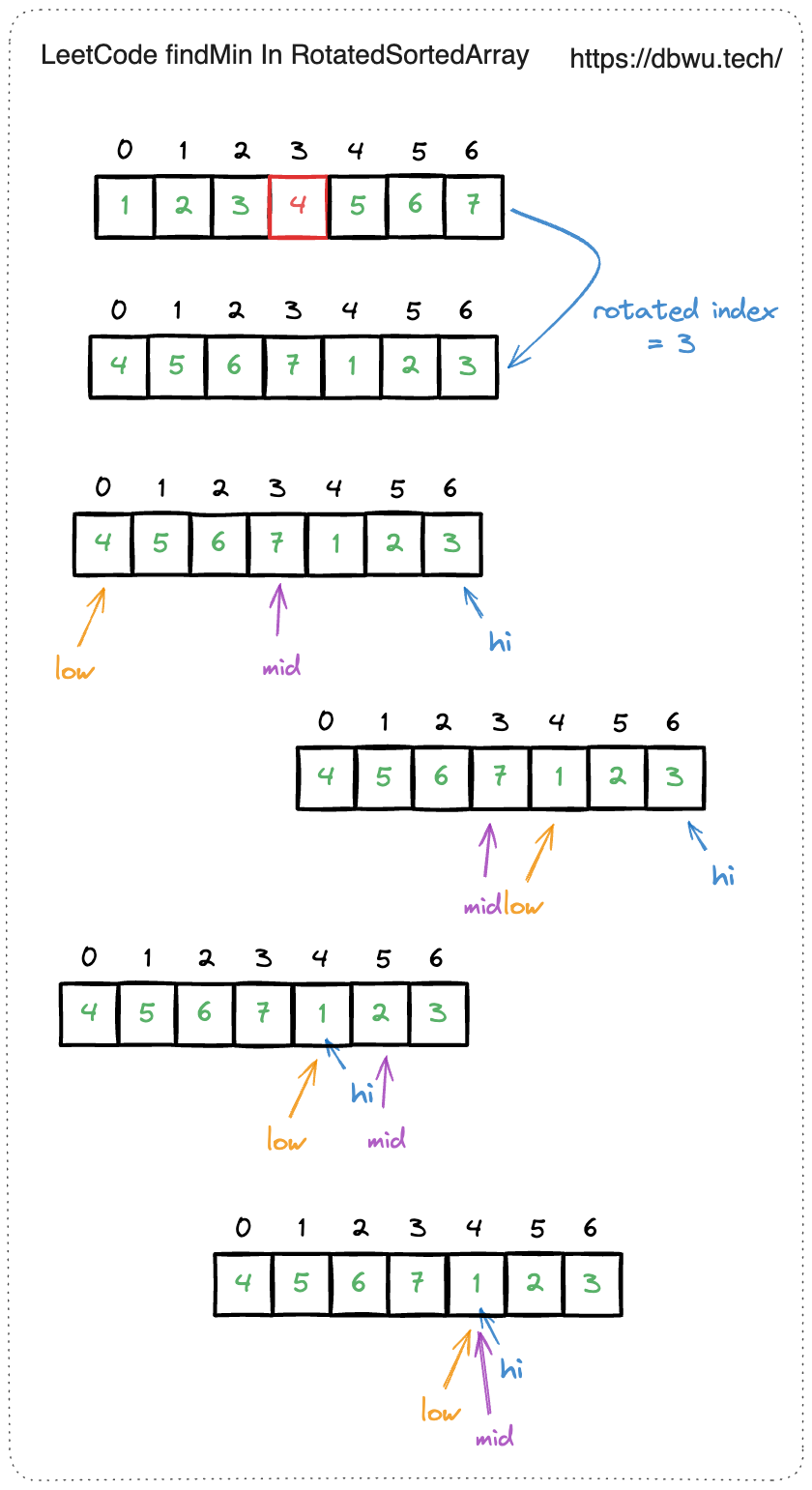
5. 寻找旋转排序数组中的最小值
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
依然是旋转数组,沿袭前面第 4 题的思路:
将旋转后的数组一分为二,其中一定有一个数组是有序的,另一个可能是有序数组,也能是部分有序的数组。
直接套用二分搜索模板: 每次二分搜索过程中取出中间元素: 如果中间元素小于右边界元素,说明最小元素位于左半部分,否则说明最小元素位于右半部分。
下面举一个简单的小例子来说明这个过程:
# 源数组
[0, 1, 2, 4, 5, 6, 7]
# 若旋转 4 次,则可以得到
[4, 5, 6, 7, 0, 1, 2]
# 此时中间元素为 7, 大于右边界的元素 2,所以最小元素位于右半部分
# 若旋转 7 次,则可以得到
[0, 1, 2, 4, 5, 6, 7]
# 此时中间元素为 4, 大于右边界的元素 7,所以最小元素位于左半部分
// 题解代码
func findMin(nums []int) int {
low, hi := 0, len(nums)-1
for low < hi {
mid := low + (hi-low)>>1
if nums[mid] < nums[hi] {
// 为什么 high = mid, 而不是 high = mid-1 ?
// 因为 nums[mid] 有可能就是最小值
// 示例: {4, 5, 1, 2, 3}
// 如果 high = mid - 1,则丢失了最小值 1
hi = mid
} else {
// 为什么 low = mid + 1, 而不是 low = mid ?
// 因为 nums[mid] 不可能是最小值
// 因为如果 nums[mid] 是最小值
// 那么其会满足上面的表达式: nums[mid] < nums[hi]
// 代码就不会执行到这里了
low = mid + 1
}
}
return nums[low]
}
💡 变通题目
1. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
表面看这是一道二分查找题,先找出目标元素 target 的第一个出现位置,然后找出最后一个出现位置,但是参数给出的是整数数组,所以其实可以将题目转换一下:
- 查找目标元素 target 的插入位置
- 查找目标元素 target+1 的插入位置,该位置正好就是 target 的最后一个出现位置
寻找目标元素插入位置,就是前文中的原题 (连套模板代码都不需要了,直接复制粘贴即可)。
// 题解代码
func searchRange(nums []int, target int) []int {
// 查找目标元素 target 的插入位置
left := search(nums, target)
// 查找目标元素 target+1 的插入位置
// 该位置正好就是 target 的最后一个出现位置
right := search(nums, target+1)
// 边界处理
if left == len(nums) || nums[left] != target {
return []int{-1, -1}
}
return []int{left, right - 1}
}
// 寻找目标元素插入位置
// 前文中的原题
func search(nums []int, target int) int {
low, hi := 0, len(nums)-1
for low <= hi {
mid := low + (hi-low)>>1
if nums[mid] >= target {
hi = mid - 1
} else {
low = mid + 1
}
}
return low
}
2. 数字 k 在数组中出现频次
给定一个长度为 n 的升序数组和一个非负数整数 k ,要求统计 k 在数组中出现的次数。

该题和上一道题本质上是同一道题,只需要稍微变换下:
- 查找目标元素 target 的插入位置
- 查找目标元素 target+1 的插入位置,该位置正好就是 target 的最后一个出现位置
出现频次 = 最后出现位置 - 第一次出现位置
