LeetCode Binary Search Tree 刷题模板
📖 概述
在计算机科学中,二叉搜索树(BST)也称为有序或排序二叉树,其中每个节点的值必须大于(或等于)其左子树中的任何值,同时小于(或等于)其右子树中的任何值。
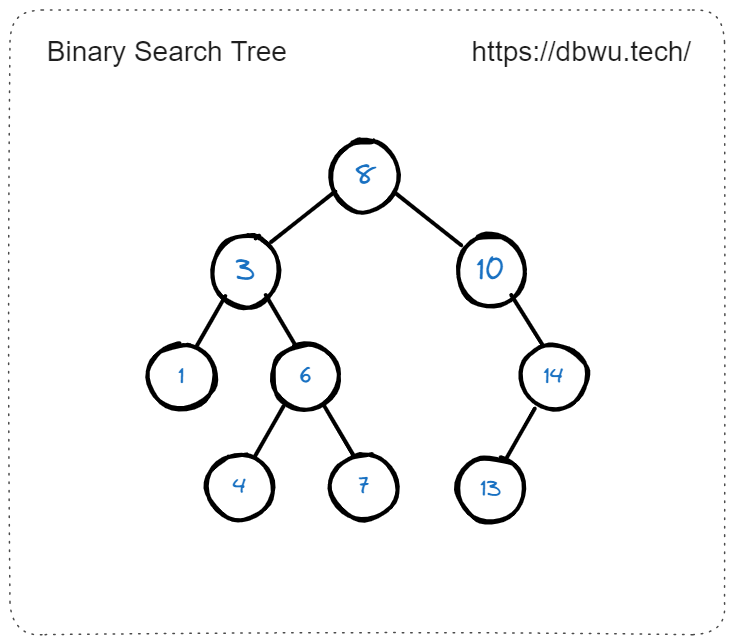
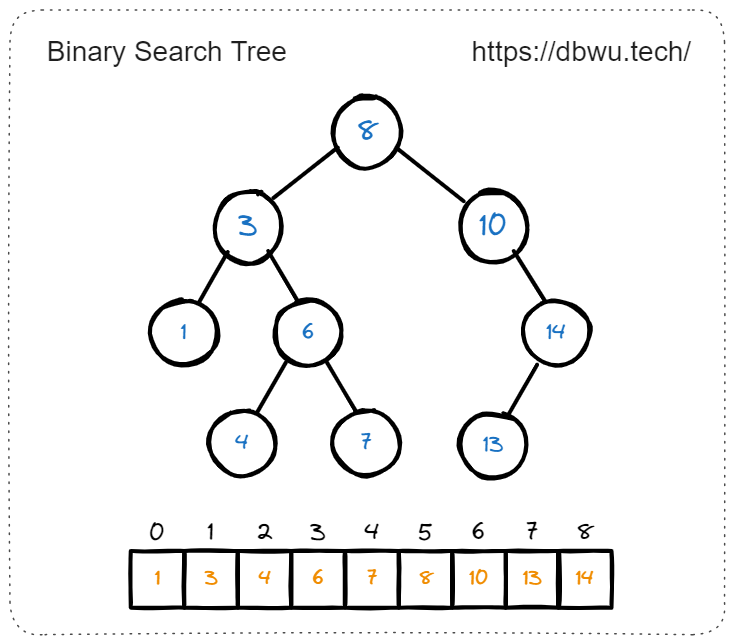
按照二叉搜索树的定义,使用 中序遍历 来访问树的各个节点,最终可以得到一个有序的数组。
刷题模板
LeetCode 中的二叉搜索树相关题目相对都比较简单,核心的解题思路就是充分利用二叉搜索树的有序性来完成对应的逻辑,这里直接给出一份基础模板代码,作用是通过中序遍历的方式来获取二叉搜索树的所有节点值 (已排序),读者可以在此模板代码上,根据不同的题来完成具体的逻辑部分代码,达到快速刷题的效果。
// 通过中序遍历获取二叉搜索树的所有节点值
func inorderTraversal(root *TreeNode) []int {
var res []int
var stack []*TreeNode
node := root
for node != nil || len(stack) > 0 {
for node != nil {
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
res = append(res, node.Val)
node = node.Right
}
return res
}
二叉树的脚手架代码可以使用之前 二叉树刷题模板中的脚手架代码 来辅助刷题和调试代码。
💡 典型题目
二叉搜索树中序遍历得到的值序列是递增有序的,因此这类问题的解决步骤一般是 中序遍历 + 具体处理逻辑,只要得到中序遍历后的值序列 (利用前文中提到的模板),就可以在此基础上快速解题。
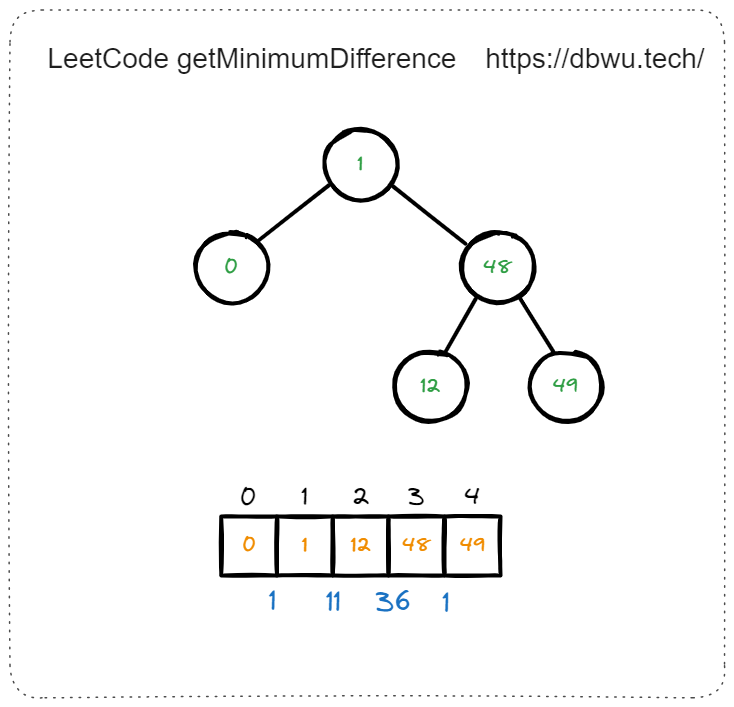
1. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
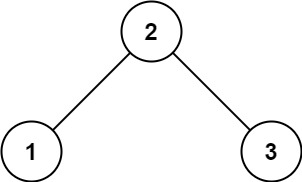
如图所示的二叉搜索树的最小差值为 1 (2 - 1 = 1)。
快速套解题模板:
- 最小绝对差来自于 离得最近的两个数
- 使用中序遍历获得二叉搜索树排序后的所有节点值
- 遍历所有节点值,挨个计算两个数之间的差值,同时更新这个过程中的最小差值
// 题解代码
func getMinimumDifference(root *TreeNode) int {
vals := inorderTraversal(root)
if len(vals) == 0 {
return -1
}
// 最小差值初始化为一个超大数
minDiff := math.MaxInt64
for i := 1; i < len(vals); i++ {
// 比较两个数的同时,更新最小差值
minDiff = min(minDiff, vals[i]-vals[i-1])
}
return minDiff
}
// 使用中序遍历获得二叉搜索树排序后的所有节点值
// 这里直接使用前文 刷题模板中 提供的方法
// 为了节省篇幅、折叠方法的具体实现
func inorderTraversal(root *TreeNode) []int {
...
}
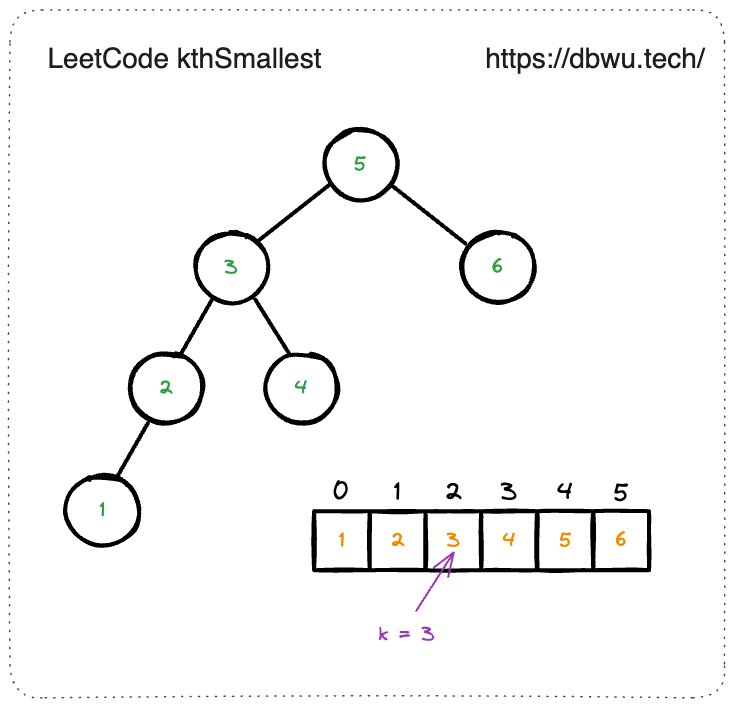
2. 二叉搜索树中第 K 小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
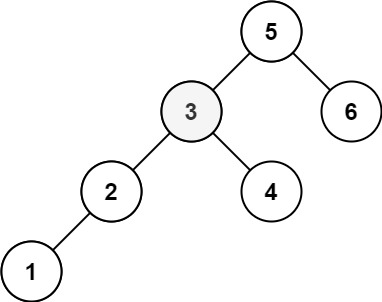
当 k = 3 时,最小的元素等于 3,数组排序后为 [1, 2, 3, 4, 5, 6]。
快速套解题模板:
- 使用中序遍历获得二叉搜索树排序后的所有节点值
- 获取第 k 个数字
这道题套上模板之后,简直就是送分题。
// 题解代码
func kthSmallest(root *TreeNode, k int) int {
nums := inorderTraversal(root)
return nums[k-1]
}
// 使用中序遍历获得二叉搜索树排序后的所有节点值
// 这里直接使用前文 刷题模板中 提供的方法
// 为了节省篇幅、折叠方法的具体实现
func inorderTraversal(root *TreeNode) []int {
...
}
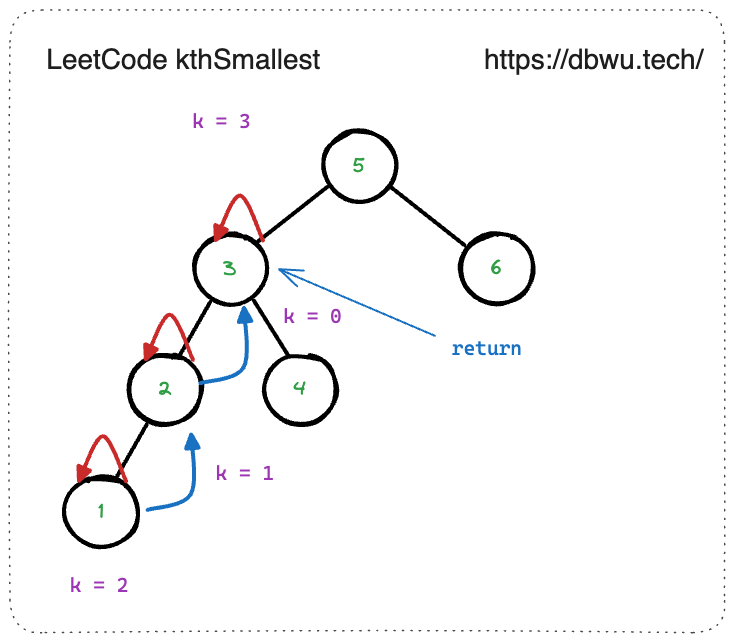
继续优化
上面的题解代码快速地解决了问题,因为仅仅在模板代码的基础上加了两行代码,但其实方法内部有额外的空间消耗,例如二叉搜索树有很多节点,但是这时参数 k 的值很小,上面的方法依然会遍历整棵二叉树才可以。
根据搜索二叉树的性质,当寻找第 k 个较小元素时,只需要使用中序遍历 (也就是按照节点值大小顺序遍历),遍历到第 k 的元素时,直接返回,这时就可以直接在模板代码的基础上进行修改。
// 优化题解代码
// 只需要在模板代码基础上修改即可
func kthSmallest(root *TreeNode, k int) int {
var stack []*TreeNode
for {
// 中序遍历顺序
// 1. 左子树
// 2. 根节点
// 3. 右子树
// 1. 左子树
for root != nil {
stack = append(stack, root)
root = root.Left
}
// 2. 根节点
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
// 每遍历一个数字时,将 k 减去 1
// 作用: 累加器
k--
if k == 0 {
// 当 k 等于 0 的时候
// 当前节点值就是整棵搜索二叉树中第 k 小的元素
return root.Val
}
// 右子树
root = root.Right
}
}
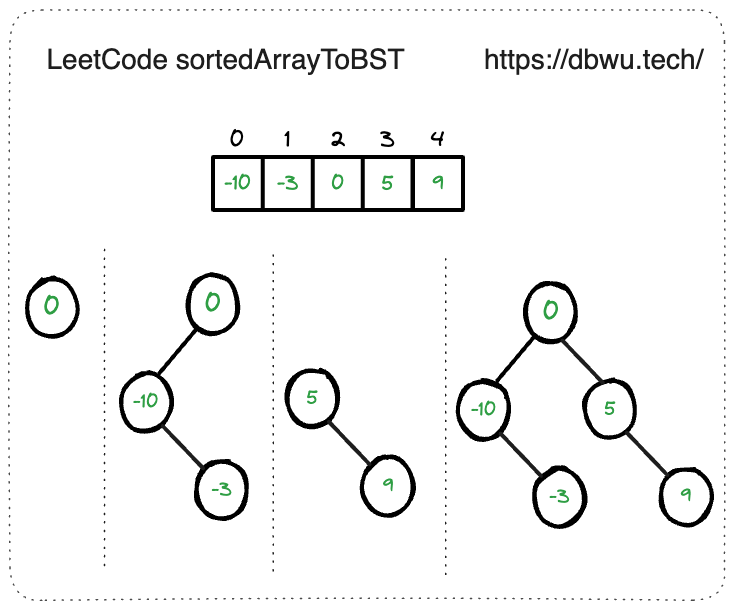
3. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 二叉搜索树。
解题思路:
这道题不需要查找求值,而是要构建二叉搜索树,所以前文中的刷题模板代码这里用不到。不过没关系,题目中给出的是已经排序完成的数组,根据二叉搜索树的性质,我们很容易通过分治 (递归) 的思路来解题:
- 将数组以中间的元素为基准,将数组分成 3 个部分: 左半部分、中间元素、右半部分
- 取出数组的中间元素作为根节点的值
- 将左半部分作为根节点的左子树 (递归调用)
- 将右半部分作为根节点的右子树 (递归调用)
- 返回根节点
// 题解代码
func sortedArrayToBST(nums []int) *TreeNode {
return build(nums, 0, len(nums)-1)
}
func build(nums []int, left, right int) *TreeNode {
if left > right {
return nil
}
// 将数组以中间的元素为基准,将数组分成 3 个部分: 左半部分、中间元素、右半部分
mid := left + (right-left) >> 1
// 取出数组的中间元素作为根节点的值
root := &TreeNode{Val: nums[mid]}
// 将左半部分作为根节点的左子树 (递归调用)
root.Left = build(nums, left, mid-1)
// 将右半部分作为根节点的右子树 (递归调用)
root.Right = build(nums, mid+1, right)
return root
}
💡 陷阱题
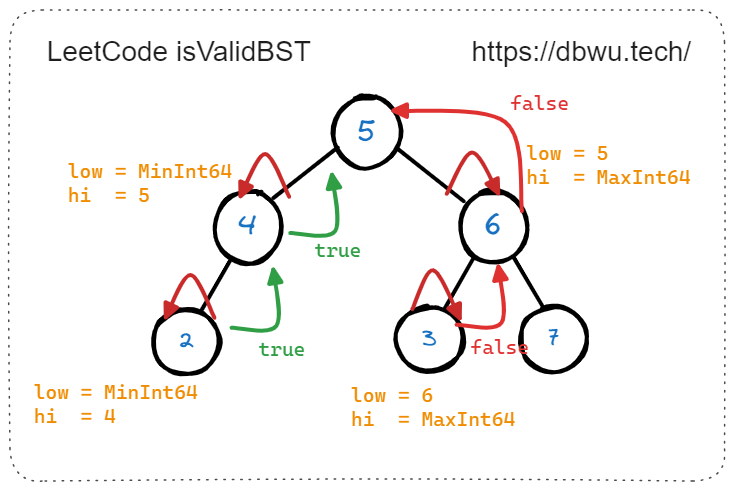
1. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。

如图所示的二叉树 是 二叉搜索树。
如图所示的二叉树 不是 二叉搜索树。
根据二叉搜索树的特征,出于直觉,我们很容易写出下面的递归代码:
func isValidBST(root *TreeNode) bool {
if root == nil {
return true
}
// 如果根节点的值小于等于左节点的值, 不符合二叉搜索树规则
if root.Left != nil && root.Val <= root.Left.Val {
return false
}
// 如果根节点的值大于等于右节点的值, 不符合二叉搜索树规则
if root.Right != nil && root.Val >= root.Right.Val {
return false
}
// 递归判断左节点和右节点是否为二叉搜索树
return isValidBST(root.Left) && isValidBST(root.Right)
}
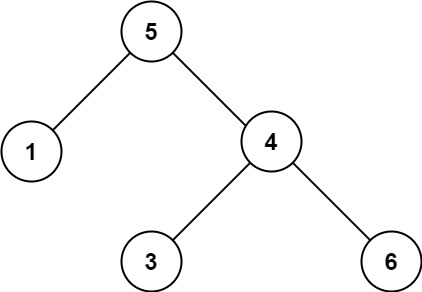
这里有个陷阱: 我们认为只要左右节点符合二叉搜索树特征,递归下去就可以判断整棵树是否符合二叉搜索树特征,但是 问题的根源在于 我们需要确认的不止是左右两个节点,而是左右两棵子树,所以上面的代码在这个测试用例中就会返回错误的结果。
5
/ \
4 6
/ \
3 7
上图所示的二叉树并不是二叉搜索树,但是代码依然会返回 true, 原因就在于代码只是检测了右节点和其两个子节点是否为二叉搜索树,但是并未检测整个右子树是否为二叉搜索树。
现在刚才的代码基础上进行修正,具体来说:
- 递归判断左子树时,除了判断 “当前节点值” 是否小于等于左节点值,还需要判断左子树中所有节点值是否小于整个树的根节点值
- 递归判断右子树时,除了判断 “当前节点值” 是否大于等于右节点值,还需要判断右子树中所有节点值是否大于整个树的根节点值
修正后的方法每次递归时需要两个基准边界值 (low, hi) 作为参数,当前节点的值必须 大于 low 并且小于 hi , 这样才符合二叉搜索树的特征,同时在向树的深层递归时更新 (low, hi) 参数值,具体来说:
- 递归判断左子树时,low 值保持不变,hi 值变为当前节点的值 (也就是说左节点及其子树中的所有节点值,都不能大于当前节点值)
- 递归判断左子树时,hi 值保持不变,low 值变为当前节点的值 (也就是说右节点及其子树中的所有节点值,都不能小于当前节点值)
为了可以 LeetCode 官方提供的函数原型上正常提交 AC,这里单独写一个方法作为 “辅助方法”,然后在原型方法中调用即可,最终修正后的代码如下。
func isValidBST(root *TreeNode) bool {
// 使用 64 位最小值和最大值来模拟 (low, hi) 左右边界值
return helper(root, math.MinInt64, math.MaxInt64)
}
func helper(root *TreeNode, low, hi int) bool {
if root == nil {
return true
}
// 题目要求:
// 节点的左子树只包含小于当前节点的数
// 节点的右子树只包含大于当前节点的数
if root.Val <= low || root.Val >= hi {
return false
}
return helper(root.Left, low, root.Val) && helper(root.Right, root.Val, hi)
}