LeetCode Binary Tree 刷题模板
📖 基础知识
在计算机科学中,二叉树是一种树形数据结构,其中每个节点最多有两个子节点,称为左子节点和右子节点。
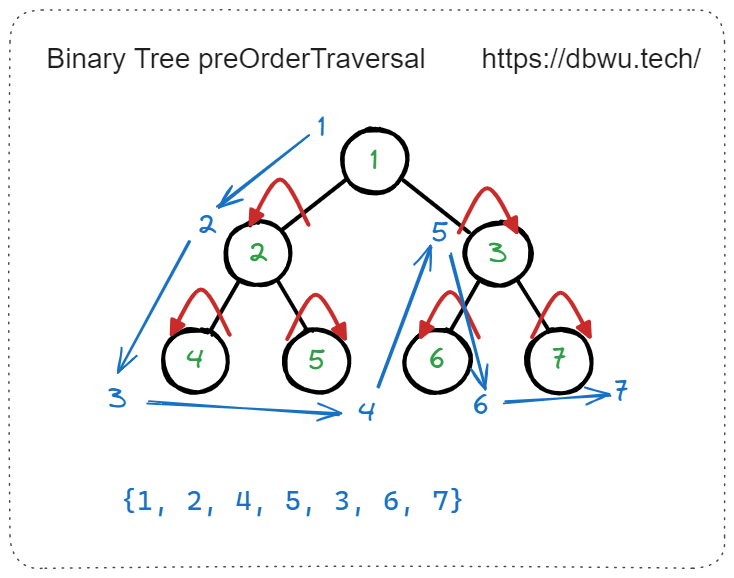
前序 (先序) 遍历
先访问根节点,然后 (递归) 前序遍历左子树,最后 (递归) 前序遍历右子树。
// 简单递归版本
func preOrderTraversal(root *TreeNode) {
if root != nil {
// 先访问根节点
fmt.Println(root.Val)
// 然后 (递归) 前序遍历左子树
preOrderTraversal(root.Left)
// 最后 (递归) 前序遍历右子树
preOrderTraversal(root.Right)
}
}
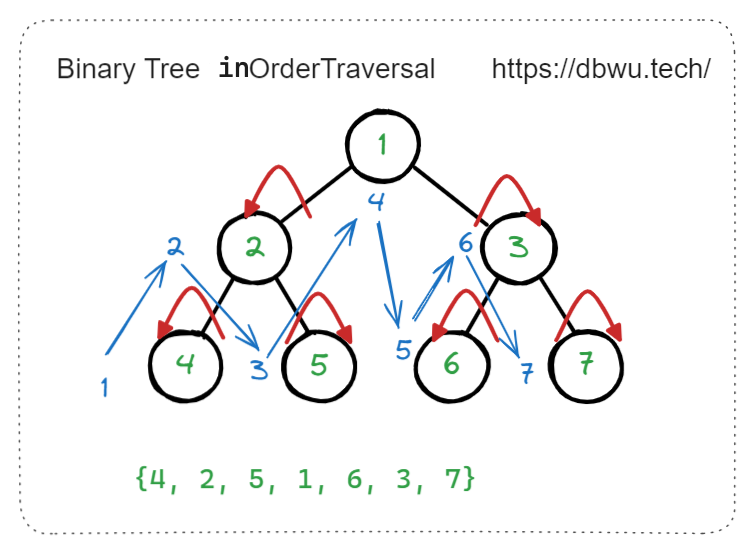
中序遍历
先 (递归) 中序遍历左子树,然后访问根节点,最后 (递归) 中序遍历右子树。
// 简单递归版本
func inOrderTraversal(root *TreeNode) {
if root != nil {
// 先 (递归) 中序遍历左子树
inOrderTraversal(root.Left)
// 然后访问根节点
fmt.Println(root.Val)
// 最后 (递归) 中序遍历右子树
inOrderTraversal(root.Right)
}
}
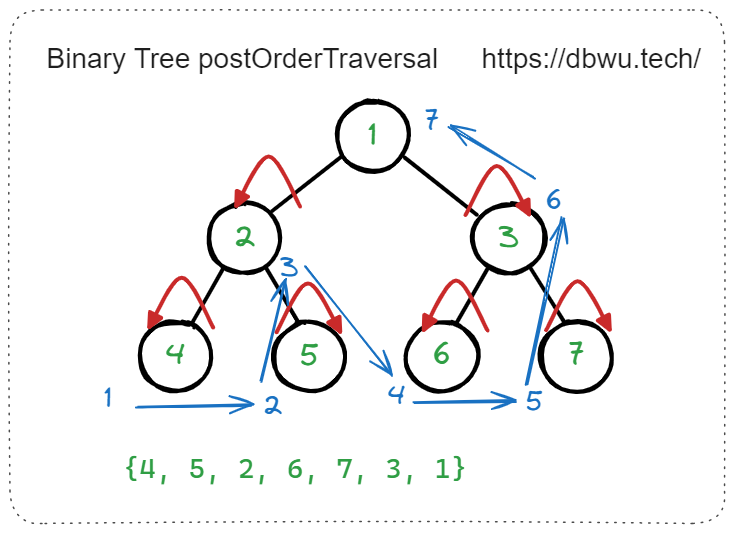
后序遍历
先 (递归) 后序遍历左子树,然后 (递归) 后序遍历右子树,最后访问根节点。
// 简单递归版本
func postOrderTraversal(root *TreeNode) {
if root != nil {
// 先 (递归) 后序遍历左子树
postOrderTraversal(root.Left)
// 然后 (递归) 后序遍历右子树
postOrderTraversal(root.Right)
// 最后访问根节点
fmt.Println(root.Val)
}
}
🛠️ 刷题脚手架
笔者根据 LeetCode 官方提供的 二叉树 数据结构,提供了两个简单的脚手架函数,用于快速生成测试和调试代码。
- 根据数组生成对应的二叉树结构,可以省去很多的重复性代码
- 打印指定二叉树,可以非常直观地看到当前二叉树的树形结构和各个节点的数据
因为二叉树相关的大部分题目都需要使用到递归,代码陷入递归后就会比较抽象,无法更加直观地了解当前程序执行状态,这时候就可以使用脚手架代码,打印出每次递归执行后的二叉树的树形结构和节点数据。
例如下边就是一个二叉树的打印后显示,可以根据输出的字符,非常直观地看到二叉树的结构和节点数据。
1
/ \
2 3
/ \
4 5
/ \
6 7
根据数组 (切片) 生成二叉树
// Tree 节点表示
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// 使用 math.MinInt64 来表示 NULL 节点的值
var NULL = math.MinInt64
func GenerateTreeNodesBySlice(nums []int) *TreeNode {
n := len(nums)
if n == 0 {
return nil
}
root := &TreeNode{Val: nums[0]}
queue := make([]*TreeNode, 1, n>>1+1)
queue[0] = root
for top, index := 0, 1; index < n; index++ {
node := queue[top]
top++
if nums[index] != NULL {
node.Left = &TreeNode{Val: nums[index]}
queue = append(queue, node.Left)
}
index++
if index < n && nums[index] != NULL {
node.Right = &TreeNode{Val: nums[index]}
queue = append(queue, node.Right)
}
}
return root
}
GenerateTreeNodesBySlice 方法用于将指定的切片转换为对应的二叉树结构,注意切片中的数据顺序和二叉树的层级遍历顺序是一致的,这样调用起来更简单,例如按照如下的参数进行调用:
root := GenerateTreeNodesBySlice([]int{1, 2, 3, NULL, NULL, 4, 5, NULL, NULL, 6, 7})
那么将会生成如下图片所示的二叉树:
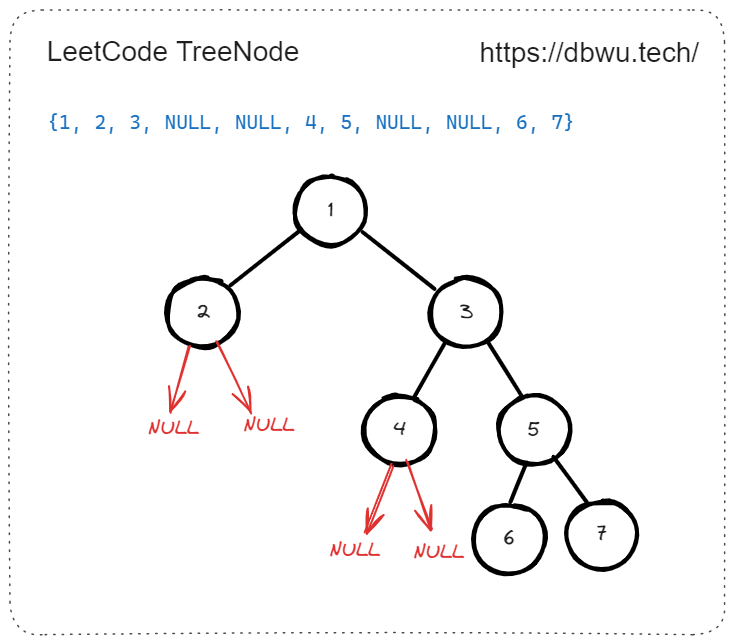
打印二叉树
func DumpTree(root *TreeNode) {
if root == nil {
return
}
// 保存需要打印的数字列表
levelRows := make([][]int, 0)
levelRows = append(levelRows, []int{root.Val})
// 使用 BFS 逐层组装数据
queue := []*TreeNode{root}
for len(queue) > 0 {
length := len(queue)
row := []int{}
// 从上一层数据中先填充当前层 NULL 数据
if len(levelRows) > 1 {
for _, val := range levelRows[len(levelRows)-1] {
if val != NULL {
break
}
// 上一层的 NULL 节点对应当前层的两个 NULL 子节点
row = append(row, NULL)
}
}
for i := 0; i < length; i++ {
if queue[i].Left != nil {
queue = append(queue, queue[i].Left)
row = append(row, queue[i].Left.Val)
} else {
row = append(row, NULL)
}
if queue[i].Right != nil {
queue = append(queue, queue[i].Right)
row = append(row, queue[i].Right.Val)
} else {
row = append(row, NULL)
}
}
levelRows = append(levelRows, row)
queue = queue[length:]
}
dumpTreeFormat(levelRows)
}
func dumpTreeFormat(valList [][]int) {
// 打印树形结构
width := len(valList)
for i := range valList {
// 填充左侧空格
for j := 0; j < width-i-1; j++ {
fmt.Printf(" ")
}
// 从第二层开始
// 需要填充上下连接符
if i > 0 {
for j := range valList[i] {
if valList[i][j] == NULL {
fmt.Printf(" ")
} else {
if j&1 == 0 {
fmt.Printf(" / ")
} else {
fmt.Printf("\\ ")
}
}
}
fmt.Println()
// 填充下一行数字的左侧空格
for j := 0; j < width-i-1; j++ {
fmt.Printf(" ")
}
}
// 填充数字
for j := range valList[i] {
if valList[i][j] == NULL {
fmt.Printf(" ")
} else {
fmt.Printf("%d ", valList[i][j])
}
}
fmt.Println()
}
}
DumpTree 方法打印指定的二叉树结构,注意切片中的数据顺序和二叉树的层级遍历顺序是一致的,这样调用起来更简单,例如按照如下的参数进行调用:
root := GenerateTreeNodesBySlice([]int{1, 2, 3, NULL, NULL, 4, 5, NULL, NULL, 6, 7})
DumpTree(root)
将会打印出如下所示的二叉树结构:
1
/ \
2 3
/ \
4 5
/ \
6 7
💡 典型题目 (构建二叉树)
前文中提到了二叉树的前序 (先序)、中序、后序遍历方式和对应的实现代码 (递归版本),LeetCode 中有专门针对这个知识点的题目,即根据某种遍历结果来反向构建对应的二叉树。
想要解决此类题目,必须对前序、中序、后序遍历三种遍历方式聊熟于心。
1. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出如下所示的二叉树结构
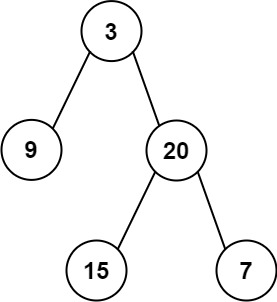
解题思路:
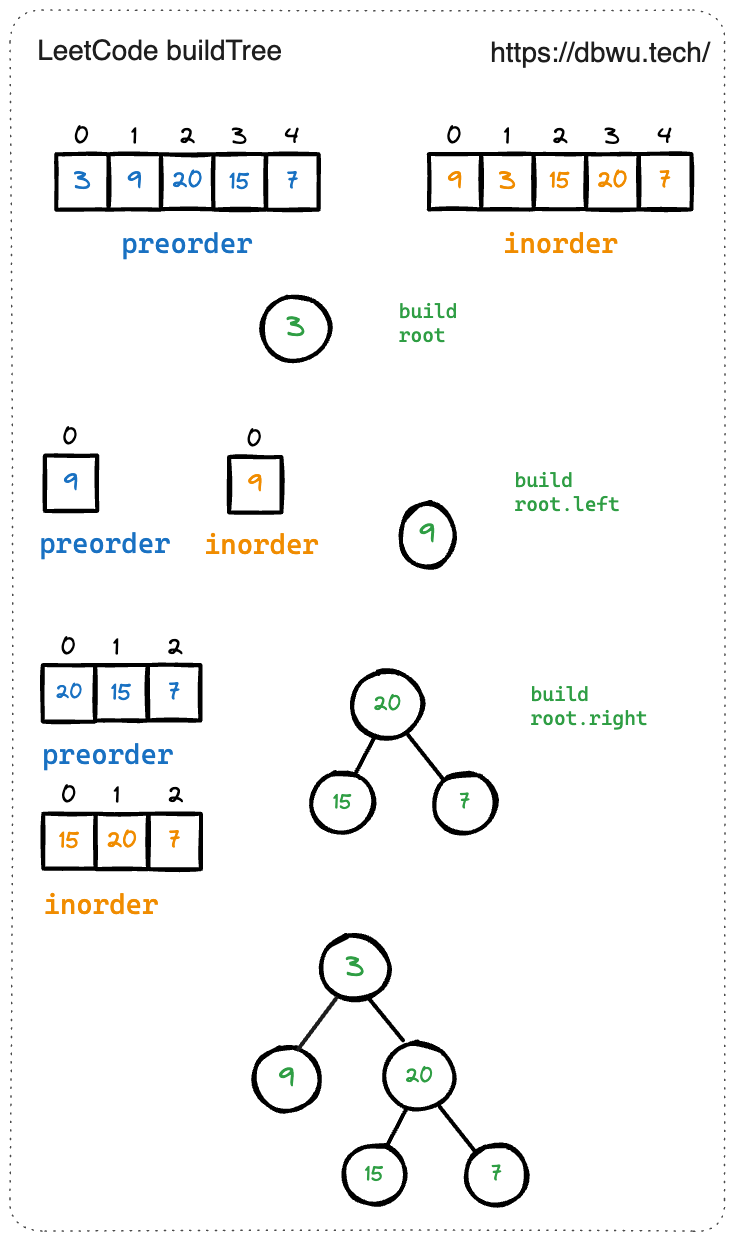
- 根据题目给出的两种遍历方式计算出根节点,前序遍历数组的第一个元素就是根节点
- 找到 中序遍历数组中根节点的值对应的索引,并根据索引将数组分成两个部分,左半部分就是左子树的所有节点值,右半部分就是右子树的所有节点值
- 递归数组左半部分,并将返回值赋值给 根节点的左节点
- 递归数组右半部分,并将返回值赋值给 根节点的右节点
// 题解代码
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder) == 0 {
return nil
}
// 前序遍历数组的第一个元素就是根节点
root := &TreeNode{Val: preorder[0]}
for i := range inorder {
// 找到中序遍历数组中根节点的值对应的索引
// 并根据索引将数组分成两个部分
if inorder[i] == root.Val {
// 左半部分就是左子树的所有节点值
root.Left = buildTree(preorder[1:i+1], inorder[:i])
// 右半部分就是右子树的所有节点值
root.Right = buildTree(preorder[i+1:], inorder[i+1:])
}
}
return root
}
2. 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
输入: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出如下所示的二叉树结构

解题思路:
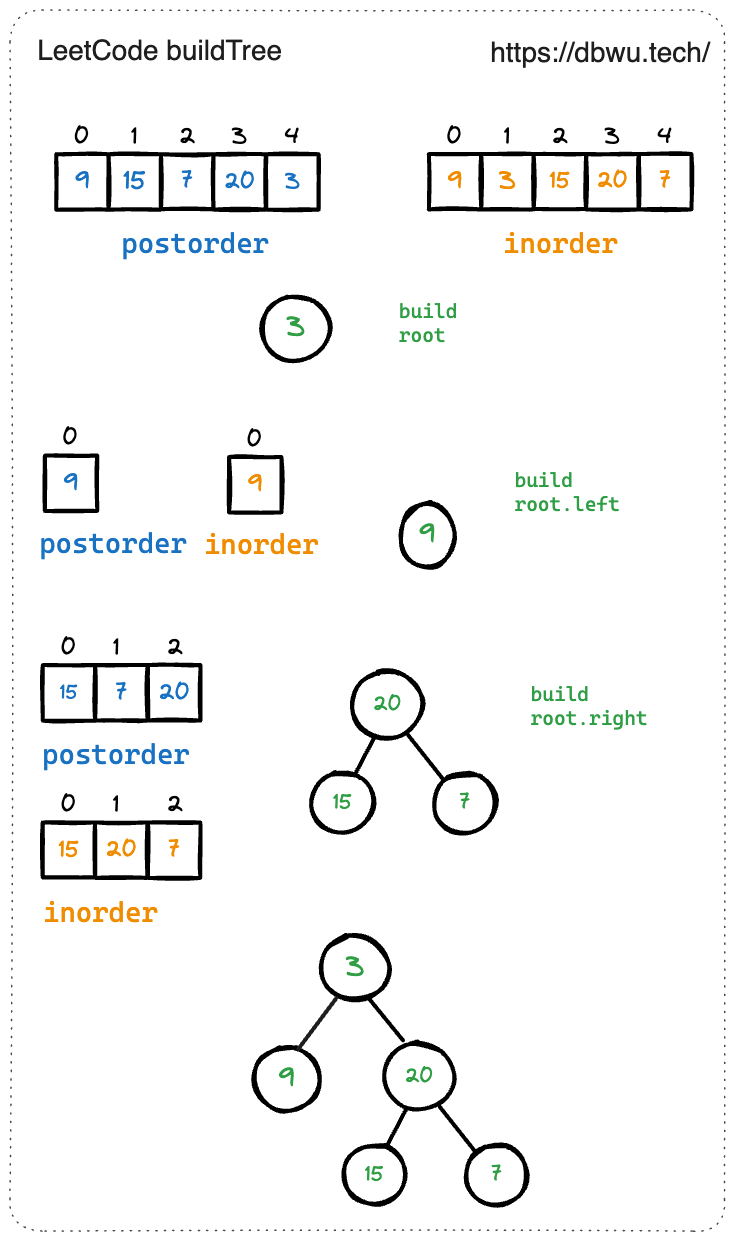
- 根据题目给出的两种遍历方式计算出根节点,后序遍历数组的最后一个元素就是根节点
- 找到 中序遍历数组中根节点的值对应的索引,并根据索引将数组分成两个部分,左半部分就是左子树的所有节点值,右半部分就是右子树的所有节点值
- 递归数组左半部分,并将返回值赋值给 根节点的左节点
- 递归数组右半部分,并将返回值赋值给 根节点的右节点
// 题解代码
func buildTree(inorder []int, postorder []int) *TreeNode {
n := len(postorder)
if n == 0 {
return nil
}
// 后序遍历数组的最后一个元素就是根节点
root := &TreeNode{Val: postorder[n-1]}
// 删除最后一个元素 (因为已使用)
postorder = postorder[:n-1]
for i := range inorder {
// 找到中序遍历数组中根节点的值对应的索引
// 并根据索引将数组分成两个部分
if inorder[i] == root.Val {
// 左半部分就是左子树的所有节点值
root.Left = buildTree(inorder[:i], postorder[:i])
// 右半部分就是右子树的所有节点值
root.Right = buildTree(inorder[i+1:], postorder[i:])
}
}
return root
}
🤔 思考题
根据先序遍历和后序遍历顺序是否可以确定出二叉树的结构?为什么?
根据先序和后序遍历的结果无法唯一确定二叉树,因为先序遍历和后序遍历序列无法提供足够的信息来唯一确定一棵二叉树。
具体来说:
- 如果只给出先序遍历序列,无法确定左右子树的分界线
- 如果只给出后序遍历序列,同样无法确定左右子树的分界线
- 如果同时给出先序遍历和后序遍历序列,依然无法唯一确定二叉树的结构。因为在这种情况下,可以构造出多个不同的二叉树,它们具有相同的先序和后序遍历序列。
举个例子:
下面同时给出了先序遍历和后序遍历序列的结果,但是该结果可以对应多棵二叉树结构。
# 先序遍历结果
preorder = [1, 2, 3]
# 后序遍历结果
postorder = [3, 2, 1]
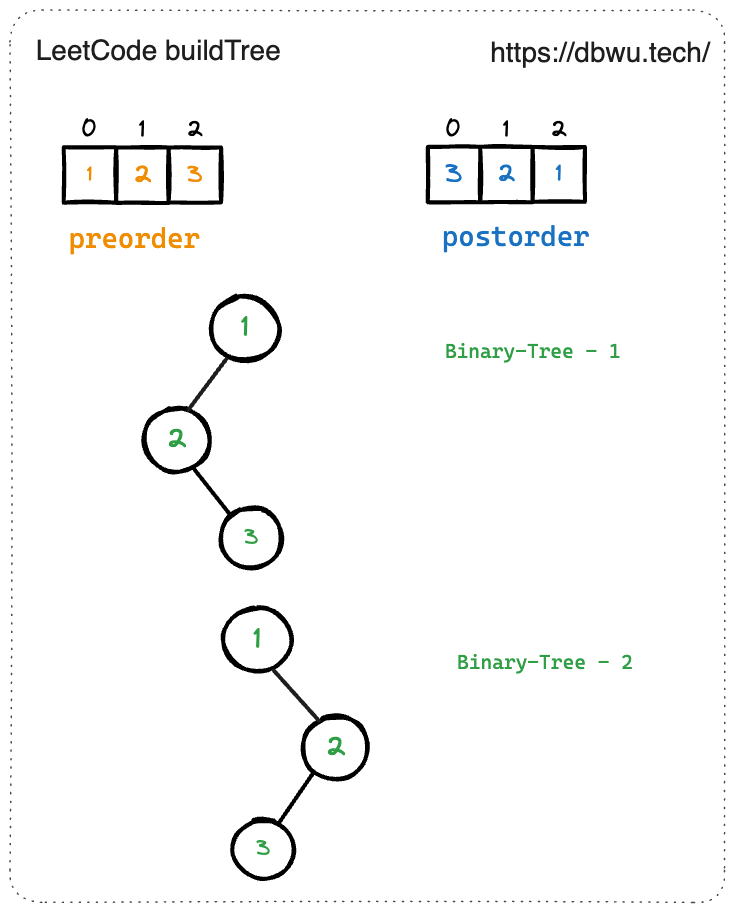
当二叉树的节点存在单个叶子节点的时候,无法唯一确定二叉树的结构。
📖 分治算法
在计算机科学中,分治法是一种很重要的算法,字面上的解释是 “分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题… 直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
分治算法是很多高效算法的实现基础,例如排序算法中的快速排序和归并排序、傅立叶变换 (快速傅立叶变换) 等。
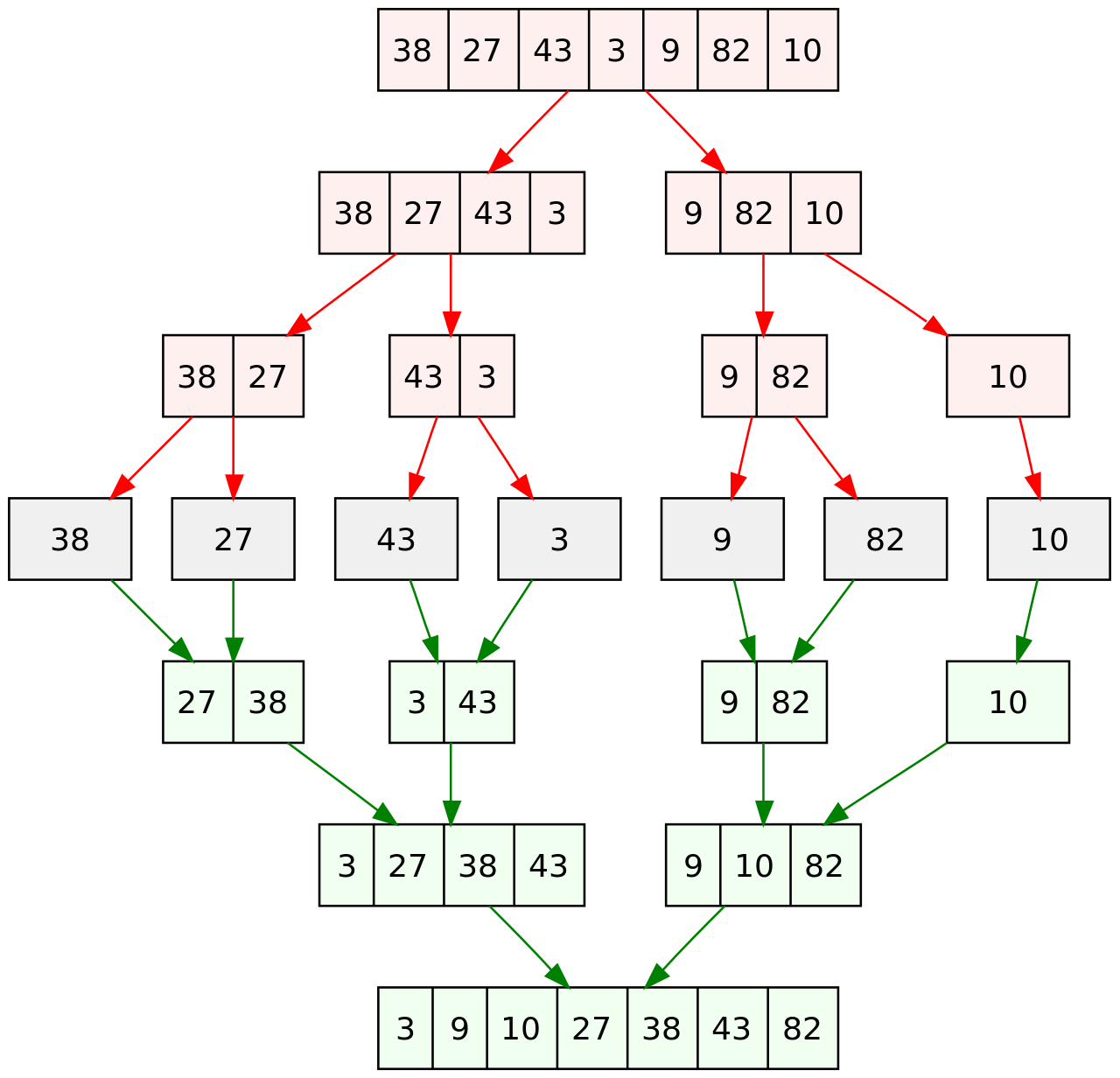
分治算法会将原问题不断拆分为子问题,然后循环往复,这 和递归的过程很像,事实上,大多数分治算法的实现都是递归,虽然使用迭代方法也可以实现对应的版本,但是代码量相比递归版本要多出很多,而且没有明显的性能优势。
二叉树的特征为每个节点有左右两颗子树,非常适合用分治算法进行遍历和求解相关操作,事实上,前文中提到的二叉树的三种遍历方式 (前序、中序、后序),均是使用分治 (递归) 实现的,从最终的实现代码来看,分治算法非常容易理解而且代码量很少、可读性很高。
刷题模板
解题思路:
- 识别递归边界
- 递归左子树计算出结果
- 递归右子树计算出结果
- 每个递归内部:对左子数的结果和右子树的结果进行计算并返回,或执行某些具体的操作
// LeetCode 二叉树刷题模板代码
func Solution(root *TreeNode) {
// 终止条件
if root == nil {
return
}
divideConquer(root)
}
// 分治递归处理左右子树
func divideConquer(root *TreeNode) {
// 终止条件
if root == nil {
// 处理空节点的情况
// 返回空值或特定值
...
return
}
// 递归左子树
leftResult := divideConquer(root.Left)
// 递归右子树
rightResult := divideConquer(root.Right)
// 处理递归后的左右子树结果
...
return
}
只要将解题思路分析清楚,然后确认好递归退出边界,填充具体的处理逻辑,大部分的二叉树题都在 10 行代码左右。
💡 典型题目 (分治)
1. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
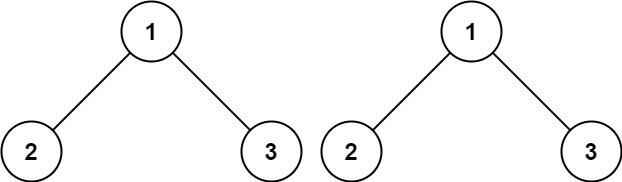
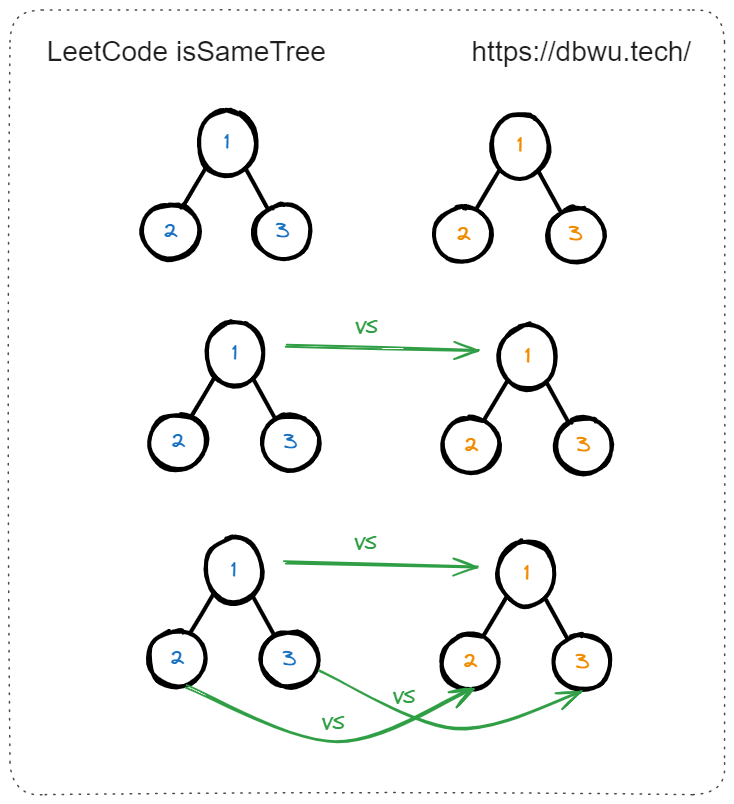
如图所示的两棵二叉树是相同的。
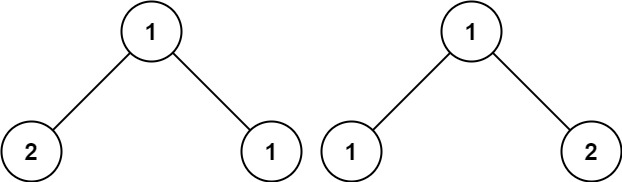
如图所示的两棵二叉树不相同。
解题思路:
- 识别递归边界: 左子树和右子树对应的任意两个节点不相同 (值不相等或者任一节点为 nil), 直接返回 false
- 递归判断两棵树的左子树是否相同
- 递归判断两棵树的右子树是否相同
- 如果左子数和右子树都相等,返回 true, 否则返回 false
// 题解代码
func isSameTree(p *TreeNode, q *TreeNode) bool {
if p == nil && q == nil {
return true
}
if p == nil || q == nil {
return false
}
return p.Val == q.Val && isSameTree(p.Left, q.Left) && isSameTree(p.Right, q.Right)
}
2. 翻转二叉树
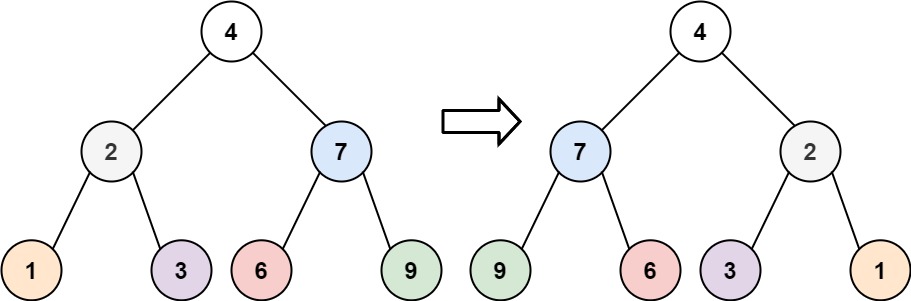
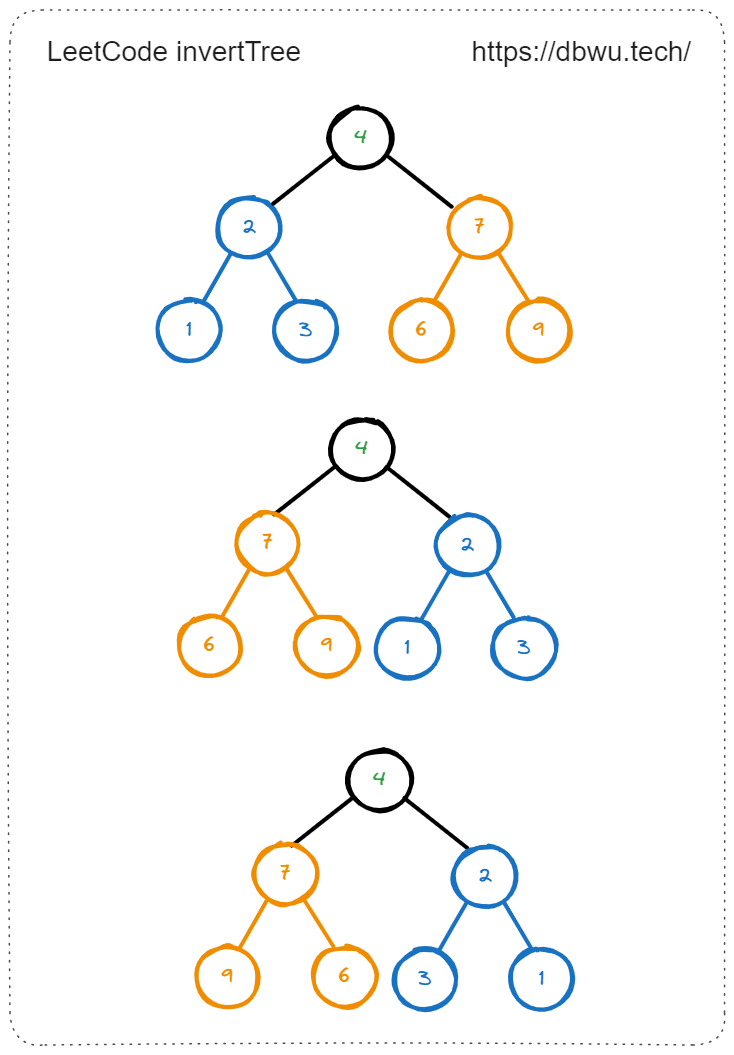
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
Homebrew(简称brew)是一个用于在 macOS 和 Linux 上安装软件包的包管理器,其作者去 Google 面试时,因为写不出来这道翻转二叉树算法题而遭到了拒绝。这本是一个面试官放水,求职者水过的喜剧片,却被主角来了一个神转折。

解题思路:
- 识别递归边界: 如果节点为 nil, 直接返回
- 交换当前节点的左右两个子节点
- 递归翻转左子树
- 递归翻转右子树
// 题解代码
func invertTree(root *TreeNode) *TreeNode {
if root == nil {
return root
}
// 交换当前节点的左右两个子节点
root.Left, root.Right = root.Right, root.Left
// 递归翻转左子树
invertTree(root.Left)
// 递归翻转右子树
invertTree(root.Right)
return root
}
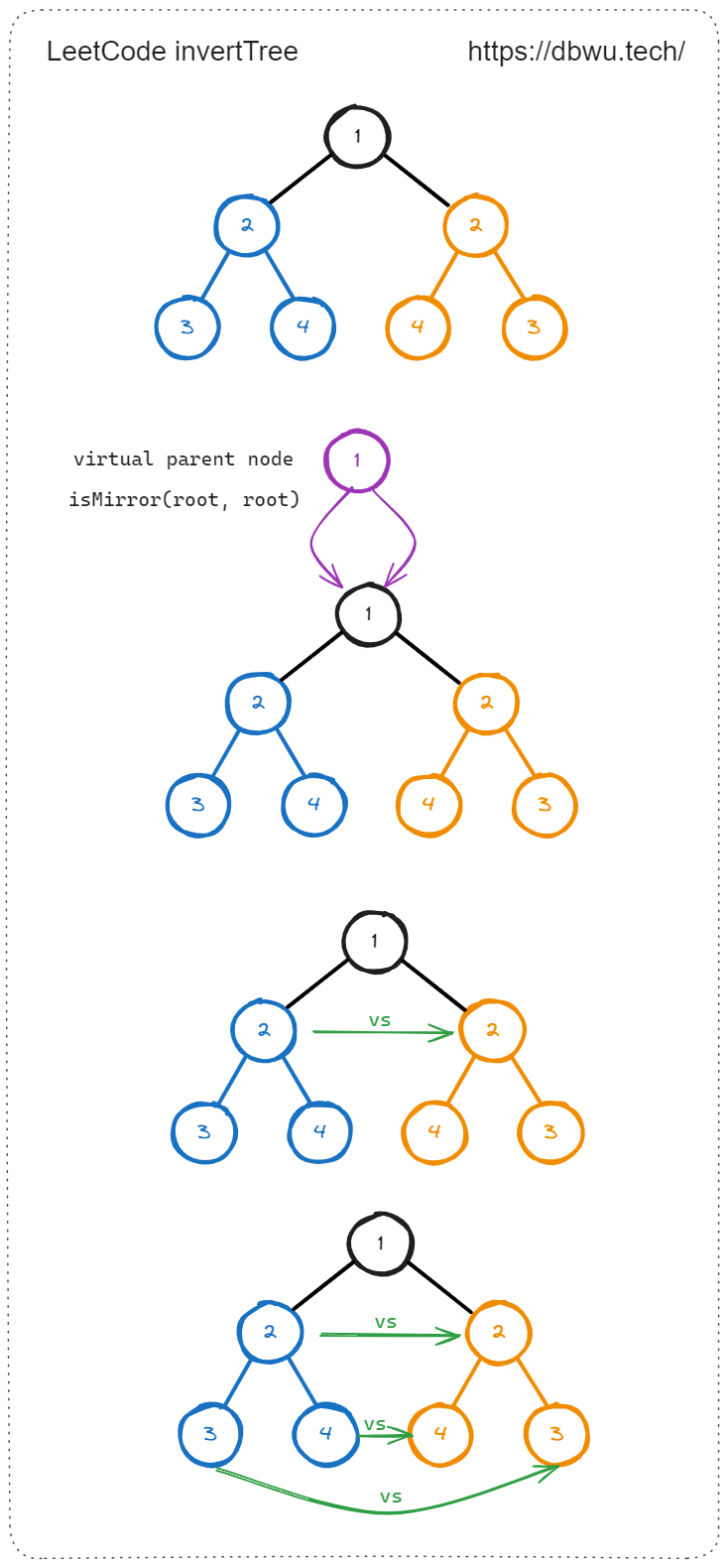
3. 对称二叉树
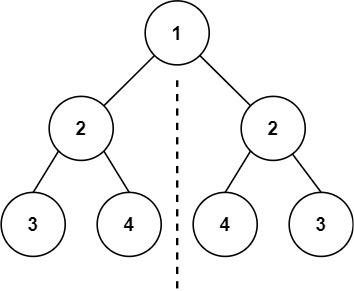
给你一个二叉树的根节点 root , 检查它是否轴对称。
下面是一个典型的对称二叉树示例。
解题思路:
- 识别递归边界: 如果 左子树的右节点 和 右子树的左节点 不相同,或者 左子树的左节点 和 右子树的右节点 不相同, (值不相等或者任一节点为 nil), 直接返回 false
- 递归检测 左子树的右节点 和 右子树的左节点 是否为镜像 (对称)
- 递归检测 左子树的左节点 和 右子树的右节点 是否为镜像 (对称)
- 如果两个节点的值相等,返回 true, 否则返回 false
和前面两个题稍微有点区别,因为在递归中单次需要判断的两个节点,分别位于左子树和右子树上,需要这里单独设计了一个辅助函数,函数的原型参数为设计为两个节点, 这样就可以传入 [左子树的右节点] + [右子树的左节点] 和 [左子树的左节点] + [右子树的右节点] 两种组合。
那么 root 这个特殊的单独节点如何处理呢?我们可以想象 root 节点还有一个虚拟的父节点,这个虚拟的父节点有左右两个子节点全部指向的是 root 节点,所以只需要将 root 作为辅助函数的参数传入两次即可,这样当辅助函数第一次进入递归调用时,就从 root 节点的下一层节点开始检测 (也就是整颗树的第二层)。
// 题解代码
func isSymmetric(root *TreeNode) bool {
return isMirror(root, root)
}
// 辅助函数
func isMirror(p, q *TreeNode) bool {
if p == nil && q == nil {
return true
}
if p == nil || q == nil {
return false
}
return p.Val == q.Val && isMirror(p.Left, q.Right) && isMirror(p.Right, q.Left)
}
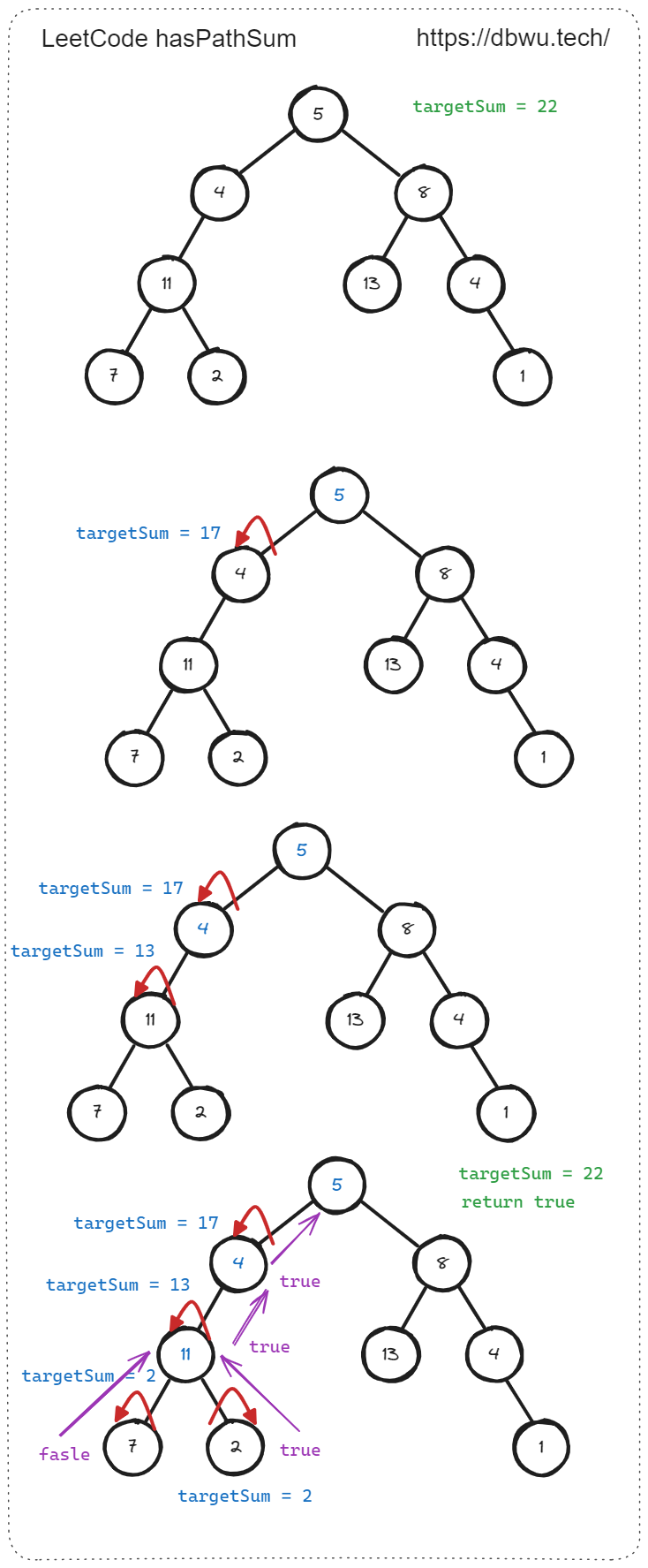
4. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
当 targetSum = 22 时返回 true, 因为 5 + 4 + 11 + 2 = 22。
解题思路:
- 识别递归边界: 如果节点为 nil, 直接返回 false, 如果左子树和右子树都为 nil, 直接判断并返回目标路径和是否等于当前节点值
- 在目标路径和基础上减去当前节点的值,得到剩余路径总和,递归计算左子树中是否存在 剩余的路径总和
- 在目标路径和基础上减去当前节点的值,得到剩余路径总和,递归计算右子树中是否存在 剩余的路径总和
- 只要左右子树中任一存在路径和,返回 true, 否则返回 false
// 题解代码
func hasPathSum(root *TreeNode, targetSum int) bool {
if root == nil {
return false
}
if root.Left == nil && root.Right == nil {
return root.Val == targetSum
}
// 递归计算左右子树中是否存在剩余路径总和
return hasPathSum(root.Left, targetSum-root.Val) || hasPathSum(root.Right, targetSum-root.Val)
}
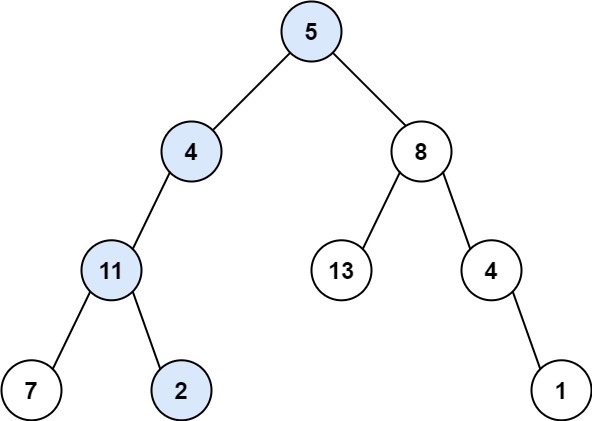
5. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
如图所示,节点 5 和节点 1 的最近公共祖先是节点 3,节点 5 和节点 4 的最近公共祖先是节点 5 (因为根据定义最近公共祖先节点可以为节点本身)。
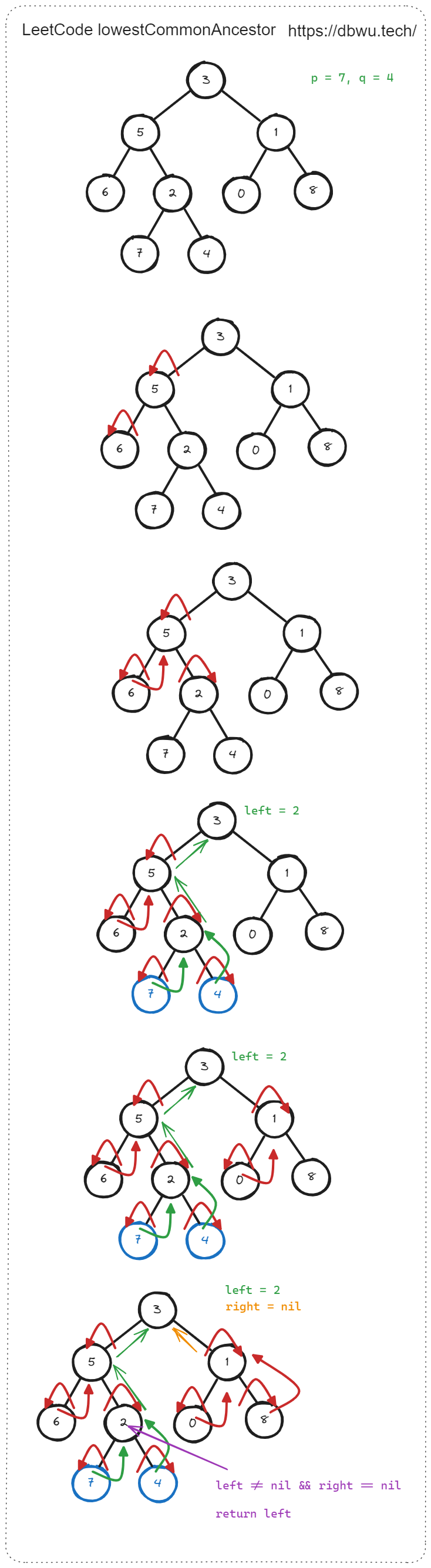
解题思路:
- 识别递归边界: 如果当前节点为 nil, 或者当前节点本身就是 p 节点或者 q 节点其中一个, 直接返回当前节点
- 递归计算左子树中 p 节点和 q 节点的公共祖先节点,记为 left
- 递归计算右子树的 p 节点和 q 节点的公共祖先节点, 记为 right
- 根据 left 和 right 的值,有可以分为 4 种情况
- 如果 left 和 right 都不等于 nil, 说明 p 节点和 q 节点分布在左子树和右子树中,那么两者的公共节点就是 root 节点
- 如果 left 不等于 nil 但是 right 等于 nil, 说明 p 节点和 q 节点都在左子树中,那么两者的公共节点就是 left 节点
- 如果 left 等于 nil 但是 right 不等于 nil, 说明 p 节点和 q 节点都在右子树中,那么两者的公共节点就是 right 节点
- 如果 left 和 right 都等于 nil, 说明 p 节点和 q 节点至少有一个节点不存在树中,那么两者的公共节点就是 right 节点,这种情况可能会出现在递归的子树中,例如 p 节点和 q 节点位于树的深层,而 root 节点位于树的浅层 (例如上图中在左子树中查找节点 1 和 8 时,
lowestCommonAncestor(5, 1, 8))
// 题解代码
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil || p == root || q == root {
return root
}
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
// 根据 left 和 right 的值,有可以分为 4 种情况
if left != nil {
if right != nil {
// 情况 1
return root
}
// 情况 2
return left
}
// 情况 3, 4
return right
}
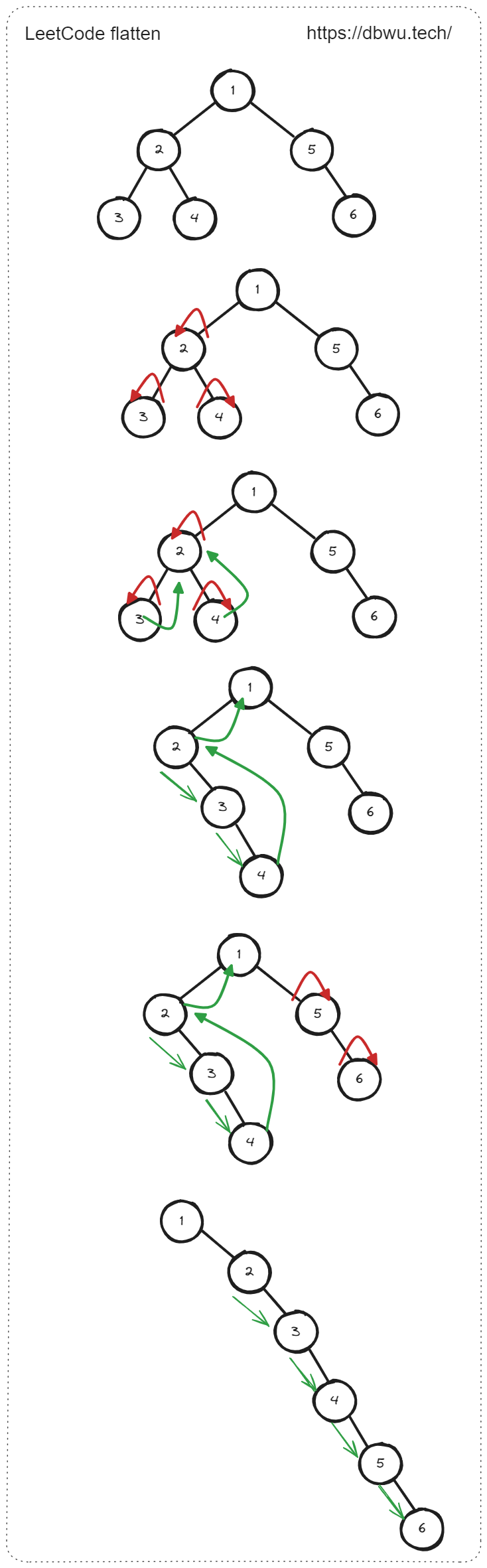
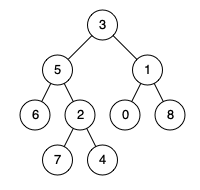
6. 二叉树展开为链表
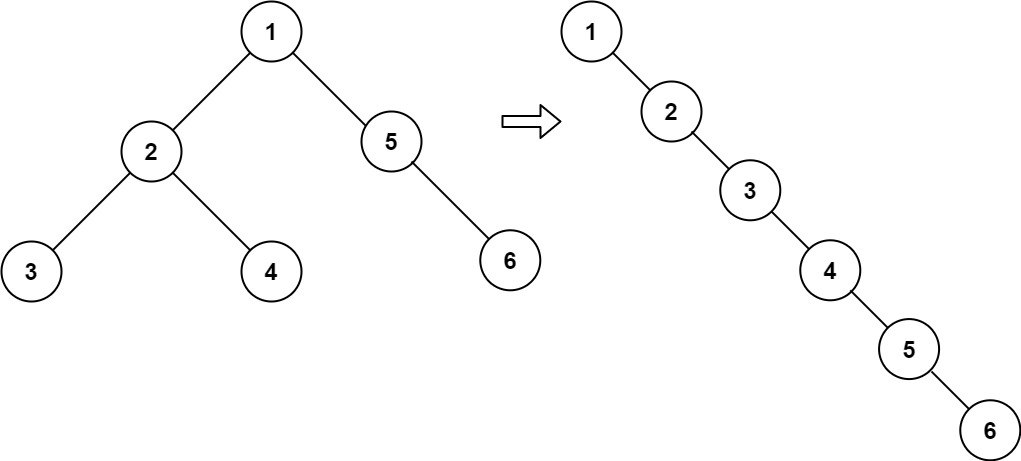
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 展开后的单链表应该与二叉树 先序遍历 顺序相同。
下面是一个二叉树展开为链表的示例。
解题思路:
- 识别递归边界: 如果节点为 nil, 直接返回
- 将右子树 (递归) 展开成链表
- 将左子树 (递归) 展开成链表
- 在单个递归过程中,将当前 root 节点进行展开:
- 将 root 节点的 Right 节点暂存起来 (tmp 节点)
- 将 root 节点的 Right 设置为 Left 节点
- 将 root 节点的 Left 节点设置为 nil
- 将现在的 Right 节点 (原来的 Left 节点) 连接到 原来的 Right 节点 (tmp 节点)
// 题解代码
func flatten(root *TreeNode) {
if root == nil {
return
}
flatten(root.Left)
flatten(root.Right)
tmp := root.Right
root.Right = root.Left
root.Left = nil
for root.Right != nil {
root = root.Right
}
root.Right = tmp
}