LeetCode 位运算刷题模板
概述
打开 LeetCode 官网,根据标签筛选题目,可以看到 “位运算” 相关的题目一共有 226 道题,如果我们逐个题目全部刷完,要投入相当可观的时间精力, 而且因为位运算类型题目并不是高频考题,所以更聪明的方式是掌握核心考点,了解常考题目,以最小的时间投入换取更大的刷题效率回报。
当面试中出现 “位运算” 相关题目时,大部分情况下,主考官的考点绝对不是使用位运算来实现各种奇技淫巧,而是考察求职者对于位运算的基础掌握情况, 也就是常见的 AND, OR, XOR, Complement, 位移 操作,确认了刷题目标,我们就可以将刷题策略 (方法) 简化为三步:
- 熟练掌握常用位运算 (夯实基础)
- 筛选出 LeetCode 中和 “位运算” 相关的高频考题,分析每个题的核心考点 (触类旁通)
- 提炼核心考点并根据题目进行分类,深入理解并掌握每种题型并形成模板,理想情况下,看到题目时,可以快速进行分类并套用对应的模板解题 (举一反三)
笔者经验
笔者只刷过简单和中等难度的 “位运算” 题目,其中 70% 简单题,30% 的中等题,代码基本都在 10 行以内,对于困难级别的题目,虽然标签中有 “位运算”, 但是如果使用位运算来解题的话,代码复杂度会很高,因为这类题目的考点并非 “位运算”,而是其他方面的知识点考察,例如贪心、回溯、DFS 等,只是恰好可以使用 “位运算” 来解题。
如果读者时间精力有限的话,针对这类困难的 “位运算” 相关题目,不建议研究位运算的解法,而是应该尝试从其他方向解题。
此外,如上文中提到的,真正的面试中,“位运算” 并非高频考题,所以笔者认为正确的或者说更有价值的选择应该是时间投入到更高频的题目上,例如二叉树类、链表类、排序类题目。 下面笔者就自己的刷题经验,做一个简单的分享。
统计位 1 的个数
几乎 30% “位运算” 相关的题都是此题的衍生题,所以这里直接提炼出一个通用解题模板,遇到类似题目时,直接套模板即可。
原题
191 题. 位 1 的个数
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'
输入:n = 00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'
模板
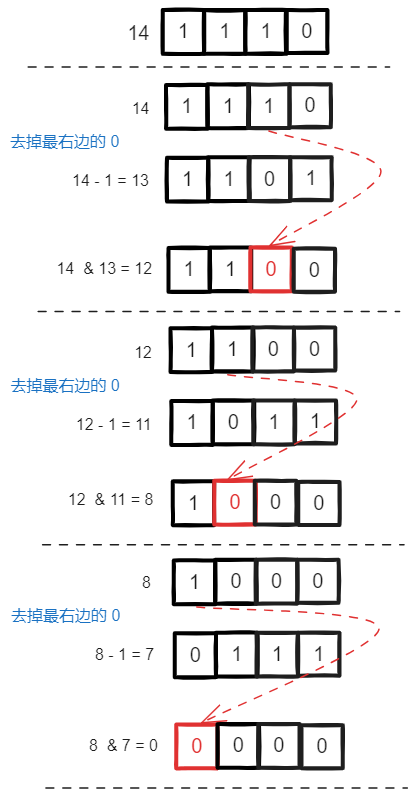
下面的方法可以计算出一个数字的二进制表示中位为 1 的个数。
func onesCount(num uint32) int {
// 累计器初始值设置为 0
cnt := 0
for num != 0 {
// 每次去掉二进制表示中最右边的 1
// 过程可以参考上面的示例图
num &= num - 1
// 增加累计结果
cnt++
}
// 返回累计结果
return cnt
}
衍生题目
有了上面的模板之后,我们在遇到相关衍生题目时,就可以直接套用模板,然后快速解题。
338 题. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
解题思路: 也就是计算从 0 到 n 之间,每个数字中的位为 1 的个数,直接套用模板加循环即可。
// 伪代码实现
func countBits(num int) []int {
res: = make([]int,num+1)
for i := 0; i <= num; i++{
// 逐个计算数字的二进制表示中 1 的个数
res[i] = onesCount(i)
}
return res
}
762 题. 二进制表示中质数个计算置位
给你两个整数 left 和 right ,在闭区间 [left, right] 范围内,统计并返回 计算置位位数为质数 的整数个数。
解题思路:和刚才的题目类似,只是多加了一层判断是否为质数的处理逻辑,直接套用模板加循环即可。
// 伪代码实现
func countPrimeSetBits(left int, right int) int {
var res int
for ; left <= right; left++ {
if isPrime(onesCount(uint32(left))) {
res++
}
}
return res
}
// 判断一个数字是否为质数
func isPrime(x int) bool {
...
}
0506 题. 整数转换
整数转换。编写一个函数,确定需要改变几个位才能将整数 A 转成整数 B 。
解题思路:A 需要转换多少位才可以变为 B, 换个角度也就是计算 A 和 B 的异或结果中,有多少位为 1 的个数,依然直接套用模板即可。
// 伪代码实现
func convertInteger(A int, B int) int {
return onesCount( uint32( A ^ B) )
}
2220 题. 转换数字的最少位翻转次数
给你两个整数 start 和 goal ,请你返回将 start 转变成 goal 的 最少位翻转 次数,虽然换了名称和描述,但是上面的题本质就是一个题。
出现 N 次的数字
这是一个非常经典的 “位运算” 问题,虽然使用哈希和桶方案可以简单快速解决,但是此类题目一般会有空间复杂度要求,如果在面试中遇到此类题目,那么考点百分百是位运算。
原题
137 题. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现三次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
模板
想要从位运算的角度来解题,我们首先来分析一下给定不同参数的情况下,每个参数的二进制表示形式,然后尝试从中找到一些规律。
示例 1:
输入:nums = [2, 2, 3, 2]
输出:3
将参数分别转换为二进制表示形式:
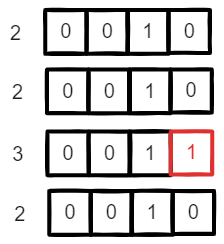
通过上图可以看到,只出现一次的数字 3 包含 2 个二进制位为 1,其中只有一个位和其他三个数字不同,根据这个规律,可以将参数数组中的所有元素逐个计算每个二进制为 1 的个数 (Sum 操作),并对 3 进行取模 (Mod 操作),得到如下结果:
因为除了只出现一次的数字,其他数字全部出现了三次,其中每个二进制位只会有两种结果: 0 或者 1:
- 0 表示只出现 1 次的数字,该二进制位为 0
- 1 表示只出现 1 次的数字,该二进制位为 1
那么最终计算出来每个二进制位上面的数字,转换为十进制数字之后,也就是题目的答案:只出现了一次的数字。
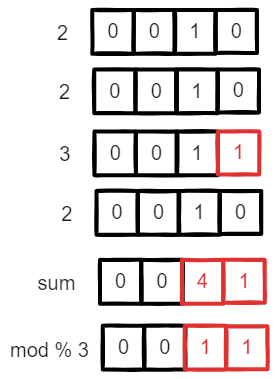
通过上图可以看到,最终的二进制表示就是题目的答案。
那么如何实现上面的 “逐个计算并保存” 转化为具体的代码呢?一个直观的方法使用一个数组存储表示所有元素每个二进制位取模 3 之后的结,但是这样实现有两个弊端:
- 浪费空间,如果结果是 64 bit 的数字,那么就需要长度为 64 的数组用于存储每个二进制位的值
- 计算复杂,需要先将每个二进制位的值 (0|1) 存入数组对应的位置,然后在将数组中所有元素整个转换为一个具体的十进制数字。
但是其实有一个时间和空间都更加高效的方案: 位运算中的位移,我们只需要声明一个结果变量,然后在计算出每个二进制位时,设置该结果变量对应的二进制位值即可。
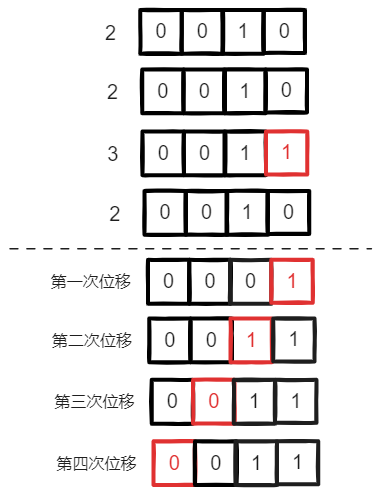
下面是对应的伪代码实现。
func singleNumber(nums []int) int {
// 除了结果数字外,其他数字出现的次数
cnt := 3
// 只需要声明一个变量作为结果返回值
res := int32(0)
// 这里以 32 位数字为例
// 如果是 64 位数字,直接换成 64 即可
for i := 0; i < 32; i++ {
var sum int32
// 逐个计算数组中所有元素当前二进制位为 1 的个数
for _, num := range nums {
sum += int32(num) >> i & 1
}
// 使用二进制位为 1 的个数取模其他数字出现的次数
// 然后左移改变结果 (答案) 数字对应的二进制位
res |= (sum % cnt) << i
}
return int(res)
}
衍生题目
模板:给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现 M 次。找出那个只出现了一次的元素。
通用代码 (只需要将 cnt 改为其他元素出现的次数即可):
func singleNumber(nums []int) int {
// 除了结果数字外,其他数字出现的次数
cnt := 3
// 例如其他元素出现了 4 次
// cnt := 4
// 例如其他元素出现了 5 次
// cnt := 5
// 例如其他元素出现了 6 次
// cnt := 6
// 只需要声明一个变量作为结果返回值
res := int32(0)
// 这里以 32 位数字为例
// 如果是 64 位数字,直接换成 64 即可
for i := 0; i < 32; i++ {
var sum int32
// 逐个计算数组中所有元素当前二进制位为 1 的个数
for _, num := range nums {
sum += int32(num) >> i & 1
}
// 使用二进制位为 1 的个数取模其他数字出现的次数
// 然后左移改变结果 (答案) 数字对应的二进制位
res |= (sum % cnt) << i
}
return int(res)
}
477 题. 汉明距离总和
给你一个整数数组 nums,请你计算并返回 nums 中任意两个数之间 汉明距离的总和 。
解题思路:类似上面的解题方案,分别计算出数组中所有元素在不同二进制位上面的差异总值,最后累加即可。
清除最右侧为 1 的位
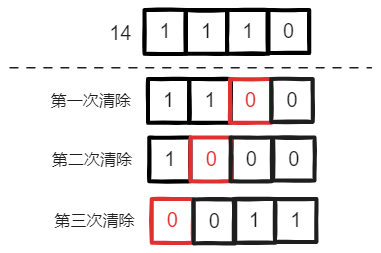
单次清除转为代码为:
println(14 & (14-1))
模板
如果需要清除数字中全部的 1 (也就是变为 0),需要的次数:
func numberOfSteps(num int) int {
var res int
for num != 0 {
num &= num - 1
res++
}
return res
}
衍生题目
1342 题. 将数字变成 0 的操作次数
解题思路: 直接套用模板即可。
201 题. 数字范围按位与
给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。
解题思路: 遍历参数范围区间,每次取代最大数字最右边为 1 的位,直接套用模板即可。
func rangeBitwiseAnd(left int, right int) int {
for left < right {
right &= right-1
}
return right
}
231 题. 2 的幂
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。
解题思路:
- 先看看 2 的幂的数字,都有什么特征?
- 2 = 0010
- 4 = 0100
- 8 = 1000
- 16 = 0001 0000
- 特征就是每个数字的二进制表示中,只有 1 个二进制位的值为 1
- 不管这个二进制位在多少位,都可以视为最右边,所以只需要将数字最右边位为 1 去掉,然后判断其是否等于 0 即可,如果等于 2 就必然是 2 的幂次
func isPowerOfTwo(n int) bool {
return n > 0 && n & (n-1) == 0
}
其他操作
- 设置第 k 位:
s |= (1 << k) - 第 k 位置 0:
s &= ~(1 << k) - 切换第 k 位值:
s ^= ~(1 << k) - 取出最小非 0 位:
s & (-s) - 保留最右边的 1:
bit := xor & -xor - 取出最小 0 位:
~s & (s + 1)
