LeetCode DFS 刷题模板
📖 概述
DFS (深度优先搜索) 是一种用于遍历树或图数据结构的算法,其基本思想是从起始节点 (通常是根节点) 出发,沿着路径尽可能进行深度搜索,直到到达最深的节点,然后再回溯到之前的节点继续 (递归) 深度搜索其他路径,直到搜索完所有可能的路径,算法结束。
DFS: 不撞南墙不回头
BFS: 步步为营
算法基本步骤
- 从起始节点 (根节点) 开始遍历,将其标记为已访问
- 单次遍历过程中,对于 “当前节点”,依次访问其所有相邻节点
- 对于每个相邻节点,如果未被访问过,递归调用 DFS
- 当所有相邻节点都被访问过或当前节点没有相邻节点时,回溯到上一级节点,继续搜索其他路径
执行过程示例
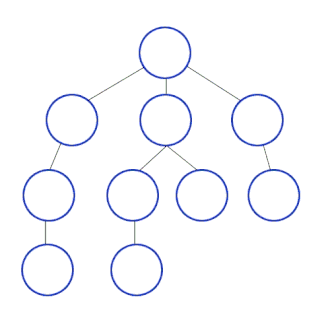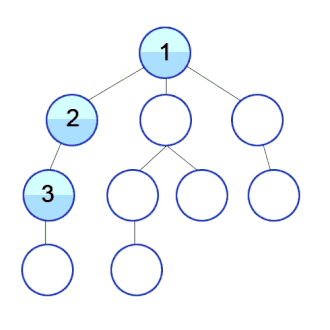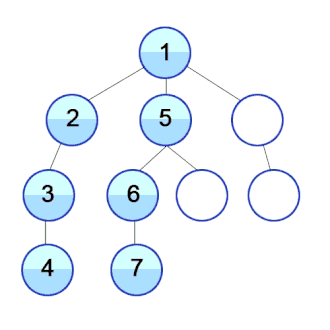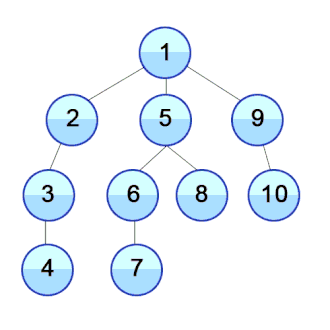
下面是一个典型的图数据结构:
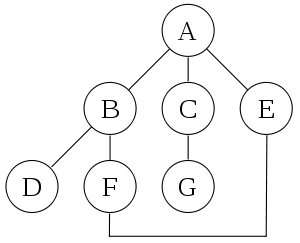
对该图执行 DFS 算法时,具体的执行过程中,每个节点被访问的顺序如图所示:
伪代码
下面的是对应的 Golang 伪代码:
// 使用邻接表 表示图的数据结构
type Graph struct {
vertices map[int][]int
}
// 深度优先搜索
func DFS(graph Graph, start int, visited map[int]bool) {
// 标记当前节点为已访问
visited[start] = true
// 遍历当前节点的所有相邻节点
for _, v := range graph.vertices[start] {
// 如果相邻节点未被访问过,递归调用 DFS
if !visited[v] {
DFS(graph, v, visited)
}
}
}
// 从节点 0 开始进行深度优先搜索
DFS(graph, 0, visited)
💡 典型题目 (图)
LeetCode 中的 DFS (图数据结构) 相关题目都是在 DFS 基础上加上题目的具体逻辑即可,解题步骤 (模板) 可以分为四步:
- 确定 DFS 结束条件和边界处理 (核心)
- 确定 DFS 起始节点
- 确定单次访问节点
- DFS 过程中的状态变量如何更新 (一般使用参数传递)
// DFS 刷题模板代码 (针对图数据结构)
func Solution(...) ... {
// 初始化状态
...
// 定义 DFS 函数
var dfs func(...)
// 实现 DFS 函数
dfs = func(...) {
// 递归结束条件 (边界处理)
if ... {
return
}
// 状态更新
...
// 遍历当前节点的相邻节点或下一步可能的选择
for ... {
// 如果符合题目逻辑条件,继续递归
// 如果下一步有效,进行递归调用
if ... {
dfs(...)
}
}
}
// 返回调用 DFS 函数的结果
return ...
}
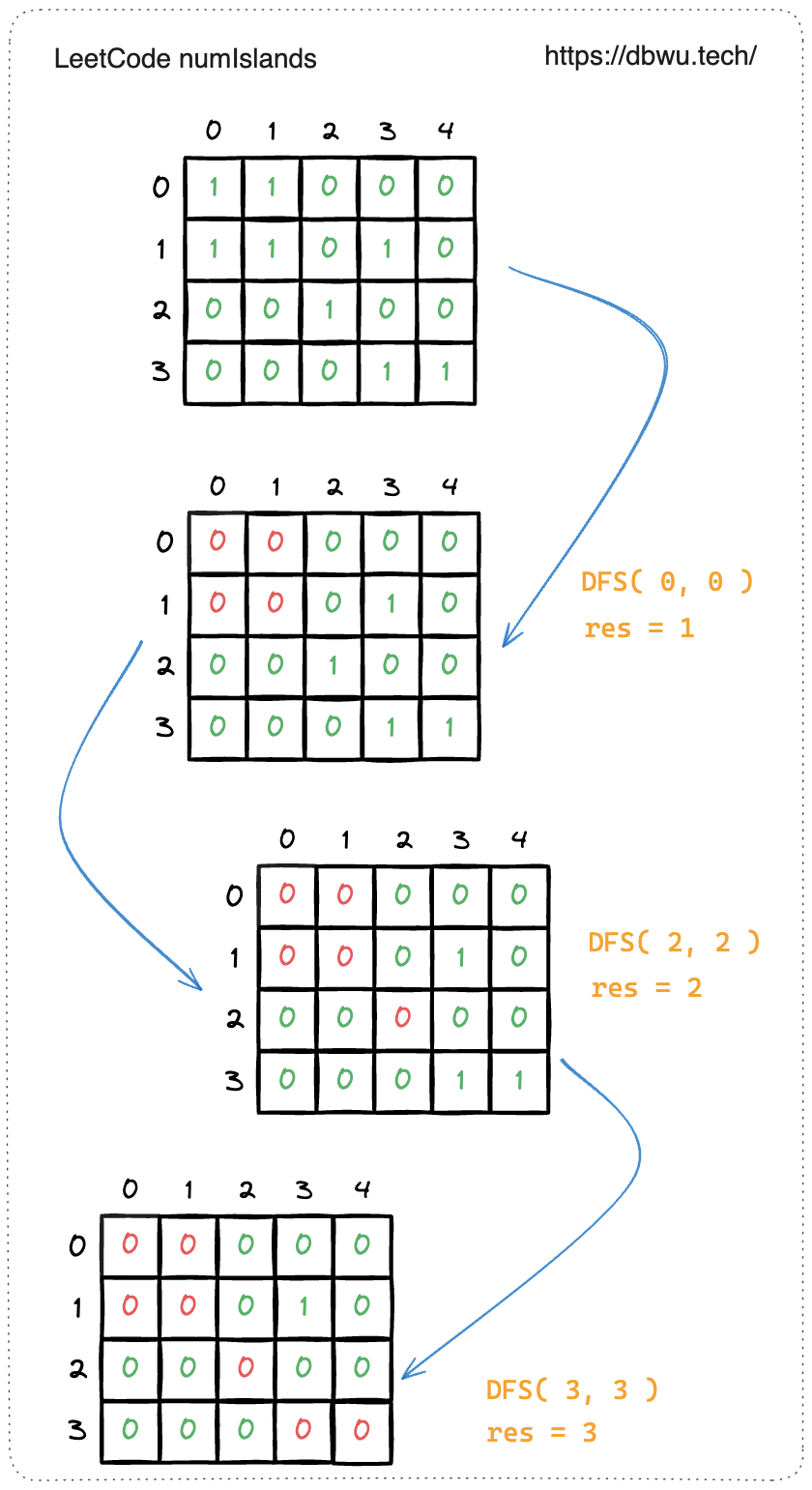
1. 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
# 示例来自: https://leetcode.cn/
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
快速套模板:
- 递归结束条件: 当前坐标超出边界 (二维数组索引越界),或者当前节点不是 ‘1’ (陆地)
- 确定 DFS 起始节点: 参数使用二维数组表示图的邻接表,那么就从数组第一个元素开始
grid [0][0] - 确定单次访问节点: 当前节点 上下左右 4 个方向所有为 ‘1’ (陆地) 的节点 (这样就可以连成一片,形成一个小岛),然后递归,单个节点访问之后,将值标记为 ‘0’, 避免重复访问
- 状态变量如何更新: 以当前节点开始,完成一轮 DFS 过程,岛屿数量 + 1
// 题解代码
func numIslands(grid [][]byte) int {
res := 0
for row := range grid {
for col := range grid[row] {
if grid[row][col] == '1' {
// 如果找到一块陆地,以该坐标为中心,上下左右四个方向继续探索
res++
dfs(grid, row, col)
// 递归完成之后,以当前坐标为中心的陆地全部被标记为 '0'
}
}
}
return res
}
func dfs(grid [][]byte, row, col int) {
// 递归结束条件 (边界处理)
// 如果坐标已越界或者当前坐标不是陆地
// 直接返回
if row < 0 || row >= len(grid) || col < 0 || col >= len(grid[0]) || grid[row][col] == '0' {
return
}
// 已经探索过的坐标标记为 0, 避免重复计算
grid[row][col] = '0'
dfs(grid, row-1, col) // ⬆ 方向递归
dfs(grid, row+1, col) // ⬇ 方向递归
dfs(grid, row, col-1) // <- 方向递归
dfs(grid, row, col+1) // -> 方向递归
}
2. 被围绕的区域
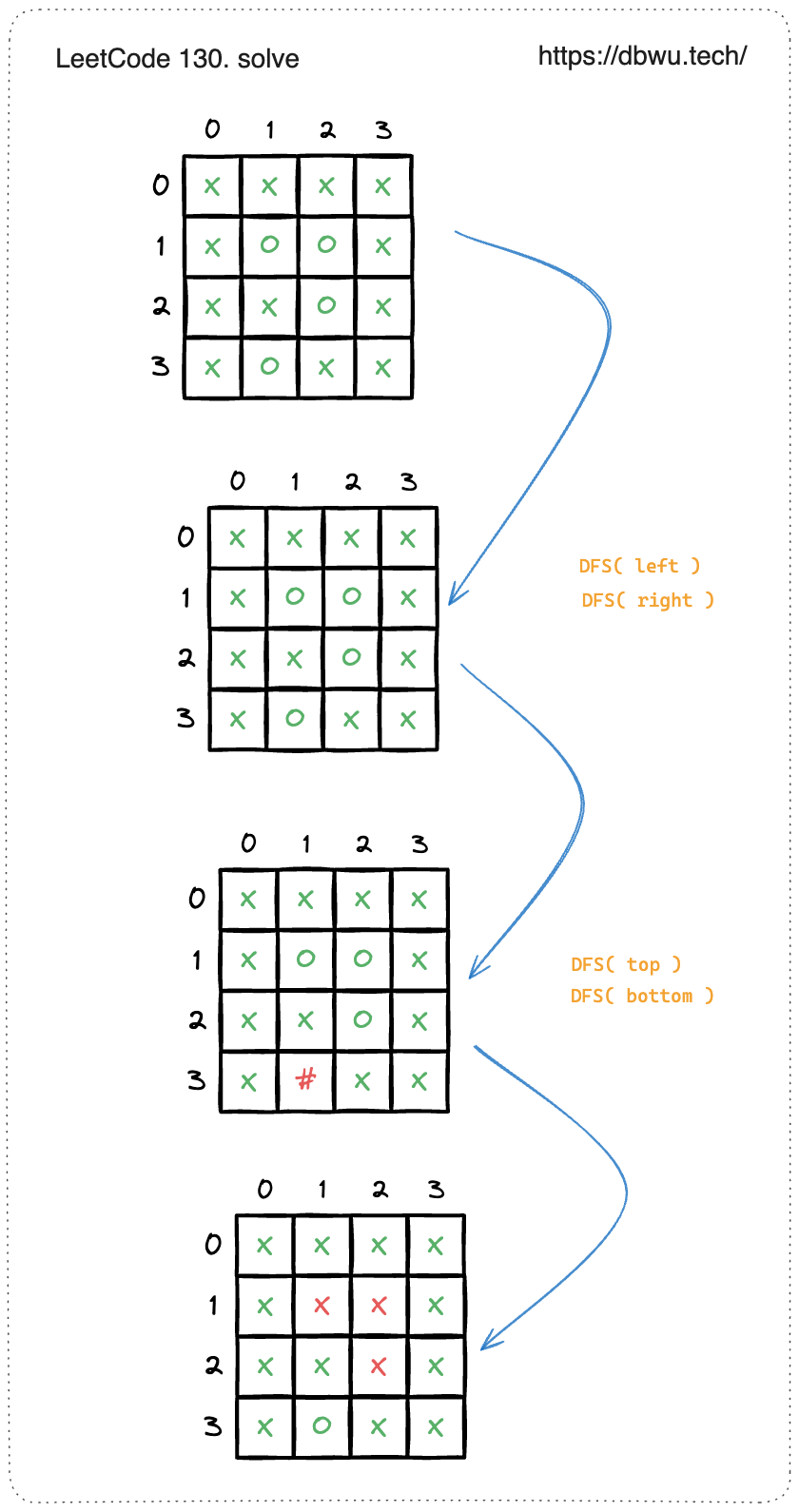
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
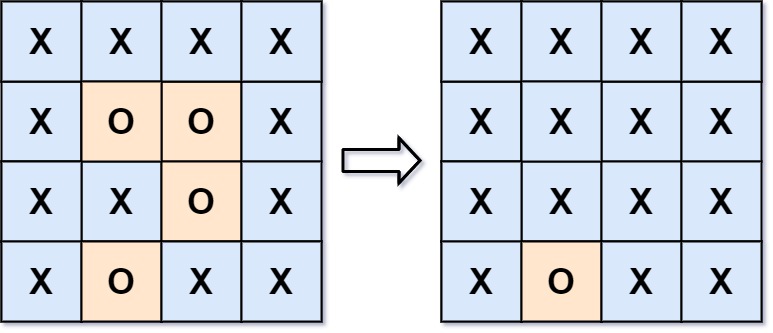
解题思路:
题目解释中提到:任何边界上的 O 都不会被填充为 X, 所有的不被包围的 O 都直接或间接与边界上的 O 相连。那么只需要将所有可以连通的进行标记,剩下的就是无法连通的。
题目要求四个边界上面的格子 ‘O’ 不需要被更新,那么如何在 DFS 的递归执行过程中规避掉这个问题呢?我们可以使用一个额外的字符 # 作为临时字符来替换掉边界上的 ‘O’, 专门用于标记已经更新过的格子,最后再将临时字符 # 的格子替换为 ‘O’。
快速套模板:
- 递归结束条件: 当前坐标超出边界 (二维数组索引越界),或者当前节点不是 ‘O’
- 确定 DFS 起始节点: 参数使用二维数组表示图的邻接表,那么就从数组第一个元素开始
board [0][0] - 确定单次访问节点: 将上下左右 四个边界的格子 及其 相连的格子 标记为 “已连通“,使用字符
# - 状态变量如何更新: 本题只涉及到数据修改,没有返回值,所以不需要状态变量
// 题解代码
func solve(board [][]byte) {
// 边界条件判断
rows := len(board)
if rows == 0 {
return
}
cols := len(board[0])
if cols == 0 {
return
}
// 边界上的格子 'O' 预处理
// 将左右边界进行标记为 "已连通"
for row := 0; row < rows; row++ {
dfs(board, row, 0)
dfs(board, row, cols-1)
}
// 将上下边界进行标记为 "已连通"
for col := 1; col < cols - 1; col++ {
dfs(board, 0, col)
dfs(board, rows-1, col)
}
// 现在从矩阵的最外侧作为出发点
// 上下左右四个方向已经连通
// 只需要遍历一次矩阵
// 将 # 修改为 0, 因为这些属于边界上的 0
// 将 0 改为为 X, 因为这些不属于边界上的 0
for row := 0; row < rows; row++ {
for col := 0; col < cols; col++ {
if board[row][col] == '#' {
board[row][col] = 'O'
} else if board[row][col] == 'O' {
board[row][col] = 'X'
}
}
}
}
func dfs(board [][]byte, row, col int) {
// 递归结束条件 (边界处理)
if row < 0 || row >= len(board) || col < 0 || col >= len(board[0]) || board[row][col] != 'O' {
return
}
board[row][col] = '#'
dfs(board, row-1, col) // ⬆ 方向递归
dfs(board, row+1, col) // ⬇ 方向递归
dfs(board, row, col-1) // <- 方向递归
dfs(board, row, col+1) // -> 方向递归
}
3. 克隆图
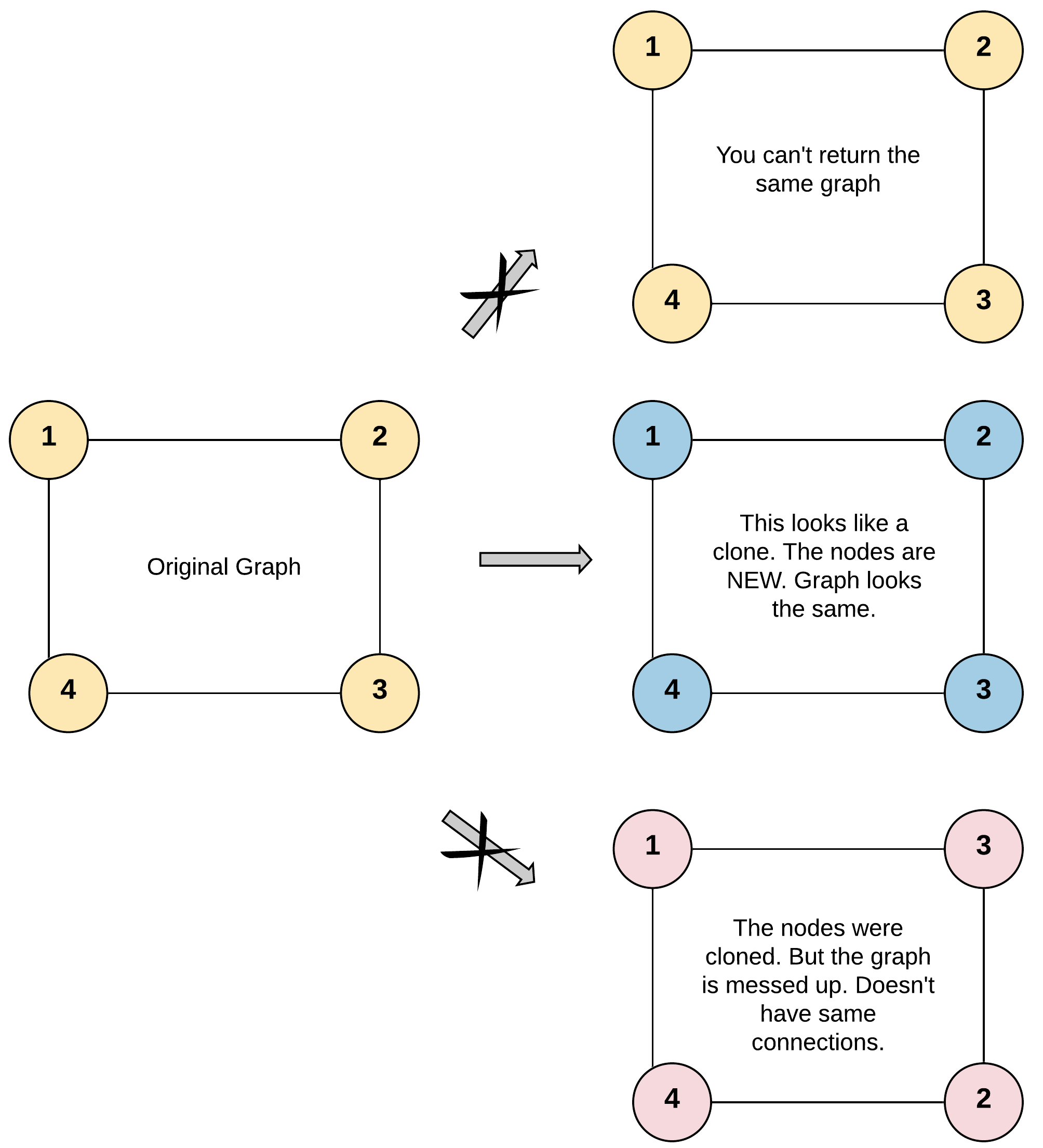
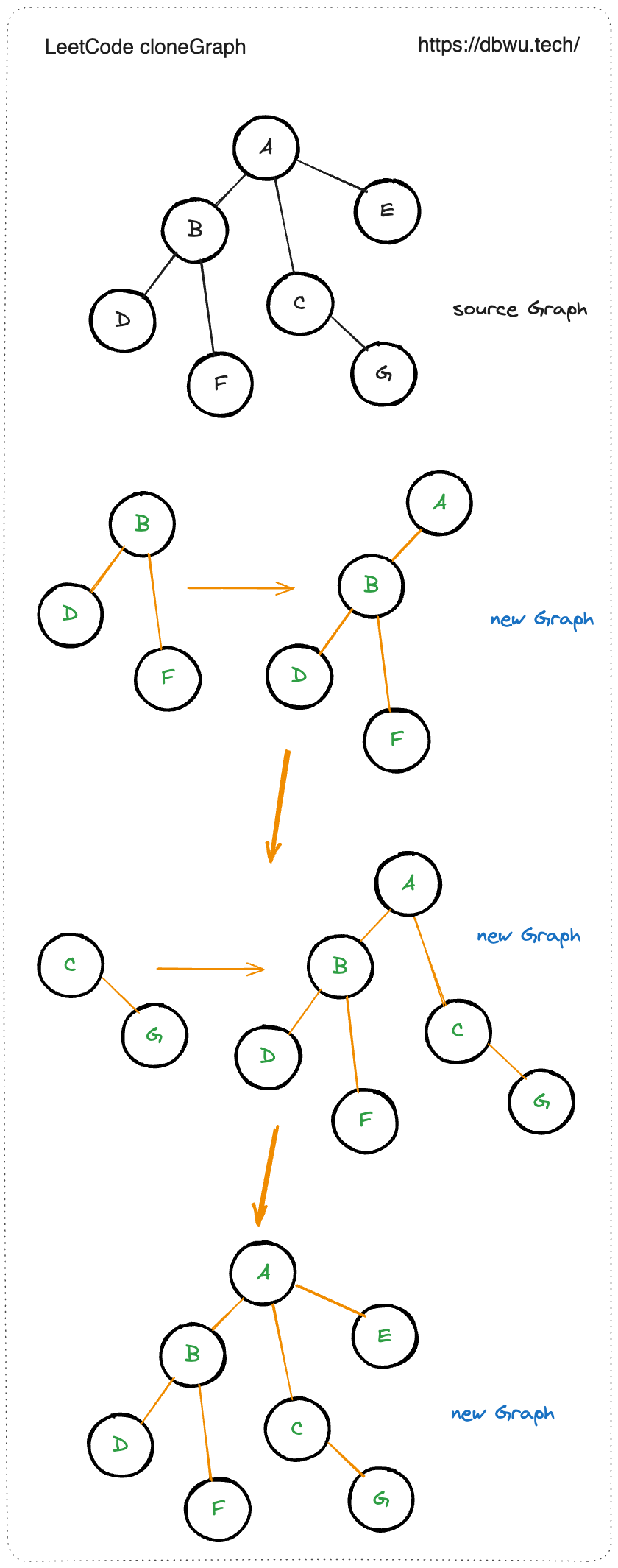
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
节点的深度拷贝需要满足两个条件:
- 新节点必须和源节点的值一样,并且拥有新的内存地址空间和数据结构
- 各个新节点之间的关系必须和源节点之间的关系一致
快速套模板:
- 递归结束条件: 当前节点为 nil, 或者当前节点已经被克隆,直接返回已经克隆的新节点
- 确定 DFS 起始节点: 题目给出的参数节点
- 确定单次访问节点: 当前节点的所有邻居节点
- 状态变量如何更新: 使用一个 Hash 存储源和克隆的新节点之间的关系,访问当前源节点时,将克隆后的新节点和源节点完成映射
// 题解代码
func cloneGraph(node *Node) *Node {
// 以参数节点开始进行 DFS 遍历
// 使用参数传递源节点和新节点的 Hash Map
return dfs(node, make(map[*Node]*Node))
}
func dfs(node *Node, visited map[*Node]*Node) *Node {
// 递归结束条件 (边界处理)
if node == nil {
return node
}
// 如果当前节点已经被克隆过,直接返回克隆后的新节点
if _, ok := visited[node]; ok {
return visited[node]
}
// 克隆当前节点
cloneNode := &Node{node.Val, []*Node{}}
// 将当前节点标记为已经克隆
visited[node] = cloneNode
// 遍历当前的节点的邻节点,递归克隆
for _, v := range node.Neighbors {
cloneNode.Neighbors = append(cloneNode.Neighbors, dfs(v, visited))
}
return cloneNode
}
💡 DFS 和二叉树
使用 DFS 解决二叉树 (数据结构) 相关问题时,因为左右子树需要分别进行递归操作,这是就无法计算一些 “中间状态数据值”,例如每层的节点数量、每层的节点值平均值,针对这类问题,可以将中间状态数据值保存到全局状态存储中,在 DFS 过程结束之后再计算。
由于 “中间状态数据值” 需要在递归的过程中不断被更新,所以调用时 需要传入指针变量,“中间状态数据值” 使用语义非常清晰,降低了代码阅读难度。
刷题模板
LeetCode 中的二叉树 DFS 相关题目都是在 DFS 算法基础上加上具体逻辑即可,和图 (数据结构) 不同的地方在于: 二叉树的每个节点会有左右两个子节点, 解题步骤 (模板) 可以分为四步:
- 确定 DFS 结束条件和边界处理 (核心), 一般是
if root == nil { return } - 确定 DFS 起始节点,一般是二叉树
root根节点 - 确定单次访问节点,也就是当前节点的左右节点
root.Left,root.Right - DFS 过程中的状态变量如何更新 (一般使用参数传递,例如当前所在树的层级、题目要求的逻辑数据等)
下面是一个使用 DFS 遍历的代码模板:
// DFS 刷题模板代码 (针对树数据结构)
func levelOrderDFS(root *TreeNode) {
// 指针传递,充当 “全局变量”
// 用于处理和存储 “中间状态数据值”
var res []int
// 层级从 0 开始
dfs(root, 0, &res)
return res
}
// 注意 res 的形参类型
func dfs(root *TreeNode, depth int, res *[]int) {
// DFS 递归条件处理
if root == nil {
return
}
// 根据具体的逻辑执行某些初始化操作
if depth == len(*res) {
...
}
// 根据具体的逻辑,更新全局变量数据
...
// 递归左子树 层级 + 1
dfs(root.Left, depth+1, res)
// 递归右子树 层级 + 1
dfs(root.Right, depth+1, res)
}
通用递归边界条件检测
对于树数据结构来说,正确处理 DFS 递归条件除了避免代码执行陷入死循环之外,还可以 及时剪枝,提升代码执行效率、代码可读性。
下面列举了几个常见的边界条件检测:
// 最常见的树递归边界处理
if root == nil {
return }
// 比较树的两个子节点是否相同
if p == nil && q == nil {
return true
}
if p == nil || q == nil {
return false
}
if p.Val != q.Val {
return false
}
💡 典型题目 (二叉树)
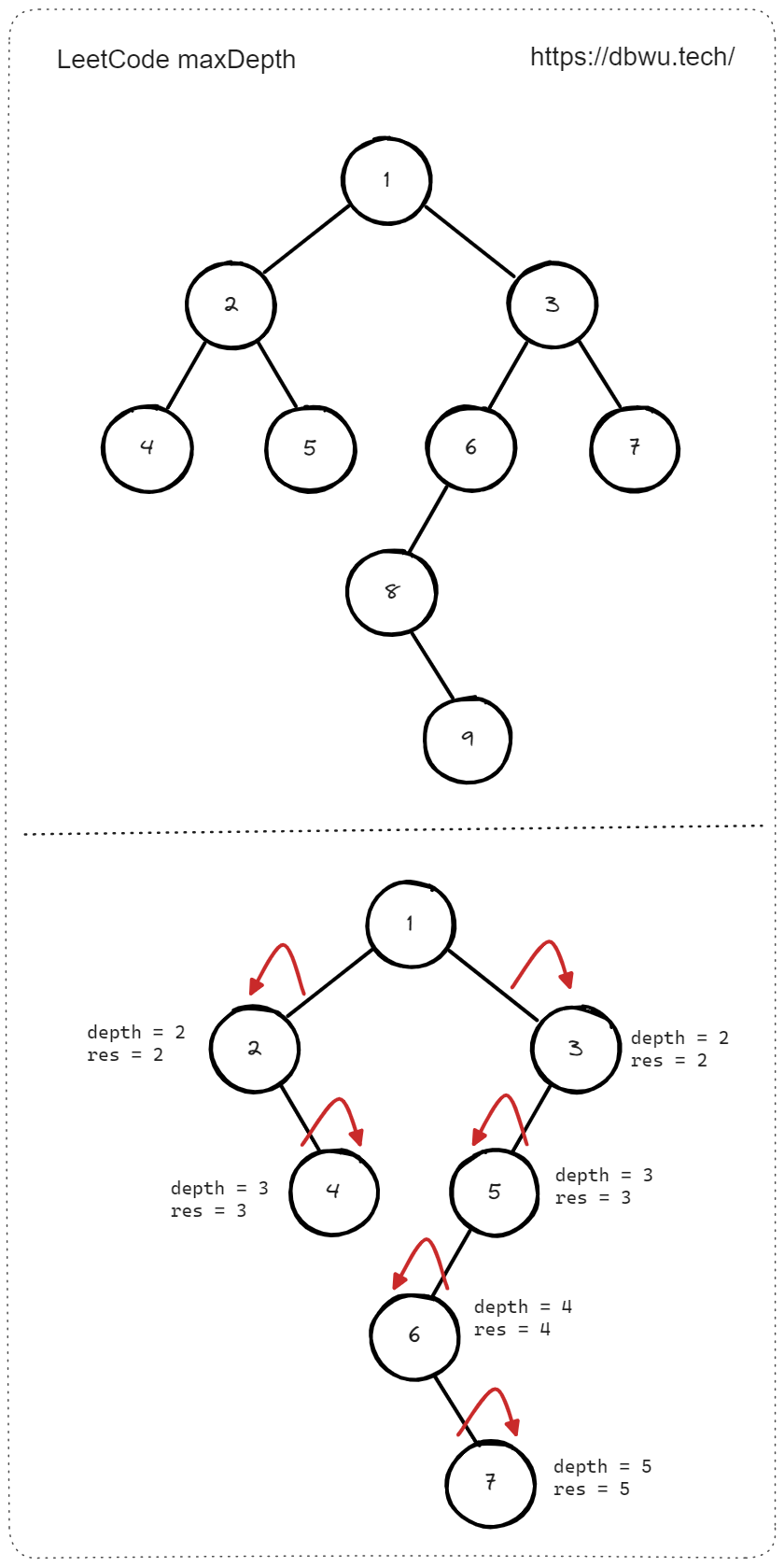
1. 二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
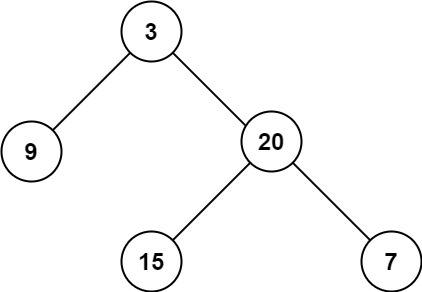
如图所示的 树 的深度为 3。
快速套模板:
- 确定 DFS 结束条件和边界处理 (核心),
if root == nil { return } - 确定 DFS 起始节点,也就是参数
root根节点 - 确定单次访问节点,当前节点的左右节点
root.Left,root.Right - DFS 过程中的状态变量如何更新: (递归时使用指针类型参数传递返回值,额外传递一个参数用于表示当前树的 “层级”,也就是深度)
// 题解代码
func maxDepth(root *TreeNode) int {
// 状态变量
var res int
// 从 root 节点作为 DFS 起始节点
// 使用指针传递状态变量
dfs(root, 0, &res)
// 返回状态变量
return res
}
func dfs(root *TreeNode, depth int, res *int) {
// DFS 递归条件处理
if root == nil {
return
}
// 因为存在树的两边高度不相等的情况
// 所以最大深度以 [当前深度] 和 [已知的最大深度] 中的较大值为准
*res = max(*res, depth+1)
// 递归左子树时,深度 + 1
dfs(root.Left, depth+1, res)
// 递归右子树时,深度 + 1
dfs(root.Right, depth+1, res)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
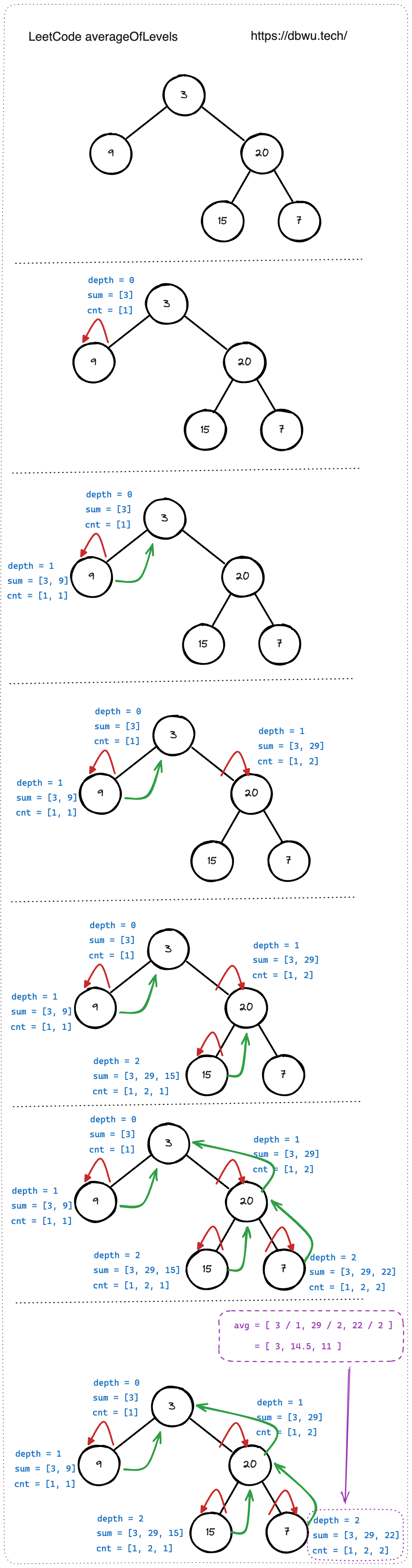
2. 二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。
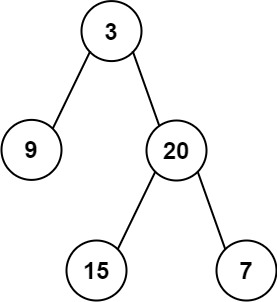
给出上图所示的二叉树,会输出如下答案:
输出:[3.00000,14.50000,11.00000]
解释:第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
快速套模板:
- 确定 DFS 结束条件和边界处理 (核心),
if root == nil { return } - 确定 DFS 起始节点,也就是参数
root根节点 - 确定单次访问节点,当前节点的左右节点
root.Left,root.Right - DFS 过程中的状态变量如何更新: 使用指针数组参数传递 “每层节点累加值” 和 “每层节点数量”,单个递归过程中,将每层的 “累加值“ 和 “节点数量” 保存起来,然后递归调用左右子树即可,最后 DFS 结束之后根据 “每层节点累加值” 和 “每层节点数量” 计算平均值
// 题解代码
func averageOfLevels(root *TreeNode) []float64 {
// sum 存储每层节点累加值
// cnt 存储每层节点数量
var sum, cnt []int
// 从 root 节点作为 DFS 起始节点
// 使用指针传递状态变量
dfs(root, 0, &sum, &cnt)
// 计算每层的平均值
var res []float64
for i := range sum {
res = append(res, float64(sum[i])/float64(cnt[i]))
}
return res
}
func dfs(root *TreeNode, depth int, sum, cnt *[]int) {
// DFS 递归条件处理
if root == nil {
return
}
// 遇到每个层级的第一个节点时,初始化累加器和计数器
if depth == len(*sum) {
*sum = append(*sum, root.Val)
*cnt = append(*cnt, 1)
} else {
// 遇到了每个层级的第 2 - N 个节点
// 其中 N 等于该层上面的节点数量
// 对于树的每一层,这个分支会执行 N - 1 次
(*sum)[depth] += root.Val
(*cnt)[depth]++
}
// 递归左子树时,深度 + 1, 同时传递两个指针数组
dfs(root.Left, depth+1, sum, cnt)
// 递归右子树时,深度 + 1, 同时传递两个指针数组
dfs(root.Right, depth+1, sum, cnt)
}
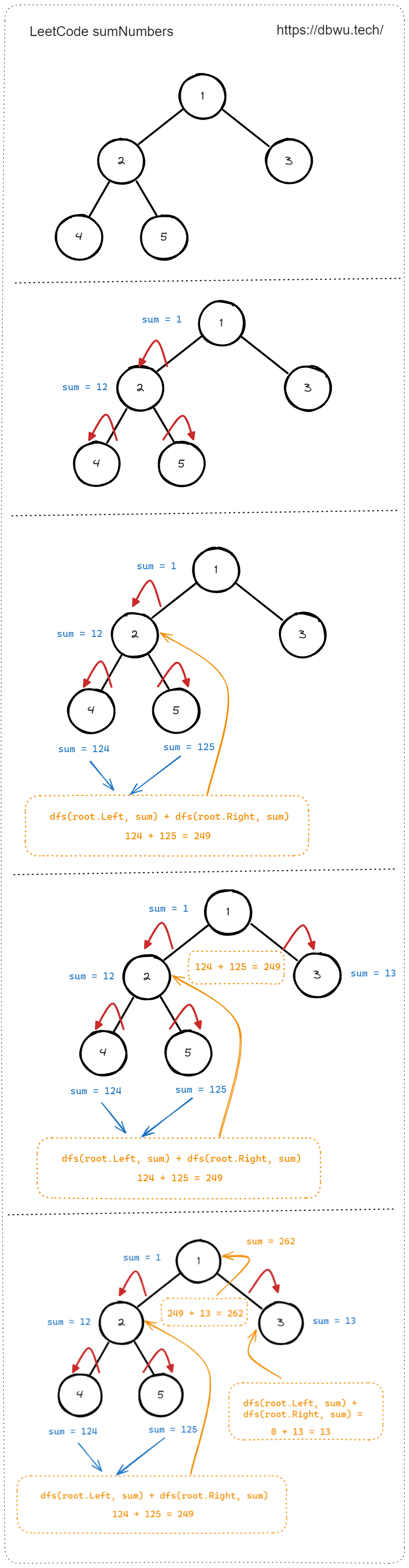
3. 二叉树根节点到叶节点数字之和
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字: 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。 叶节点 是指没有子节点的节点。
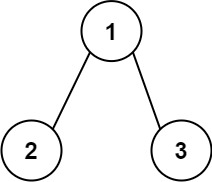
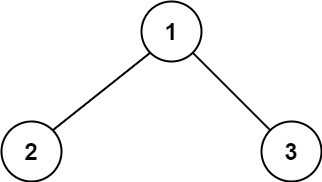
# 如图所示
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
二叉树的遍历过程中,除了使用指针变量作为 “中间状态数据值” 之外,也可以使用返回值的方式实现,不论哪种方式,最重要的是处理好 “中间状态数据值” 在递归过程中的更新。
快速套模板:
- 确定 DFS 结束条件和边界处理 (核心), 这道题存在两个边界条件:
- 如果当前节点为 nil, 直接返回 0,
if root == nil { return 0 } - 如果当前节点的左右子节点都为 nil, 说明当前节点就是叶子节点,直接返回 “当前累加值”
- 如果当前节点为 nil, 直接返回 0,
- 确定 DFS 起始节点,也就是参数
root根节点 - 确定单次访问节点,当前节点的左右节点
root.Left,root.Right - DFS 过程中的状态变量如何更新: 使用参数传递 “当前累加值”,单个递归过程中,使用当前节点值计算并更新 “当前累加值”,然后递归调用左右子树即可
// 题解代码
func sumNumbers(root *TreeNode) int {
// 从 root 节点作为 DFS 起始节点
// “当前累加值” 初始化为 0
return dfs(root, 0)
}
func dfs(root *TreeNode, sum int) int {
// DFS 递归条件处理
if root == nil {
return 0
}
// 计算并更新 “当前累加值”
sum = sum*10 + root.Val
// 如果当前节点的左右子节点都为 nil, 说明当前节点就是叶子节点
// 直接返回 “当前累加值”
if root.Left == nil && root.Right == nil {
return sum
}
// 递归调用左右子树 (并传入 “当前累加值” )
return dfs(root.Left, sum) + dfs(root.Right, sum)
}
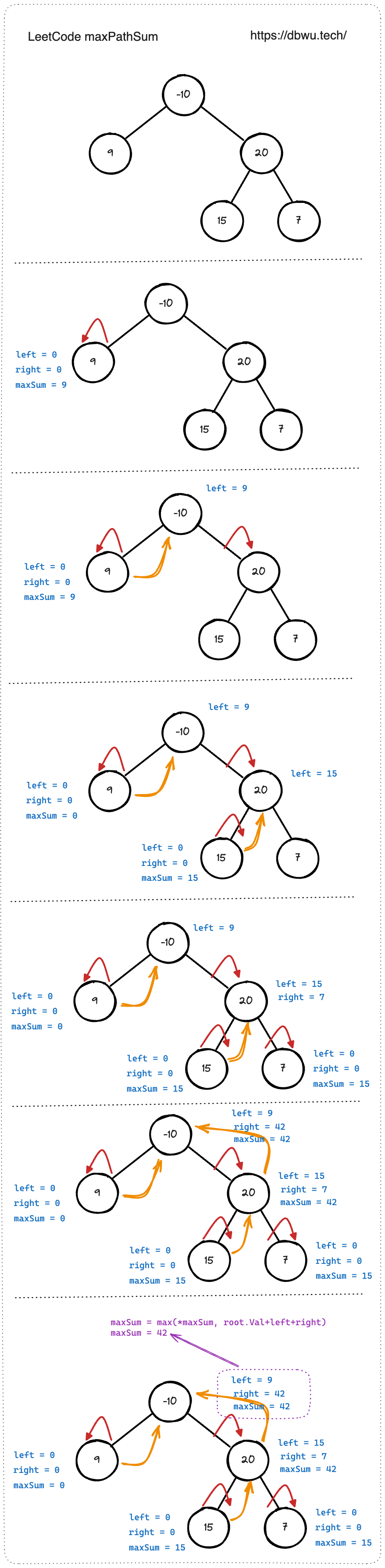
4. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。给你一个二叉树的根节点 root ,返回其 最大路径和 。
如图所示的二叉树中的最大路径和为 6,最大路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
快速套模板:
- 确定 DFS 结束条件和边界处理 (核心),
if root == nil { return } - 确定 DFS 起始节点,也就是参数
root根节点 - 确定单次访问节点,当前节点的左右节点
root.Left,root.Right - DFS 过程中的状态变量如何更新: 使用参数传递 “当前最大路径和”,单个递归过程中,首先分别递归调用左右子树获取左右子树的最大值,然后再和当前节点值计算并更新 “当前最大路径和”
// 题解代码
func maxPathSum(root *TreeNode) int {
// “当前最大路径和” 初始化为一个最小的负数
// 简化边界处理
maxSum := math.MinInt32
// 从 root 节点作为 DFS 起始节点
dfs(root, &maxSum)
return maxSum
}
func dfs(root *TreeNode, maxSum *int) int {
// DFS 递归条件处理
if root == nil {
return 0
}
// 子节点路径和为负数时的边界处理
// 计算左子树的最大路径和
left := max(0, dfs(root.Left, maxSum))
// 计算右子树的最大路径和
right := max(0, dfs(root.Right, maxSum))
// 更新当前最大路径和
*maxSum = max(*maxSum, root.Val+left+right)
// 最大路径只能是根节点 + 左右节点中的任意一个
// 所以必须从左右节点中选择一个节点出来
return root.Val + max(left, right)
}