蛮荆

LeetCode Linked List 刷题模板

2022-03-10 算法

链表特点

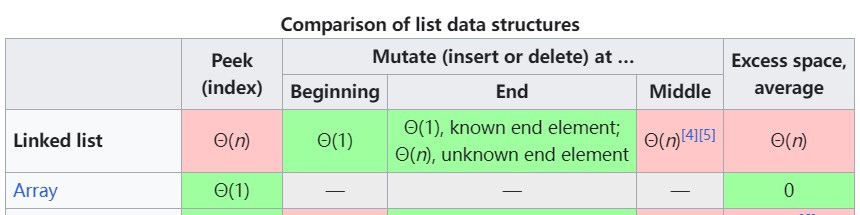
图片来源: https://en.wikipedia.org/

相较于数组，链表的特点如下：

优点

  1. 动态长度：链表的长度可以动态调整 (内存充足的情况下)，不需要像数组预先指定大小
  2. 内存无需连续：链表中的元素在内存中可以是不连续的，提升内存使用灵活性

缺点

  1. 随机访问低效：链表随机访问时，需要从头节点开始遍历，时间复杂度为 O(N)
  2. 插入和删除操作低效：链表中插入和删除元素时，需要移动大量元素，时间复杂度为 O(N)
  3. 额外的存储空间：链表每个节点需要额外的指针来指向下一个节点
  4. 内存局部性较差：链表中的元素在内存中是分散存储的，可能导致缓存不命中，降低访问效率

刷题概述

链表的本质和表现形式都非常简单，就是将不同的节点使用指针连接起来而已。LeetCode 上面链表类大部分问题，如果在纸上画出解题思路和过程，都是非常直观简单的问题，但是真正写代码时，想要快速写出 Bug Free 的代码依然需要花费一番功夫，这其中的症结主要在于两点:

  1. 链表各节点之间依赖于指针连接，如果任意两个节点之间丢失了这个指针，例如将指针错误指向节点，就是导致整个链表无法进行连接，结果必然是错误的，80% 的错误都是因为这个原因导致的
  2. 链表类问题对空间复杂度的要求基本都是 O(1), 这意味着不能引入额外的数据结构来辅助解决问题，例如反转链表问题：要求只能在原地反转，不能引入额外的 栈 (Stack) 来辅助存储节点，然后在栈存储的基础上再反转节点

但是作为高频笔试题类目，链表的重要性不言而喻，必须熟练掌握而且能够快速解决常见的题目，毕竟从面试官的角度来说，求职者可以写不出动态规划、贪心、回溯等题目，但是如果链表类题目都写不出来，那基本上凉凉了。

笨办法

笔者没有太多关于链表类题目的 “技巧” 可以分享，自己在刷题时采用的是最笨的方法，遇到问题时，在纸上画一画链表各节点的状态变化，理清思路，确保没有大的问题之后开始写代码 + 调试过程，然后先保证能写出可以 AC 的代码，最后再对照 LeetCode 官方和其他大佬给出的解题方案学习优化。

概念对齐

市场上关于《数据结构和算法》的图书多如牛毛，每本书中关于相同的概念可能会有不同的名词和描述，为了规范上下文概念，本文将各名词同一如下：

  • 节点: 链表中的任意节点，包含头节点和尾节点
  • 头节点：指向链表第一个节点的指针 (一般指参数传递的指针)
  • 尾节点: 指向链表最后一个节点的指针 (一般用于链表遍历时扫描判断)，尾节点的指针指向 NULL

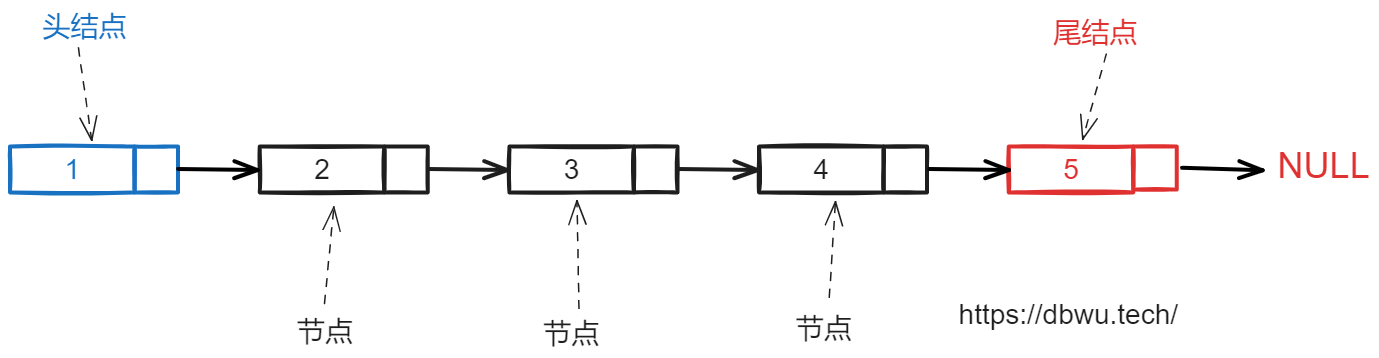
链表基本概念

常见错误

直接使用 head 指针遍历

最常见的错误就是直接使用参数链表 head 头节点指针进行遍历，造成的问题就是随着 head 指针不断遍历链表，head 指针最初指向链表的头节点的连接关系就丢失了。

典型的错误代码如下:

func Solution(head *ListNode) *ListNode {
	// 直接使用 head 遍历链表
    for head != nil {

		...

        head = head.Next
    }

    return head
}

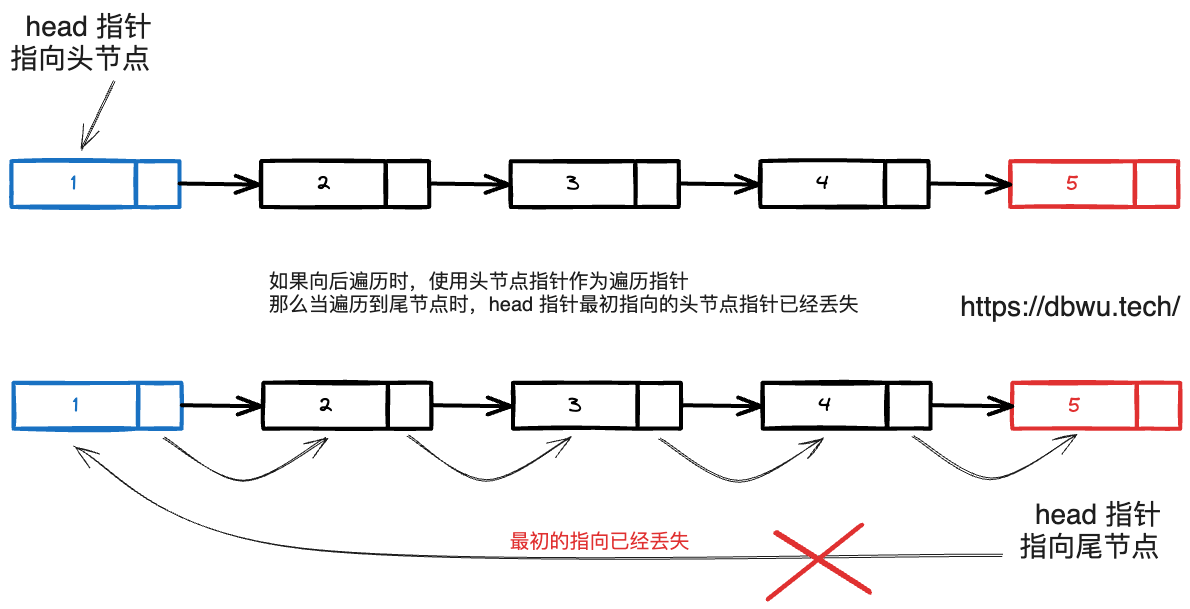
head 指针最终丢失最初的指向

针对这个问题的解决方案是使用一个临时变量来表示扫描链表时的索引指针，这样不管临时指针变量怎么变化，head 指针变量永远指向链表的头节点。

func Solution(head *ListNode) *ListNode {
	// 临时变量 cur 来表示扫描链表时的索引指针
	cur := head

	// 直接使用 cur 遍历链表
    for cur != nil {

		...

        cur = cur.Next
    }

    return head
}

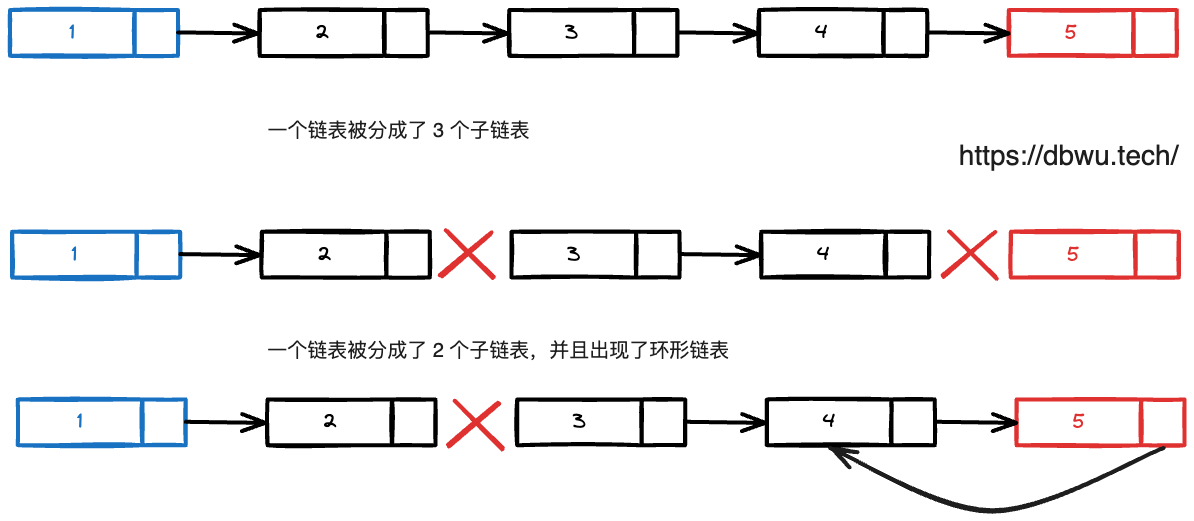
节点指针丢失

遍历链表时，节点和节点之间的连接关系丢失，指针指向了错误的节点，造成的结果就是链表断开了，分成 2 个或多个子链表，更严重的情况下甚至会出现环形链表。

节点指针丢失

头指针为 nil

这个边界检查好就行，链表类问题答案中有 1/3 的代码是边界检查，下面是一个通用类模板:

// 如果节点为空 或者 只有一个节点
// 直接返回就好了，无需处理
if head == nil || head.Next == nil {
    return false
}

通用脚手架代码

虽然 LeetCode 题解一般没有多少代，但是良好的软件工程实践必须保持，单元测试还是要写的，编写 LeetCode 题解代码的同时顺带编写配套的单元测试，可以带来两个好处：

  1. 可以在本地快速运行测试代码，相对 LeetCode 在线编码提升编码效率
  2. 遇到无法通过的测试用例时，可以在本地进行调试，相对 LeetCode 在线 Debug 过程更加可控

所有题解的测试用例可以直接复制粘贴官方和社区提供的，无需自己从零开始编写，所以基本不会有太多的额外时间消耗。

脚手架

笔者根据 LeetCode 官方提供的链表数据结构，提供了两个简单的脚手架函数，用于快速生成测试和调试代码

  1. 根据数组生成对应的链表，可以省去很多的重复性链表代码
  2. 打印指定的链表，可以非常直观地看到当前链表的状态和各个节点的数据，判断链表是否异常，例如节点断开、头指针丢失等问题
// 链表节点定义
type ListNode struct {
	Val  int
	Next *ListNode
}

// 根据指定的数组 (切片) 生成对应的链表并返回头节点
func GenerateListNodesByArray(nums []int) *ListNode {
	dummy := &ListNode{}
	cur := dummy

	for _, val := range nums {
		cur.Next = &ListNode{Val: val}
		cur = cur.Next
	}

	return dummy.Next
}

// 打印指定的链表
func Dump(head *ListNode) *ListNode {
	cur := head

	// 直接使用 cur 遍历链表
    for cur != nil {
		fmt.Printf("%d -> \t", cur.Val)
        cur = cur.Next
    }
	fmt.Println()
}

哨兵模式

最经典的链表解题方案 (或者没有) 之一。

哨兵模式主要应用在以下题型:

  • 需要保留参数 head 头节点的指针并作为返回值返回，例如 “删除链表中的节点” 类型问题
  • 无法提前确认返回值具体是哪个节点，例如 “合并链表” 类型问题，“反转链表” 类型问题

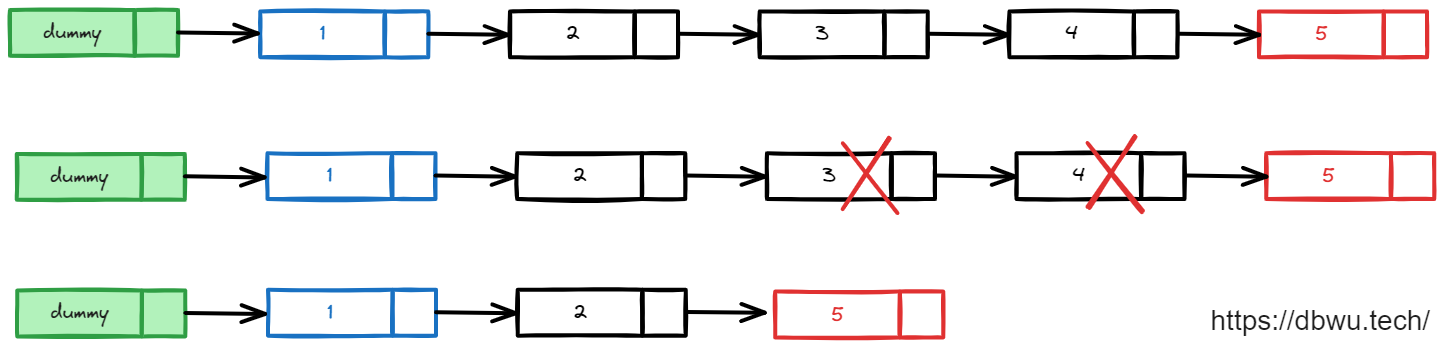
哨兵节点永远指向 Head 头节点

代码模板

使用哨兵模式时，要记住两个必需的核心变量:

  1. 哨兵节点：作为基准保存返回值，其 Next 指向具体的返回值，一般命名为 dummy, 当然也有人称之为 哑巴节点
  2. 扫描节点：从链表头节点开始向后扫描，直到尾节点或符合条件的节点，作用简单来说就是 游标指针，一般命名为 cur

下面是一个典型的使用哨兵模式解题的代码模板:

func Solution(head *ListNode) *ListNode {
	// 哨兵节点指向 头节点
    dummy := &ListNode{Next: head}
	
	// 游标节点
    cur := dummy

	for cur.Next != nil {
		// 执行某些解题逻辑代码

		...
		
		// 更新游标指针
		// 虽然游标指针一直在变化，但是哨兵节点指针的指向没有发生变化
		cur = cur.Next
	}

	// 返回哨兵节点指向的 头节点
    return dummy.Next
}

💡 相关题目

读者可以通过对比题解代码和上文中的模板代码，来体会通过模板快速解题的效率和细节。

1. 合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

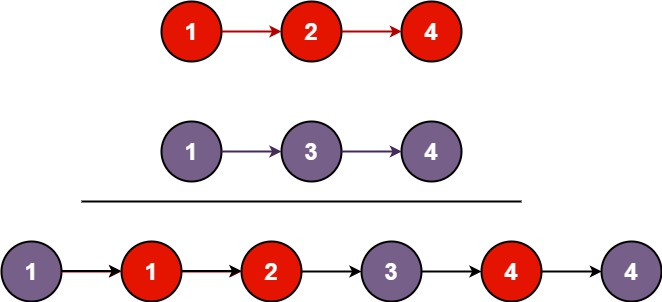
图片来源: https://leetcode.cn

快速套用哨兵节点模板:

  • 一个哨兵节点: 用于存储合并后的链表头节点，并在最后返回
  • 一个游标节点：用于遍历并更新合并后的链表
  • 填充具体的解题逻辑：同时遍历链表 1 和链表 2，将两个链表中的当前较小值插入到合并到后的链表中，同时注意处理好边界条件
// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 100.00% 使用 Go 的用户
// 消耗内存分布击败 81.81% 使用 Go 的用户
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
	// 哨兵节点
	dummy := &ListNode{Val: 0}
	// 游标节点
	cur := dummy

	for l1 != nil && l2 != nil {
		if l1.Val < l2.Val {
			cur.Next = l1
			l1 = l1.Next
		} else {
			cur.Next = l2
			l2 = l2.Next
		}
		cur = cur.Next
	}

	if l1 == nil {
		cur.Next = l2
	} else {
		cur.Next = l1
	}

	return dummy.Next
}

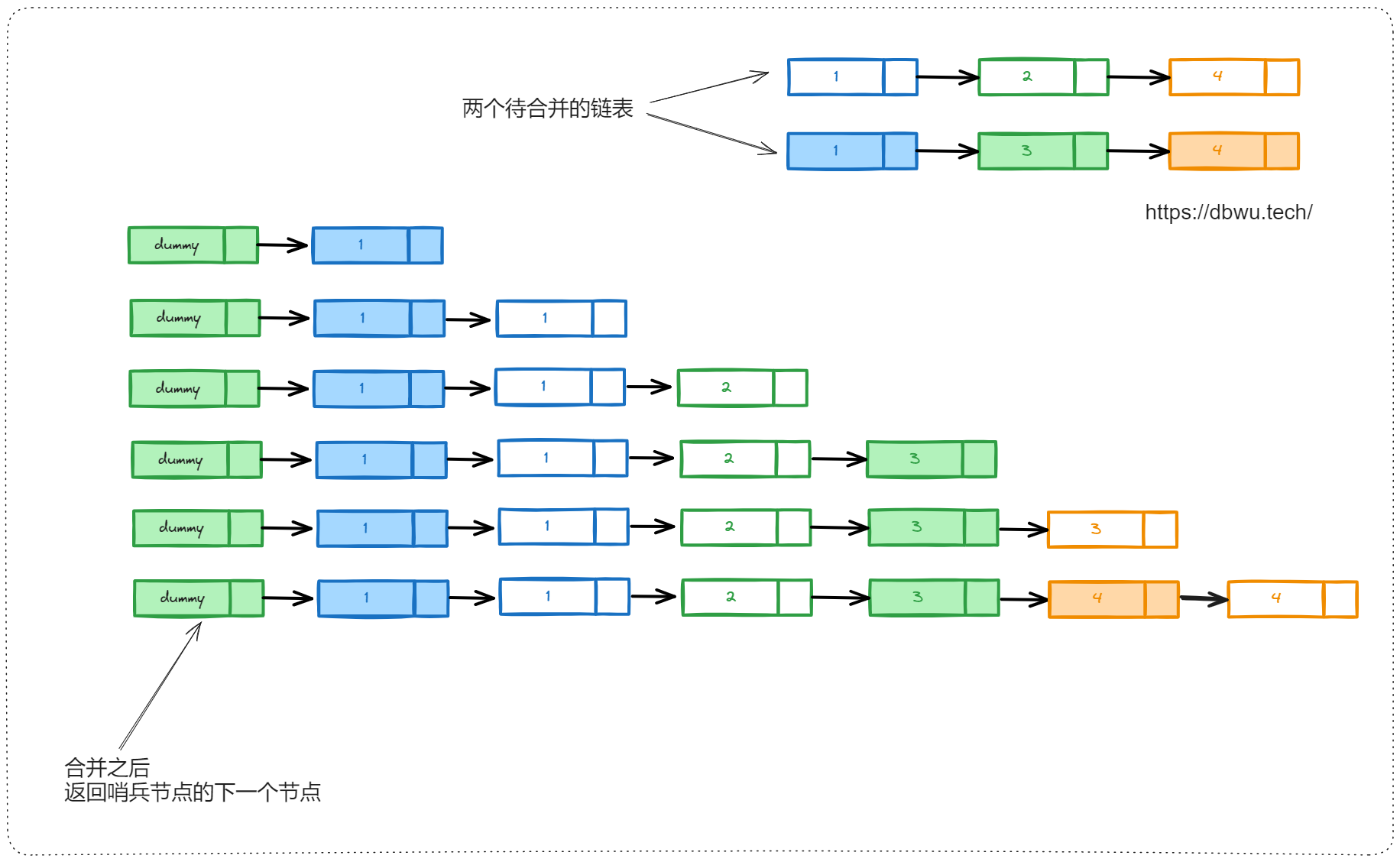
下面是题解代码执行过程，其中每一步合并后的节点，使用不同的颜色和填充进行区分：

合并两个有序链表执行过程

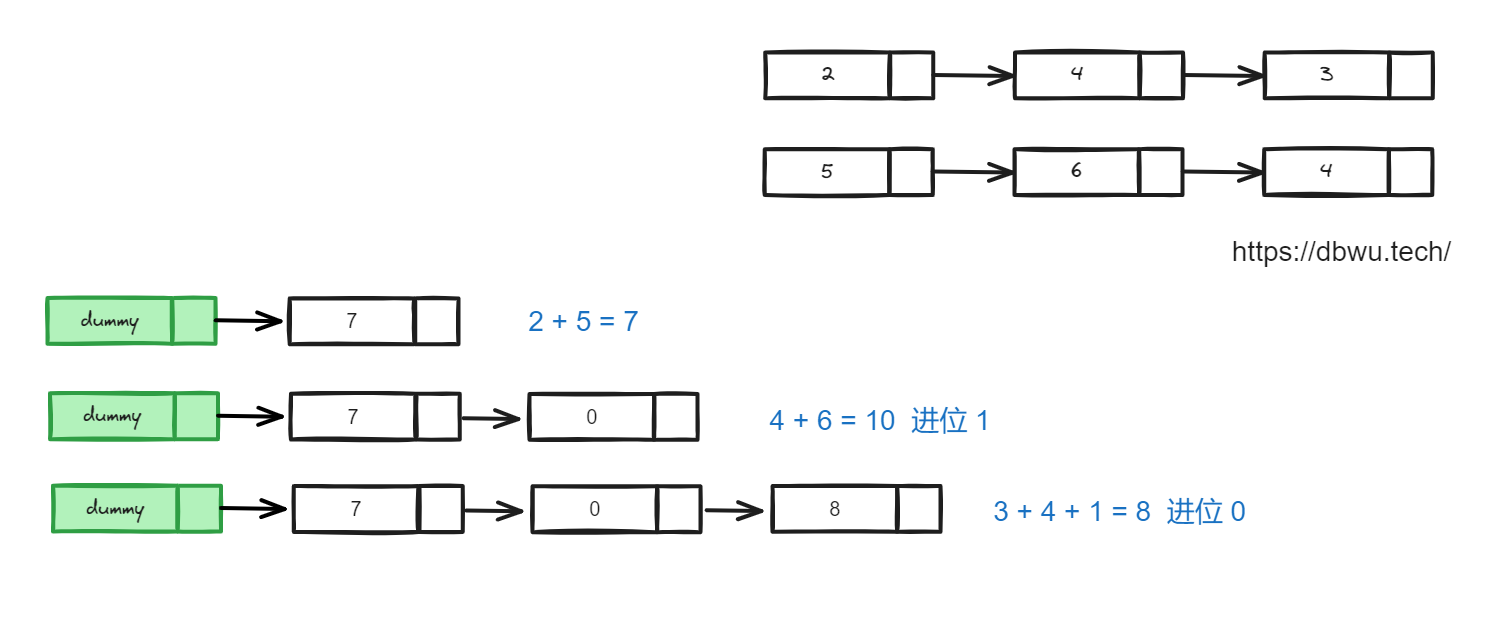
2. 两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

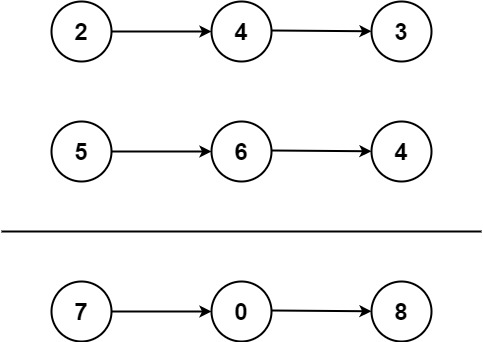
图片来源: https://leetcode.cn

这道题的本质也是 “合并两个链表”，不过和上一题的区别在于合并的不是两个链表中单独的节点，而是对应节点上面的值。

快速套用哨兵节点模板:

  • 一个哨兵节点: 用于存储合并后的头节点并在最后返回
  • 一个游标节点：用于遍历并更新合并后的链表
  • 填充具体的解题逻辑：同时遍历链表 1 和链表 2，取出两个链表的当前节点进行相加，并将结果放入合并后的链表的下一个节点，同时注意处理好 “进位制” 和边界条件
// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 57.35% 使用 Go 的用户
// 消耗内存分布击败 43.80% 使用 Go 的用户
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
	// 哨兵节点
    dummy := &ListNode{Val: 0}
	// 游标节点
    cur := dummy

    n1, n2, carry := 0, 0, 0

    for l1 != nil || l2 != nil || carry != 0 {
		// 计算链表 1 的当前值
        if l1 == nil {
            n1 = 0
        } else {
            n1 = l1.Val
            l1 = l1.Next
        }

		// 计算链表 2 的当前值
        if l2 == nil {
            n2 = 0
        } else {
            n2 = l2.Val
            l2 = l2.Next
        }

		// 当计算出来的新节点放到当前节点后面
        cur.Next = &ListNode{Val: (n1 + n2 + carry) % 10}

		// 计算是否需要进位
        carry = (n1 + n2 + carry) / 10

		// 更新当前节点
        cur = cur.Next
    }

    return dummy.Next
}

两个链表相加执行过程

3. 两两交换链表中的节点

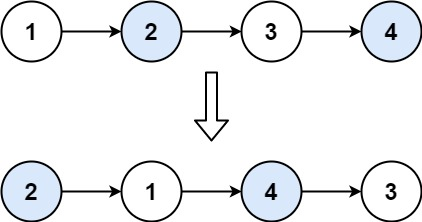
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

图片来源: https://leetcode.cn

快速套用哨兵节点模板:

  • 一个哨兵节点: 用于存储交换后的头节点并在最后返回 (也就是原始链表的第二个节点)
  • 一个游标节点：用于遍历并更新合并后的链表
  • 填充具体的解题逻辑：使用游标指针遍历链表，当游标指针的下一个节点和下下一个节点同时不为 nil 时，交换两者
// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 100.00% 使用 Go 的用户
// 消耗内存分布击败 76.28% 使用 Go 的用户
func swapPairs(head *ListNode) *ListNode {
	// 哨兵节点
	dummy := &ListNode{Next: head}
	// 游标节点
	cur := dummy

	// cur 必须从 dummy 开始
	// 这样才可以更换 dummy.Next (head) 指针的指向
	// 因为最终要返回 dummy.Next

	// cur 初始化时指向 dummy
	// 但是在遍历过程中会不断发生变更
	// 而 dummy 只会在第一次指向 head.Next.Next 之后就不会发生改变
	// 正确的答案，最终的 dummy.Next 指向的是源链表的第二个节点
	for cur.Next != nil && cur.Next.Next != nil {
		node1 := cur.Next
		node2 := cur.Next.Next
		cur.Next = node2
		node1.Next = node2.Next
		node2.Next = node1
		cur = node1
	}

	return dummy.Next
}

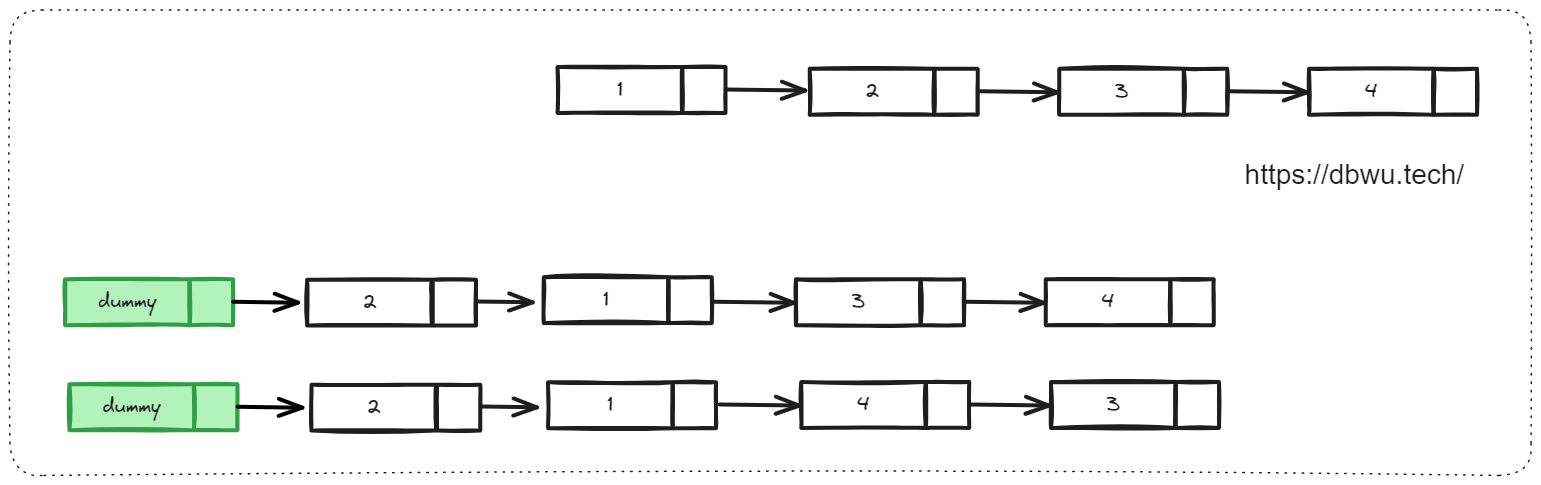
两两交换链表中的节点 - 执行过程

双哨兵模式

有的时候，需要保存的基准节点可能不止一个，怎么办？那就需要多少个基准节点，就使用多少个哨兵节点就好了，例如下面的这道题。

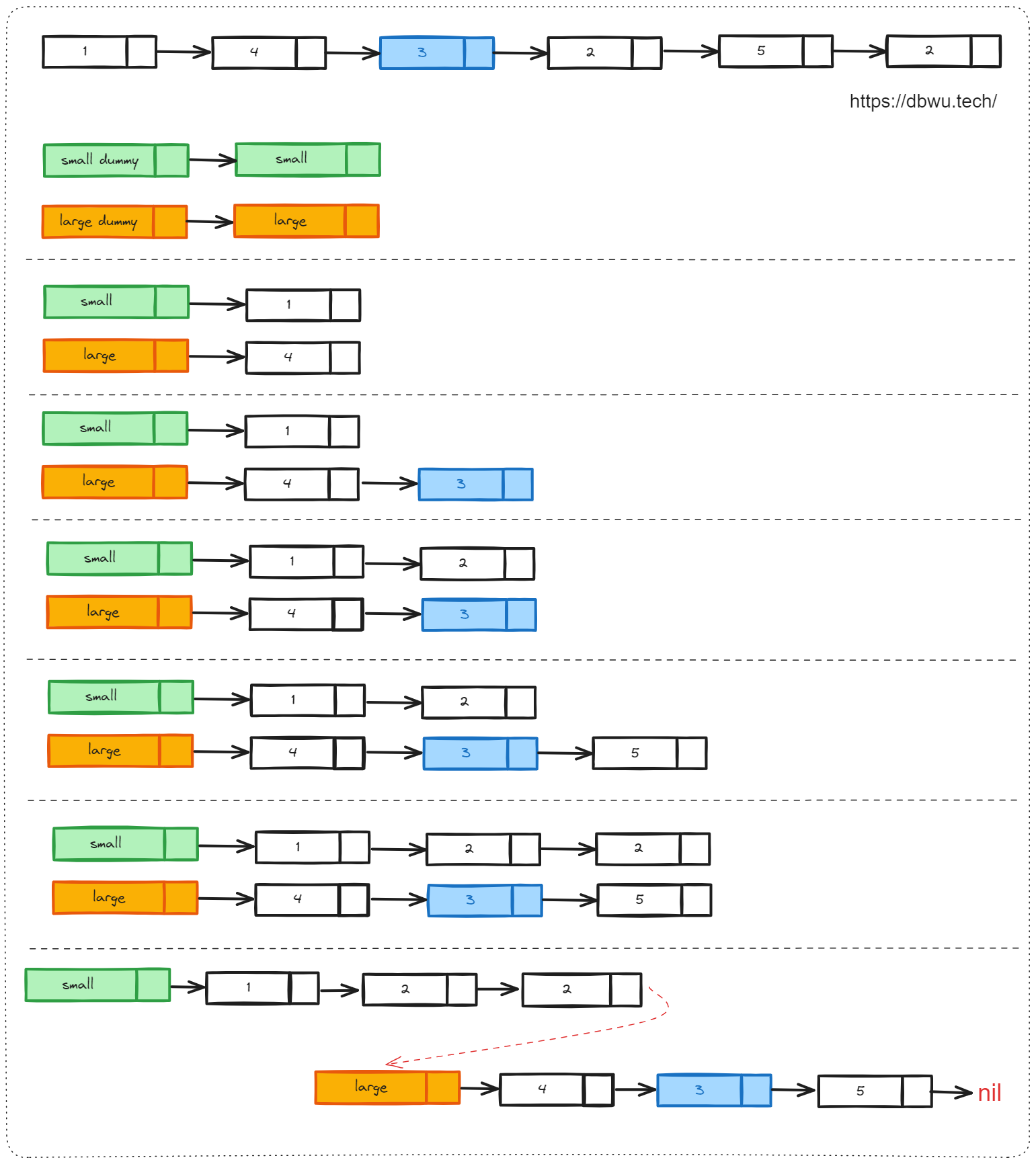
1. 分隔链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。你应当 保留 两个分区中每个节点的初始相对位置。

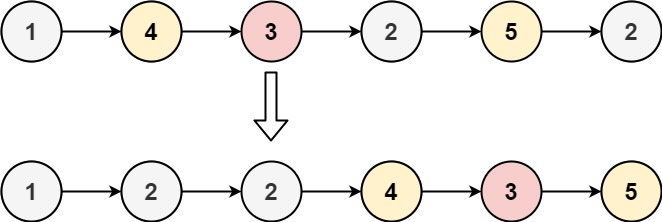
图片来源: https://leetcode.cn

题目的要求很简单，就是将小于 X 的节点链接起来形成一个链表，然后将大于等于 X 的节点链接起来形成一个链表，然后将两个链表前后串起来即可，不需要实现排序。

快速套用哨兵节点模板:

  • 两个哨兵节点: 将小于 X 的所有节点单独形成一个链表 small, 将大于等于 X 的所有节点单独形成一个链表 large, 声明两个哨兵节点分别指向 small 链表的头节点和 large 链表的头节点
  • 一个游标节点：用于遍历并更新合并后的链表，因为最终返回值是 small 链表的头节点，所以可以直接使用参数 head 指针作为游标指针
  • 填充具体的解题逻辑：使用游标指针遍历链表，将小于 X 的节点插入到链表 small 末尾, 将大于等于 X 的节点插入到链表 large 末尾，遍历完成之后，连接 small 链表和 large 链表，并切断 large 链表的尾指针指向
func partition(head *ListNode, x int) *ListNode {
	// 哨兵节点：指向 small 链表的头节点
	smallDummy := &ListNode{}
	// 哨兵节点：指向 large 链表的头节点
	largeDummy := &ListNode{}

	// 小于 X 的所有节点形成的链表
	small := smallDummy
	// 大于等于 X 的所有节点形成的链表
	large := largeDummy

	// 直接使用 head 作为游标指针
	for head != nil {
		if head.Val < x {
			small.Next = head
			small = small.Next
		} else {
			large.Next = head
			large = large.Next
		}
		head = head.Next
	}

	// 切断 large 链表的尾指针
	// 例如源链表为 1 -> 4 -> 3 -> 2 -> 5 -> 2, X = 3
	// 那么在分割完成后
	// small 链表为 1 -> 2 -> 2 -> 5 ...
	// large 链表为 4 -> 3 -> 5 -> 2 ...
	// 这时就需要将 large 链表末尾指针给切断，否则就形成了 “环形链表”
	large.Next = nil
	
	// 将 small 链表连接到 large 链表
	small.Next = largeDummy.Next

	// 返回 small 链表的头节点
	return smallDummy.Next
}

两个链表分隔 + 合并执行过程

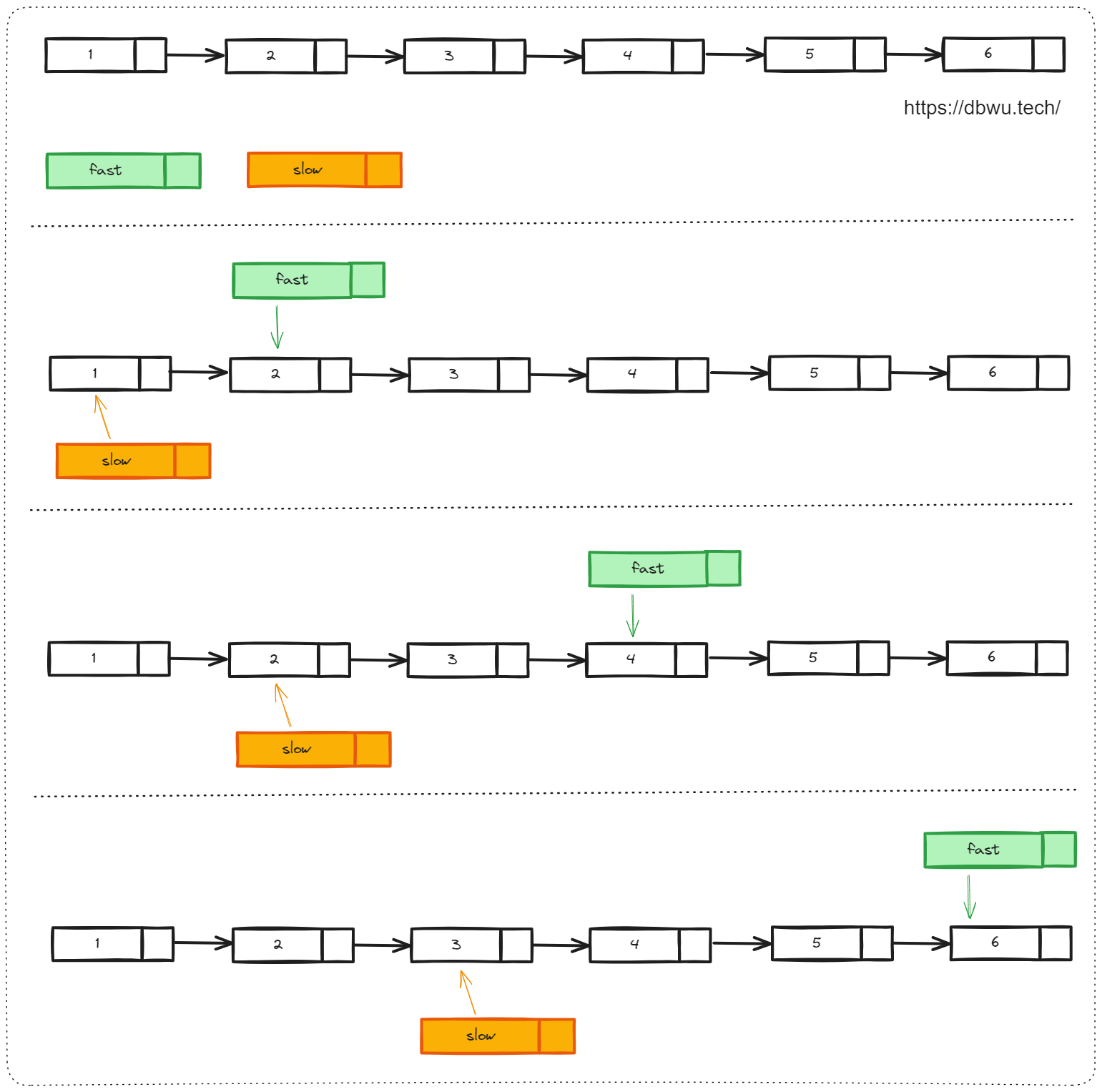
快慢指针

最经典的链表解题方案 (如果有的话) 之二。

顾名思义，快慢指针就是使用两个指针来遍历链表，快指针走的快 (例如每次扫描两个及以上节点)，慢指针走的慢 (例如每次扫描一个节点)，严格意义上来说，“快慢指针” 属于 “双指针” 的解题类型范畴，之所以在这篇关于链表类的文章中单独拎出来，主要有两点：

  1. 链表的节点就是由指针连接起来的，天然适用于快慢指针来遍历，比如我们可以使用 快慢指针来简洁实现 “找到链表的中间节点”
  2. 链表类型的某些问题，使用快慢指针是最简洁优雅的方案，例如经典的 “判断链表中是否存在环问题”

代码模板

func Solution(head *ListNode) bool {
	// 通用边界检查
    if head == nil {
        return false
    }

	// 初始化快、慢两个指针
    slow, fast := head, head.Next
	// 主要这里的边界检查
	// 因为快指针每次走两步，需要需要检测两步之内的节点是否为 nil
	// 慢指针无需执行边界检查
	// 因为只要快指针不为 nil, 慢指针肯定也不会为 nil
    for fast != nil && fast.Next != nil {
		// 执行某些解题逻辑代码

		...

		// 快指针每次走 2 步 
        fast = fast.Next.Next
		// 慢指针每次走 1 步
        slow = slow.Next
    }

    return false
}

快慢指针执行过程

💡 相关题目

读者可以通过对比题解代码和上文中的模板代码，来体会通过模板快速解题的效率和细节。

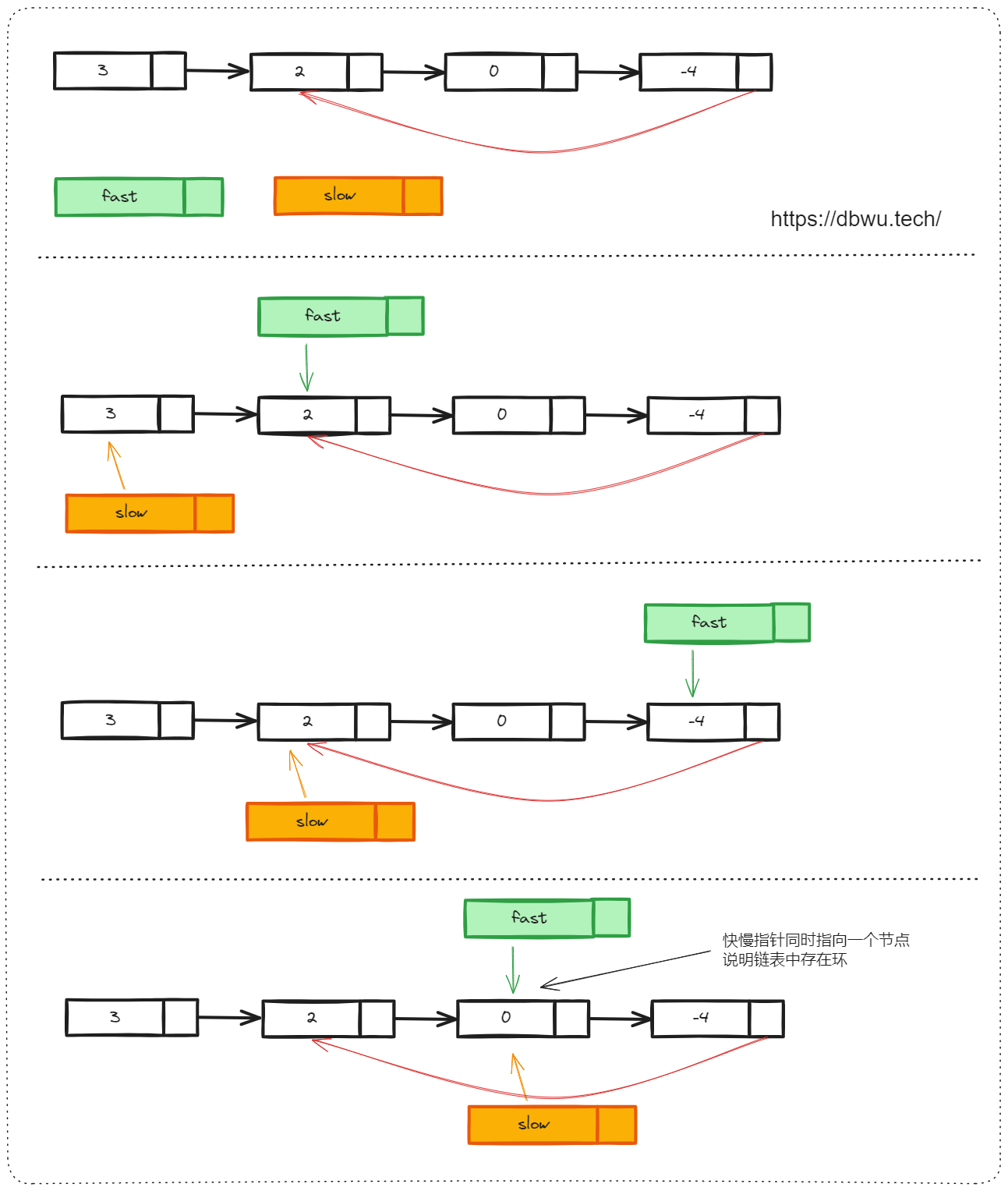
1. 环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

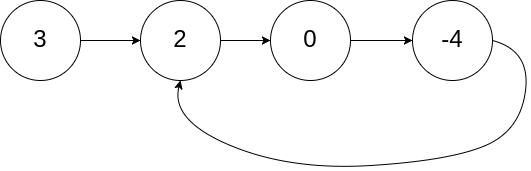
图片来源: https://leetcode.cn

快速套用快慢指针解题模板:

  • 定义快慢指针: 快指针每次扫描 2 个节点，慢指针每次扫描 1 个节点
  • 填充具体的解题逻辑：因为慢指针扫描到链表一半长度的时候，快指针就扫描到链表的末尾了，所以如果链表存在环的话，那么快慢两个指针一定会相遇

还有一个细节需要注意: 即使只有一个节点，也可能是环形链表，所以下面的代码无法通过全部测试。

if head == nil || head.Next == nil {
    return false
}

// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 58.65% 使用 Go 的用户
// 消耗内存分布击败 79.63% 使用 Go 的用户
func hasCycle(head *ListNode) bool {
	// 需要注意的是，即使只有一个节点，也可能是环形链表
	// 所以这段代码无法通过测试
	// if head == nil || head.Next == nil {
	// 	return false
	// }
	if head == nil {
		return false
	}

	// 快指针先走一步，避免链表只有一个节点时误判为环形链表
	slow, fast := head, head.Next
	for fast != nil && fast.Next != nil {
		if slow == fast {
			return true
		}
		fast = fast.Next.Next
		slow = slow.Next
	}

	return false
}

链表中检测是否存在环 - 执行过程

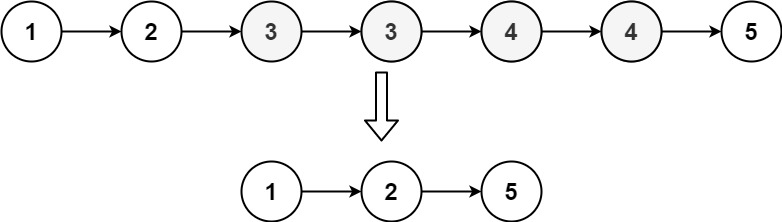
2. 删除重复节点

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

图片来源: https://leetcode.cn

// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 59.62% 使用 Go 的用户
// 消耗内存分布击败 34.55% 使用 Go 的用户
func deleteDuplicatesIteratively(head *ListNode) *ListNode {
	if head == nil {
		return head
	}

	dummy := &ListNode{Next: head}
	// 这里哨兵节点极大提高了代码可读性
	// 直接从 cur.Next (也就是头节点) 开始
	// 这样即使头节点就是重复元素，也可以直接将其删除，然后将哨兵节点的 Next 指针指向到第一个不重复的节点
	cur := dummy

	for cur.Next != nil && cur.Next.Next != nil {
		if cur.Next.Val == cur.Next.Next.Val {
			x := cur.Next.Val
			// 删除掉所有和当前节点值相等的后续节点
			// 注意这里不改变 cur 指针的指向，而是直接改变 cur.Next 指针的指向
			// 也就是说，每次判断的都是以 [下个节点] 和 [下下个节点]
			// 当前节点从哨兵节点开始，本身就是不重复的值，因为重复的值在节点连接过程中都被删除掉了
			for cur.Next != nil && cur.Next.Val == x {
				cur.Next = cur.Next.Next
			}
		} else {
			cur = cur.Next
		}
	}

	return dummy.Next
}

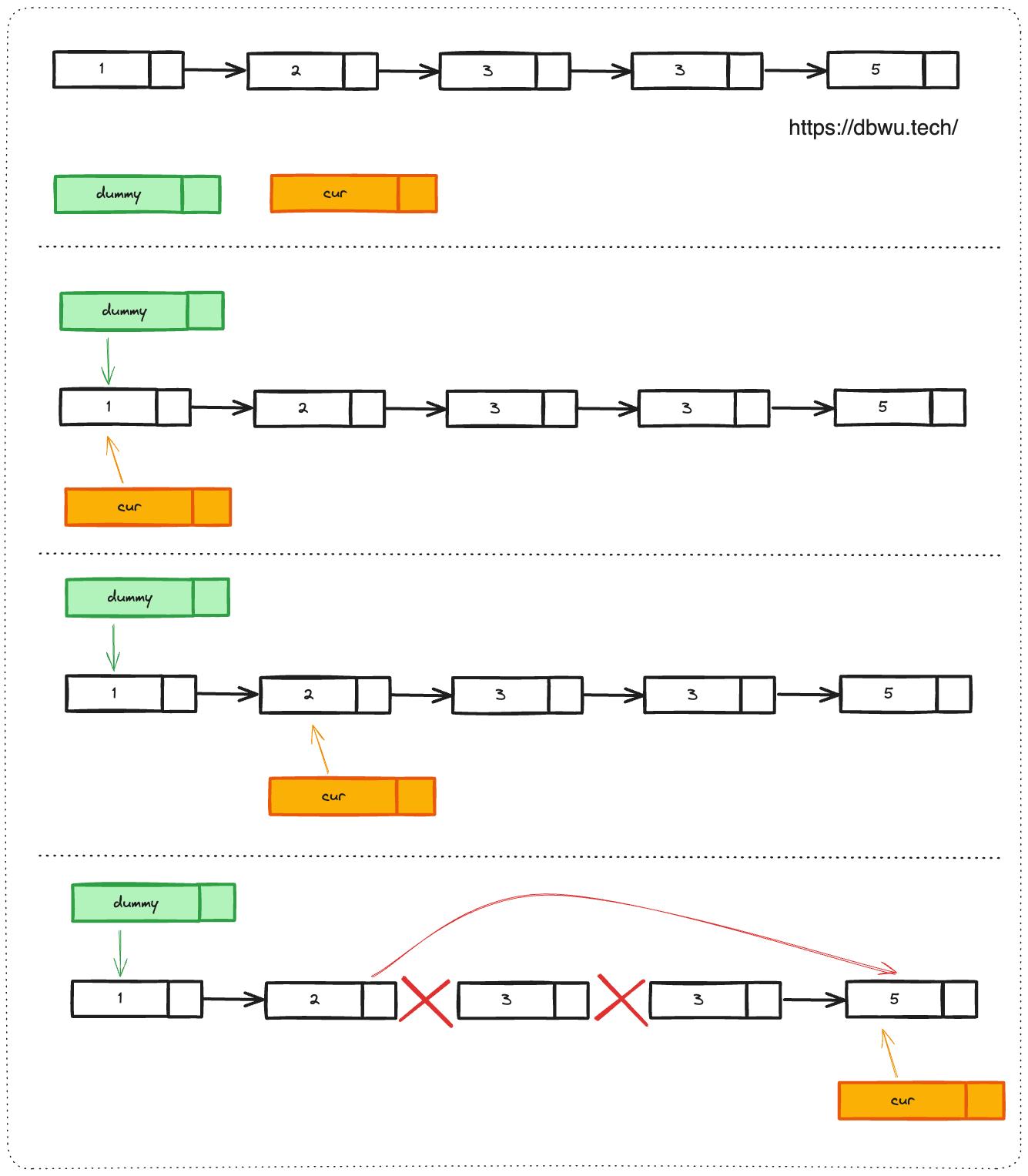
删除重复节点 - 执行过程

虽然上面的题解代码中并没有使用到快慢指针，而只是使用一个 cur 指针作为遍历指针，但其实整个思路和快慢指针是一致的，我们可以外部的 cur 指针遍历循环看作是慢指针，每次走一步，将内部的 cur 指针遍历看作是快指针，每次都 N 步 (N 等于重复的数字个数)，感兴趣的读者可以将两层循环替换为快慢两个指针来扫描，体验一下思路相通的妙处。除了快慢指针之外，这个解题方案还用到了哨兵哨兵，也是一道经典题。

题外话: 如果将链表换做数组，那么删除所有重复元素非常简单，所以唯一有差异或者容易出错的地方还是在于链表这种数据结构，

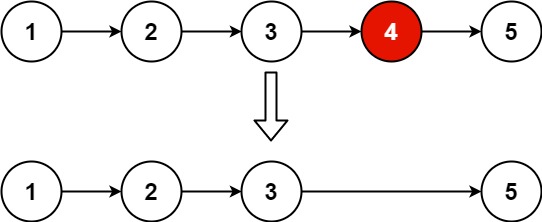
3. 删除倒数第 N 个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

图片来源: https://leetcode.cn

快速题解:

删除倒数第 N 个节点，反过来看，倒数第 N 个节点也就是整数第 M - N 个节点，其中 M 表示链表的长度，所以解题可以分为两步:

  1. 计算链表的长度 M
  2. 从前向后遍历链表，删除第 M - N 个节点
// 计算链表的长度 M
func getLength(head *ListNode) int {
	length := 0
	for head.Next != nil {
		head = head.Next
		length++
	}
	return length
}

// 删除链表第 M - N 个节点
func removeNthFromEnd(head *ListNode, n int) *ListNode {
	if n <= 0 {
		return head
	}

	// 熟悉的哨兵节点
	dummy := &ListNode{0, head}
	length := getLength(head)
	
	// 熟悉的游标节点
	cur := dummy
	for i := 0; i < length-n+1; i++ {
		cur = cur.Next
	}

	cur.Next = cur.Next.Next

	return dummy.Next
}

优化题解:

在上面的题解中，我们一共遍历了两次链表，但是题目要求只遍历一次链表来解决问题，所以这道题肯定还存在更快速 “解题技巧”。

这里我们依然可以 引入快慢针对的思路：既然倒数第 N 个节点就是正数的 M - N 个节点，那么我们设定 一个快指针先走 N 步，然后设定一个慢和快指针以相同的步幅一起走 (指针每次向前移动一次)，这样等到快指针移动到末尾时，慢指针正好移动到第 M - N 个节点，也就是倒数第 N 个节点，删除慢指针指向的节点即可。

注意细节：因为头节点就是第一个节点，所以这里慢指针应该指向的是哨兵节点。

// 题解代码
// 非 VIP 用户提交
// 执行用时分布击败 100.00% 使用 Go 的用户
// 消耗内存分布击败 76.13% 使用 Go 的用户
func removeNthFromEnd(head *ListNode, n int) *ListNode {
	if n <= 0 {
		return head
	}

	// 哨兵节点
	dummy := &ListNode{0, head}
	// 注意快慢指针的初始化指向
	fast, slow := head, dummy

	// 快指针先走 N 步
	for i := 0; i < n && fast != nil; i++ {
		fast = fast.Next
	}

	// 然后快慢指针一起走
	for fast != nil {
		slow = slow.Next
		fast = fast.Next
	}

	// 当快指针扫描到链表结尾时
	// 慢指针指向的正好是需要删除的节点的前置节点
	slow.Next = slow.Next.Next

	return dummy.Next
}

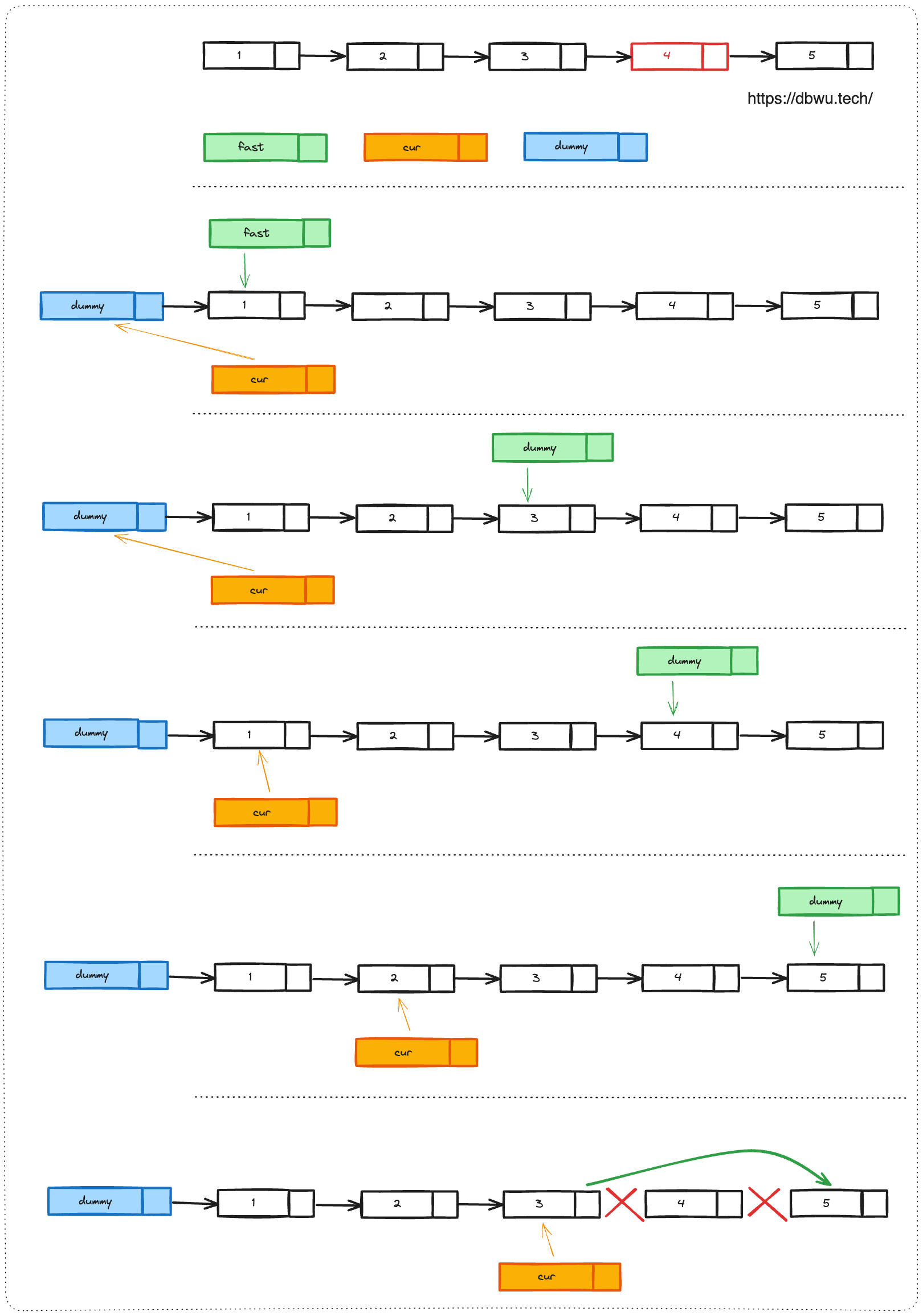
删除倒数第 N 个节点 - 执行过程

不得不说，这个题真是快慢指针的经典应用了。

反转模式

涉及到原地链表反转类问题，尽可能不要使用额外的数据结构和辅助空间，属于减分项。

反转操作过程中需要注意的是：两两节点交换反转之后，不要丢掉指针和节点的连接关系，以及头节点和尾节点的边界处理。

Go 语言的骚操作

交换两个链表节点，Go 语言实现非常简单，其他语言需要一个可能临时 tmp 节点来作为中转。

实际算法笔试中，尽量不要写带有强烈的语言特性 (语法糖) 的代码，而应该写出 “语法更加通用” 的代码，也就是你给出的题解算法，不论用什么代码实现，看起来都是差不多的。

func reverseListForGolang(head *ListNode) *ListNode {
	var prev *ListNode

	for head != nil {
		prev, head, head.Next = head, head.Next, prev
	}

	return prev
}

💡 相关题目

读者可以通过对比题解代码和上文中的模板代码，来体会通过模板快速解题的效率和细节。

1. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

图片来源: https://leetcode.cn

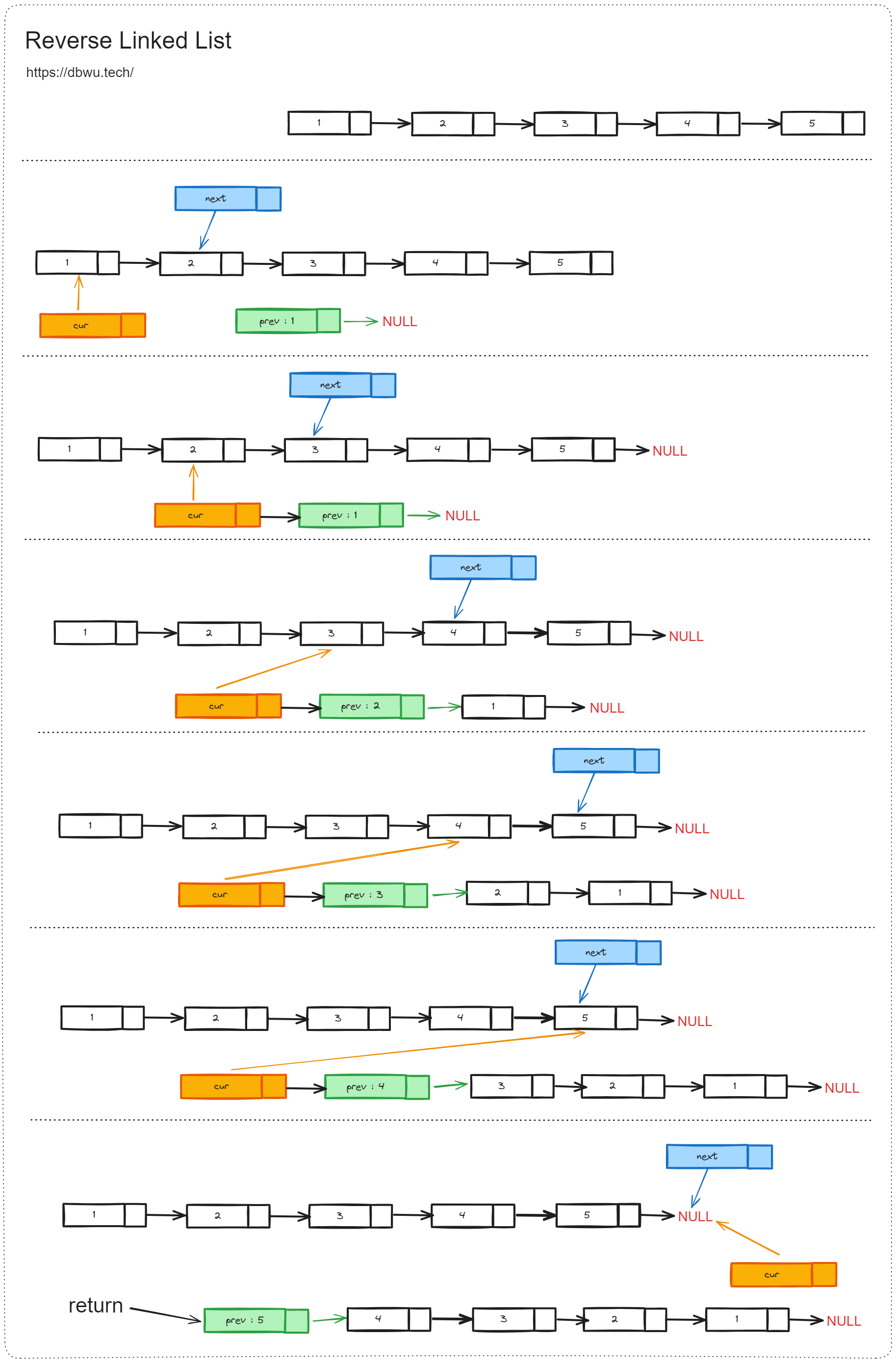
定义三个指针变量分别指向:

  • prev : 当前节点的前一个节点指针，初始化时为 nil
  • cur : 当前节点指针，游标指针，初始化时指向链表头节点
  • next : 当前节点的下一个节点指针，遍历时不断更新

链表扫描结束之后，prev 指针变量指向反转后的链表头节点，直接返回即可。

func reverseList(head *ListNode) *ListNode {
    var prev *ListNode
    cur := head

    for cur != nil {
        next := cur.Next
        cur.Next = prev
        prev = cur
        cur = next
    }

    return prev
}

反转链表执行过程

2. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

图片来源: https://leetcode.cn

如果从反转链表的角度来看的话，这个题可以变种为：反转链表的部分节点，因为前文中已经给到题解，这里就不再赘述了。

小结

熟练掌握本文中提到的两套刷题模板：哨兵节点 + 快慢指针，从此百分之八十的链表类题目刷起来犹如切瓜砍菜般简单。

都看到这里了，不点个赞再走么？

转载申请

本作品采用 知识共享署名 4.0 国际许可协议 进行许可，转载时请注明原文链接，图片在使用时请保留全部内容，商业转载请联系作者获得授权。