LeetCode Sliding Window 刷题模板
📖 概述
滑动窗口(Sliding Window)是一种用于解决数组/字符串相关问题的常见技巧,通过维护一个大小可以伸缩的窗口来执行具体操作,随着窗口在数组/字符串上移动,根据窗口的变化来执行具体的操作。
刷题模板
滑动窗口算法执行的基本步骤:
- 初始化左指针 left 和右指针 right,并且初始化结果变量
- 移动右指针,扩大窗口大小,直到满足特定条件 (窗口内的元素满足某种条件 或 达到数组/字符串的末尾)
- 移动左指针,缩小窗口大小 (直到不再满足特定条件) 同时更新结果变量
- 重复步骤 2 和 3,直到右指针达到数组/字符串的末尾
下面是一个典型的滑动窗口执行过程示例:
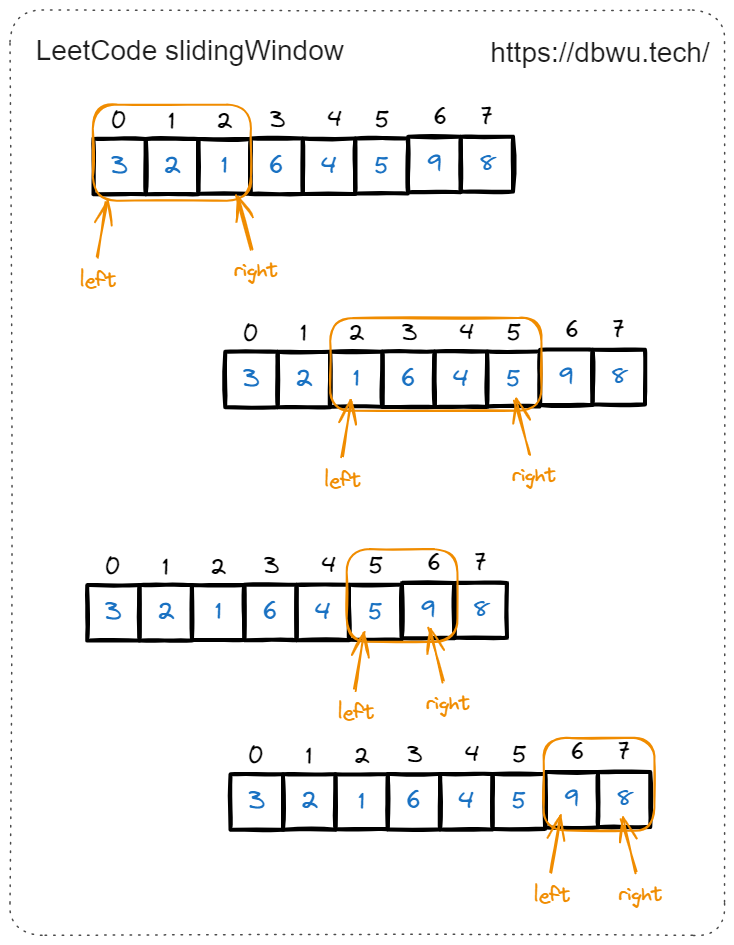
// 滑动窗口刷题代码模板
func slidingWindow(nums []int) int {
// 初始化左右指针
left, right := 0, 0
// 初始化结果变量
result := 0
// 迭代右指针
for right < len(nums) {
// 更新窗口状态
// 移动左指针,收缩窗口大小,更新结果变量
// 更新右指针,扩大窗口大小
}
return result
}
💡 典型题目
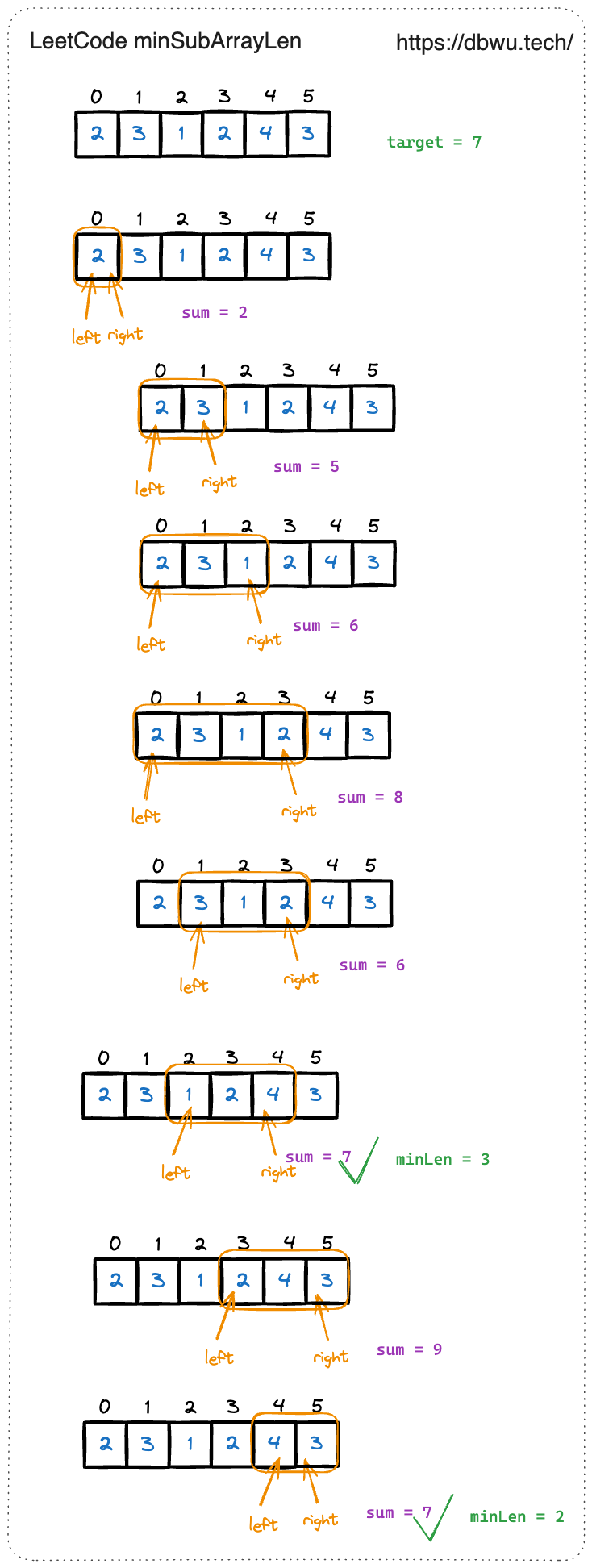
1. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
# 示例来源: https://leetcode.cn/
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
解题思路:
- 初始化左指针 left 和右指针 right,并且初始化结果最小长度
- 移动右指针,扩大窗口大小,直到满足特定条件 (窗口内的元素和大于等于目标参数 或 达到数组的末尾)
- 移动左指针,缩小窗口大小 (窗口内的元素和小于目标参数) 同时更新结果变量
- 重复步骤 2 和 3,直到右指针达到数组的末尾
// 题解代码
func minSubArrayLen(target int, nums []int) int {
// 初始化最小长度为数组长度 + 1
minLen := len(nums) + 1
sum, left := 0, 0
// 移动右指针
for right := range nums {
sum += nums[right]
// 找到符合条件的子数组时,开始收缩窗口大小
for sum >= target {
minLen = min(minLen, right-left+1)
sum -= nums[left]
left++
}
}
// 如果最小长度依然等于数组长度 + 1
// 说明数组中不存在符合条件的子数组
if minLen > len(nums) {
return 0
}
return minLen
}
func min(x, y int) int {
if x < y {
return x
}
return y
}
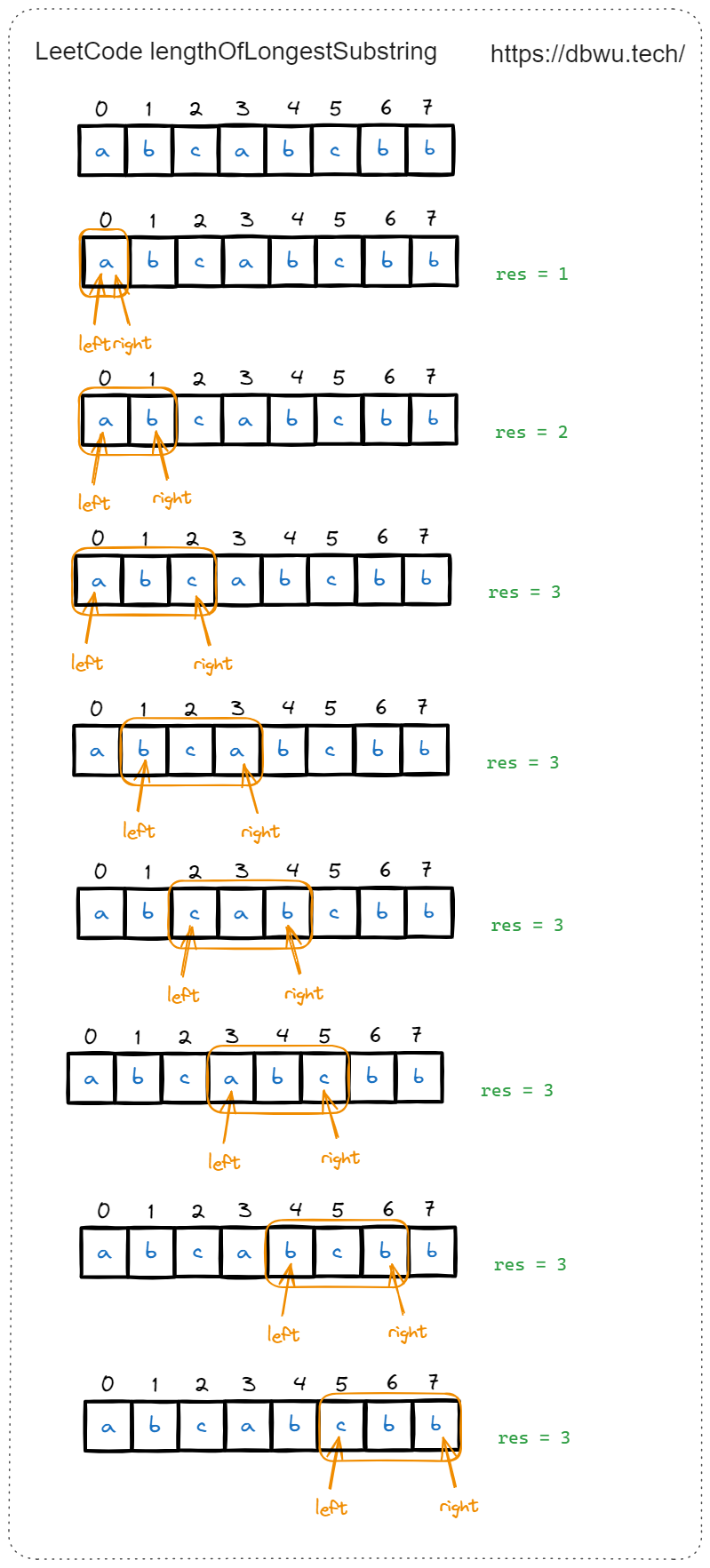
2. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
# 示例来源: https://leetcode.cn/
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
解题思路:
- 初始化左指针 left 和右指针 right,并且初始化结果最小长度,同时维护一个 Map 作为窗口内的重复字符检测
- 移动右指针,扩大窗口大小,直到满足特定条件 (窗口内的元素出现重复 或 达到字符串的末尾)
- 移动左指针,缩小窗口大小 (窗口内的元素没有重复) 同时更新结果变量.
- 重复步骤 2 和 3,直到右指针达到字符串的末尾
// 题解代码
func lengthOfLongestSubstring(s string) int {
// 题目声明字符串 s 由英文字母、数字、符号和空格组成
// 所以这里使用一个长度为 256 的数组来模拟 Map 功能
var win [256]int
res, n := 0, len(s)
// 声明左右指针
for left, right := 0, 0; right < n; right++ {
c := s[right]
// 更新窗口
win[c]++
// 遇到重复的字符时,开始收缩窗口大小
for win[c] > 1 {
win[s[left]]--
left++
}
// 更新已知的最大窗口
res = max(res, right-left+1)
}
return res
}