LeetCode Stack 刷题模板
📖 概述
在计算机科学中,栈 (Stack) 是一种抽象数据结构,主要针对集合类数据 (最常见的是数组) 进行两种操作:
- Push (入栈): 将元素添加到集合中
- Pop (出栈): 将最近加入的元素从集合中删除
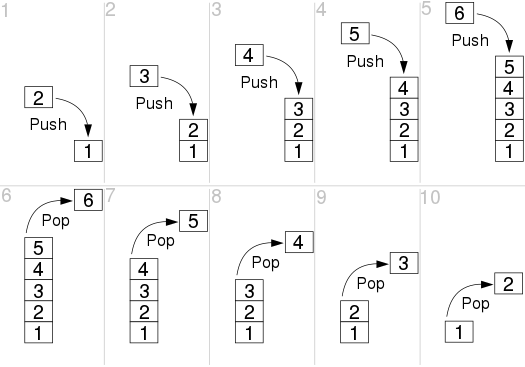
如上图所示的栈结构中,初始化栈内元素为 1,紧接着进行了两轮操作:
- 将元素 2, 3, 4, 5, 6 分别入栈 (也就是图中的 1, 2, 3, 4, 5 对应的小图)
- 将元素 6, 5, 4, 2, 2 分别出栈 (也就是图中的 6, 7, 8, 9, 10 对应的小图)
因为入栈和出栈的操作顺序正好相反,所以栈的顺序简称为 “后进先出”,单次缩写为 LIFO (Last In, First Out)。
🛠️ 容易出错的细节
虽然栈 (Stack) 数据结构简单直观,易于理解,但是实践中还是有几个常见的细节会引发 Bug。
- 入栈和出栈操作顺序错误
- 边界异常: 栈为空时出栈、栈溢出 (栈已满时入栈)
- 无限循环或递归: 没有及时出栈或者出栈逻辑实现错误
- 元素类型异常: 入栈之前应该检测元素类型,尤其是当元素为接口类型时,一定要检测入栈元素是否实现了特定接口,避免运行时错误
Golang Stack
Go 语言中并没有专门的 Stack 数据类型,大部分情况下使用切片 Slice 作为栈 (Stack) 的实现,使用方法和其他主流编程语言相比,属于实现别扭且难用型,建议读者配合日常使用的编辑器对应的插件 (高亮提示+代码自动补全) 来编写代码。
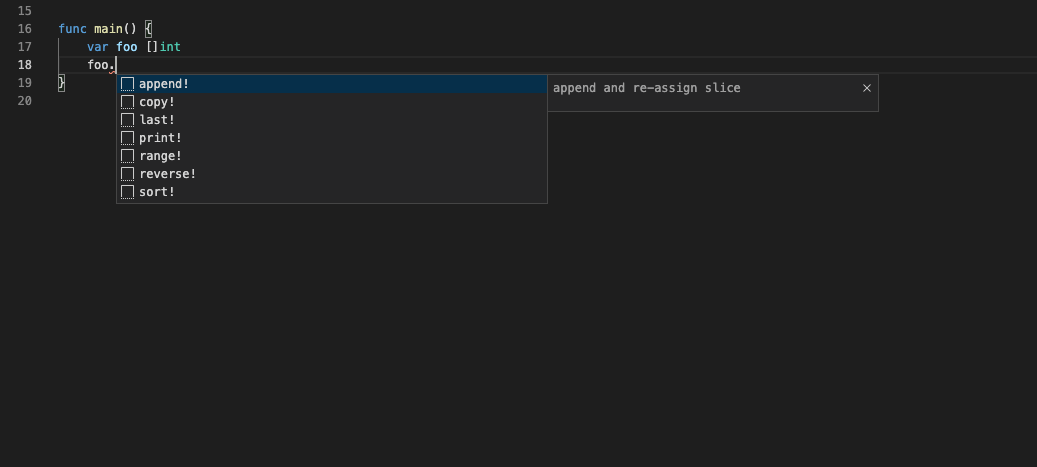
如图所示为 VSCode 中操作 Stack 数据结构时对应的代码自动补全,可以调用的 append 方法实现入栈操作,调用 last 方法获取栈顶元素。
💡 典型题目
LeetCode 中的 栈 (Stack) 相关题目单纯就是对栈操作的细节考察,只需要将解题步骤编写为对应的代码即可。
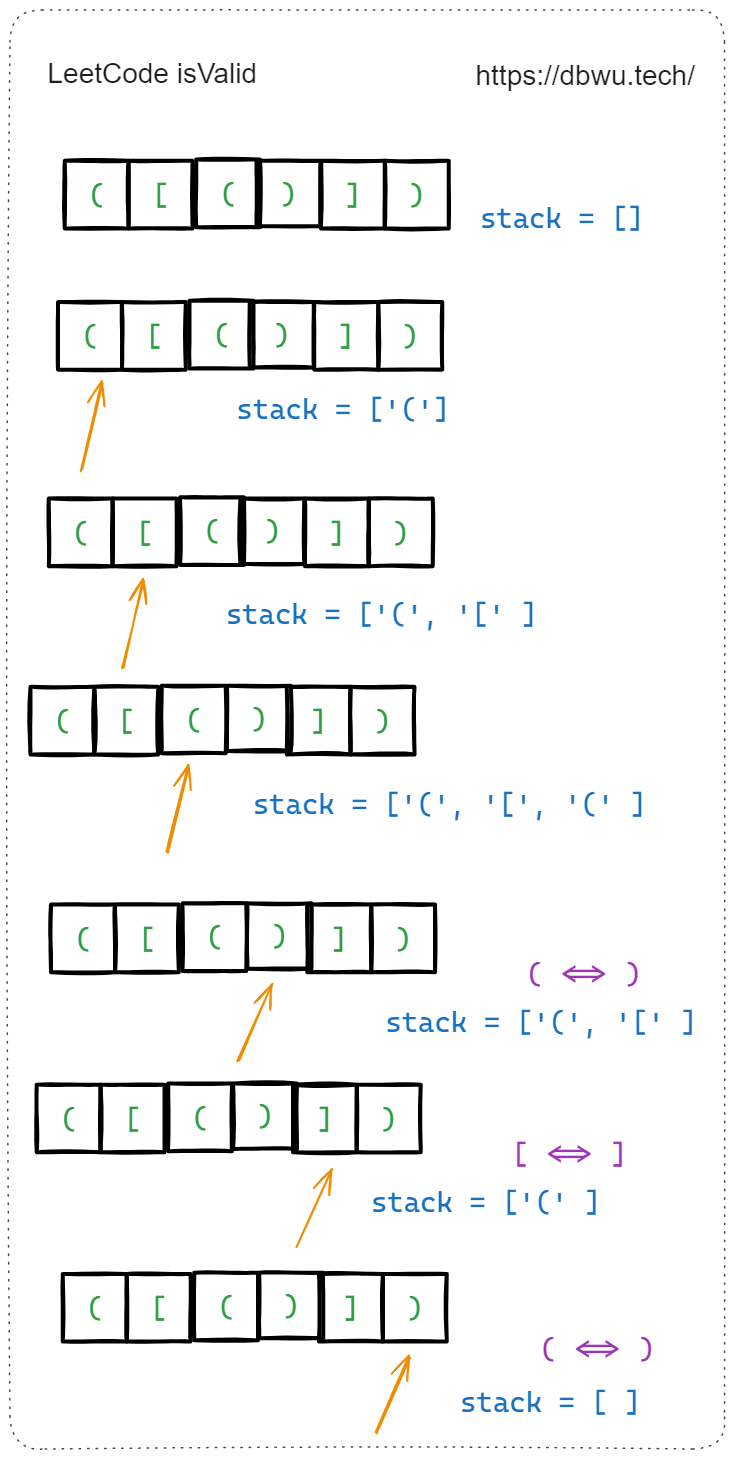
1. 有效的括号
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
# 示例来源: https://leetcode.cn/
示例 1:
输入:s = "()[]{}"
输出:true
示例 2:
输入:s = "(]"
输出:false
解题思路:
- 将字符分为两组,左边界组:
( { [, 右边界组) } ],并形成映射关系:( => ), { => }, [ => ] - 声明并初始化一个栈结构,用于存储字符
- 遍历字符串
- 如果当前字符属于左边界组,将其入栈
- 如果当前字符属于右边界组,取出栈顶字符
- 比较当前字符和栈顶字符是否为映射关系,如果不是,说明字符串不是有效括号,直接返回 false 即可
- 遍历字符串结束,确认栈是否为空,如果为空,说明字符串是有效括号,如果不为空,说明字符串不是有效括号
// 题解代码
func isValid(s string) bool {
// 如果 s 的长度为奇数,肯定不是有效括号
if len(s)&1 == 1 {
return false
}
// 将左右边界字符进行分组并形成映射
charMap := map[byte]byte{
'(': ')',
'{': '}',
'[': ']',
}
// 初始化栈
var stack []byte
for i := range s {
if _, ok := charMap[s[i]]; ok {
// 左边界组的字符直接入栈
stack = append(stack, s[i])
} else {
// 右边界组的字符与栈顶元素进行比较
index := len(stack) - 1
if len(stack) == 0 || s[i] != charMap[stack[index]] {
return false
}
stack = stack[:index]
}
}
// 此时栈内可能还存在一些左边界字符
// 所以需要判断栈是否为空
return len(stack) == 0
}
2.逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
# 示例来源: https://leetcode.cn/
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
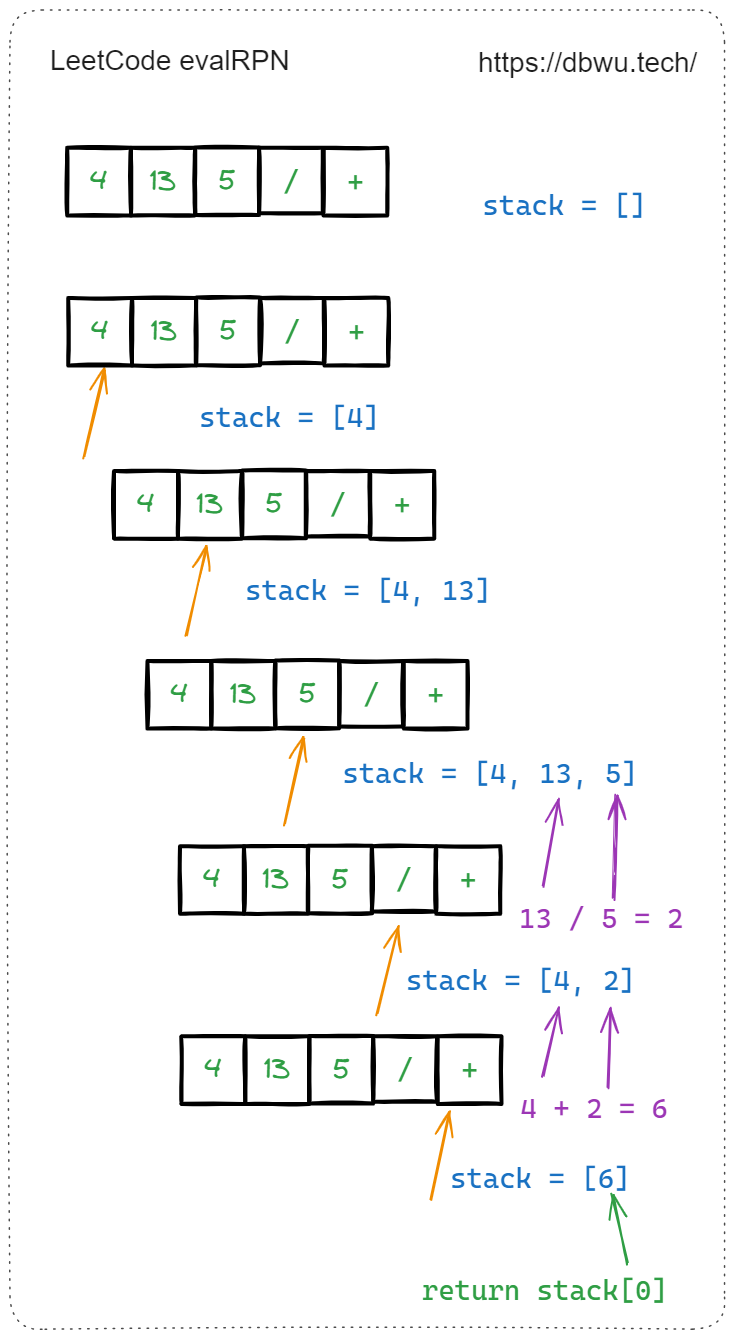
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
解题思路:
- 声明并初始化一个栈结构,用于存储遍历过程中遇到的数字
- 遍历 tokens 数组
- 如果当前 token 是数字,将其入栈
- 如果当前 token 是运算符,取出栈顶的两个数字,并根据运算符执行具体的计算,然后将计算结果加入栈
- 遍历 tokens 数组结束,返回栈底元素 (也就是最后一次计算出的结果值)
// 题解代码
func evalRPN(tokens []string) int {
if len(tokens) == 0 {
return 0
}
var stack []int
for _, token := range tokens {
// 将当前 token 解析为数字
val, err := strconv.Atoi(token)
// 如果没有发生错误
// 说明当前 token 为数字,直接入栈
if err == nil {
stack = append(stack, val)
} else {
// 说明当前 token 为运算符
// 取出栈顶的两个数字
num1, num2 := stack[len(stack)-2], stack[len(stack)-1]
stack = stack[:len(stack)-2]
// 根据不同的运算符执行不同的计算
// 同时将计算结果加入到栈中s
switch token {
case "+":
stack = append(stack, num1+num2)
case "-":
stack = append(stack, num1-num2)
case "*":
stack = append(stack, num1*num2)
case "/":
stack = append(stack, num1/num2)
}
}
}
// 返回栈底元素
return stack[0]
}
3. 简化路径
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为更加简洁的规范路径。
请注意,返回的 规范路径 必须遵循下述格式:
- 始终以斜杠 ‘/’ 开头。
- 两个目录名之间必须只有一个斜杠 ‘/’ 。
- 最后一个目录名(如果存在)不能 以 ‘/’ 结尾。
- 此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 ‘.’ 或 ‘..’)。
返回简化后得到的 规范路径 。
# 示例来源: https://leetcode.cn/
示例 1:
输入:path = "/home//foo/"
输出:"/home/foo"
解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
示例 2:
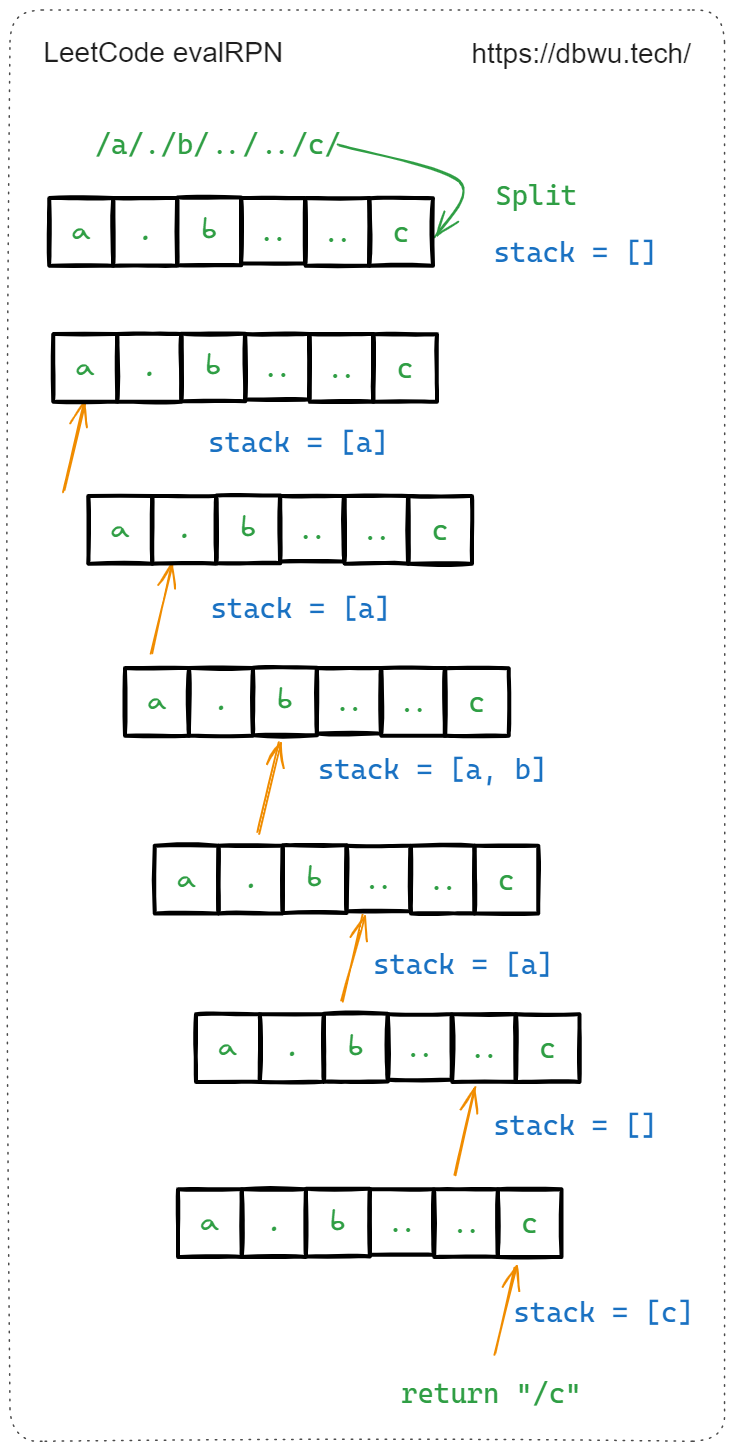
输入:path = "/a/./b/../../c/"
输出:"/c"
解题思路:
- 声明并初始化一个栈结构,用于存储遍历过程中遇到的 目录名称/文件名称
- 将参数路径使用
/分隔符分割为字符串数组 - 遍历字符串数组
- 如果当前字符串不是有效的路径字符,例如
""., 直接跳过 - 如果当前字符串是 目录名称/文件名称,将其入栈
- 如果当前字符串表示 上级目录
..,将栈顶元素出栈
- 如果当前字符串不是有效的路径字符,例如
- 遍历字符串数组结束,将栈内所有元素使用
/分隔符分割为字符串路径,然后在路径最前面加/即可
// 题解代码
func simplifyPath(path string) string {
var stack []string
for _, p := range strings.Split(path, "/") {
// 无效路径字符,直接跳过
if p == "" || p == "." {
continue
}
// 目录名称/文件名称 入栈
if p != ".." {
stack = append(stack, p)
} else if p == ".." && len(stack) > 0 {
// 如果是上级目录 ..
// 将栈顶元素出栈
stack = stack[:len(stack)-1]
}
}
return "/" + strings.Join(stack, "/")
}
📖 单调栈
单调栈(Monotonic Stack)是一种特殊的栈 (Stack) 结构,其元素满足特定的单调性条件,主要应用于 区间元素大小和顺序相关问题。
单调栈主要分为两种类型:
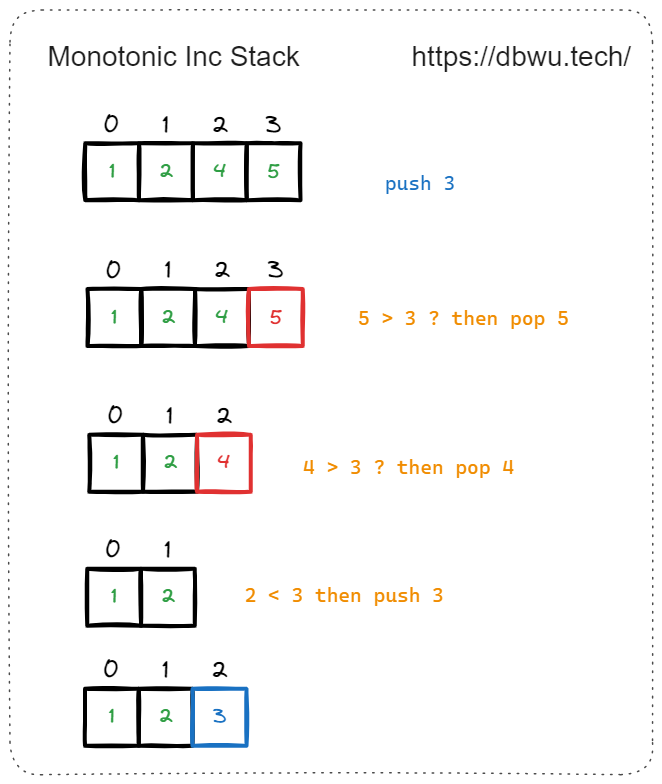
- 递增单调栈: 栈内元素从栈底到栈顶依次递增 (例如 1, 2, 3 …),当新元素入栈时,如果比栈顶元素大,直接入栈,否则循环弹出栈顶元素,直到满足单调递增的条件 (也即是找到比新元素小的栈顶元素,或者栈内元素为空),循环停止,然后将新元素入栈
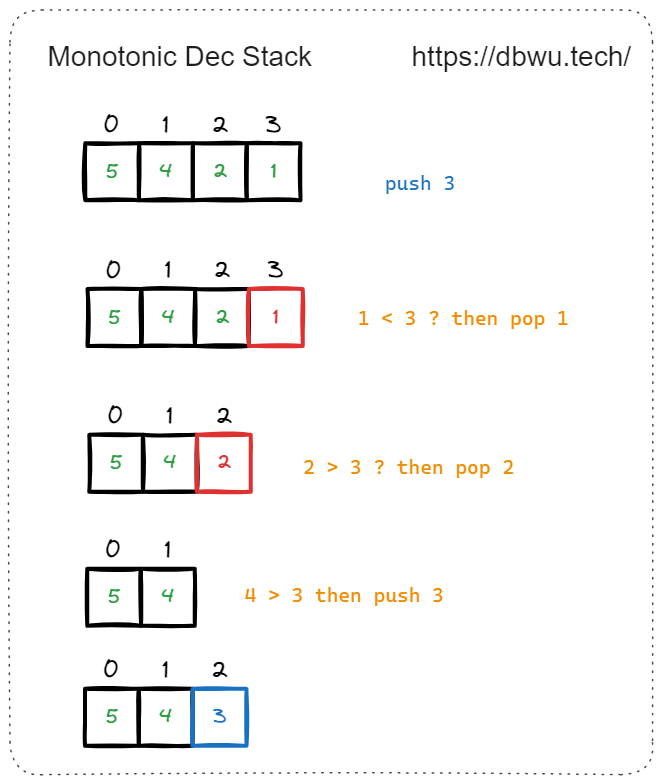
- 递减单调栈: 栈内元素从栈底到栈顶依次递减 (例如 3, 2, 1 …),当新元素入栈时,如果比栈顶元素小,直接入栈,否则循环弹出栈顶元素,直到满足单调递减的条件 (也即是找到比新元素大的栈顶元素,或者栈内元素为空),循环停止,然后将新元素入栈
LeetCode 模板
LeetCode 中单调栈相关题型解题时,可以采用如下步骤:
- 初始化一个栈数据结构,用于存储 元素的索引或值
- 遍历数组 (大多数 LeetCode 题目的输入数据是一个数组)
- 维护单调性:遍历过程中,将 元素的索引或值 按照单调性规则压入栈中,根据问题的具体逻辑,需要维护栈的单调递增性或单调递减性:
- 如果当前元素没有破坏栈的单调性,直接入栈即可
- 如果当前元素破坏了栈的单调性,弹出栈顶的元素,并 使用栈顶元素更新问题逻辑解或者做相应的处理
- 重复第 3 步,直到数组所有元素都已处理
- 根据题目要求确定是否处理栈中剩余元素
下面是一个通用的单调栈解题模板代码:
func Solution(nums []int) {
// 1. 初始化单调栈
stack := make([]int, 0)
// 2. 遍历数组
for i := range nums {
// 这里的示例为 单调递增栈
// 维护栈的单调性
for len(stack) > 0 && nums[i] < nums[stack[len(stack)-1]] {
// 获取栈顶元素
index := stack[len(stack)-1]
// 栈顶元素出栈
stack = stack[:len(stack)-1]
// 使用栈顶元素更新问题逻辑解或者做相应的处理
...
}
// 维护单调递增栈,将元素的索引入栈
stack = append(stack, i)
}
// 根据题目要求确定是否处理栈中剩余元素
for len(stack) > 0 {
...
}
}
💡 典型题目
1. 商品折扣
给你一个数组 prices ,其中 prices[i] 是商店里第 i 件商品的价格。
商店里正在进行促销活动,如果你要买第 i 件商品,那么你可以得到与 prices[j] 相等的折扣,其中 j 是满足 j > i 且 prices[j] <= prices[i] 的 最小下标 ,如果没有满足条件的 j ,你将没有任何折扣。
请你返回一个数组,数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。
# 示例来源: https://leetcode.cn/
示例 1:
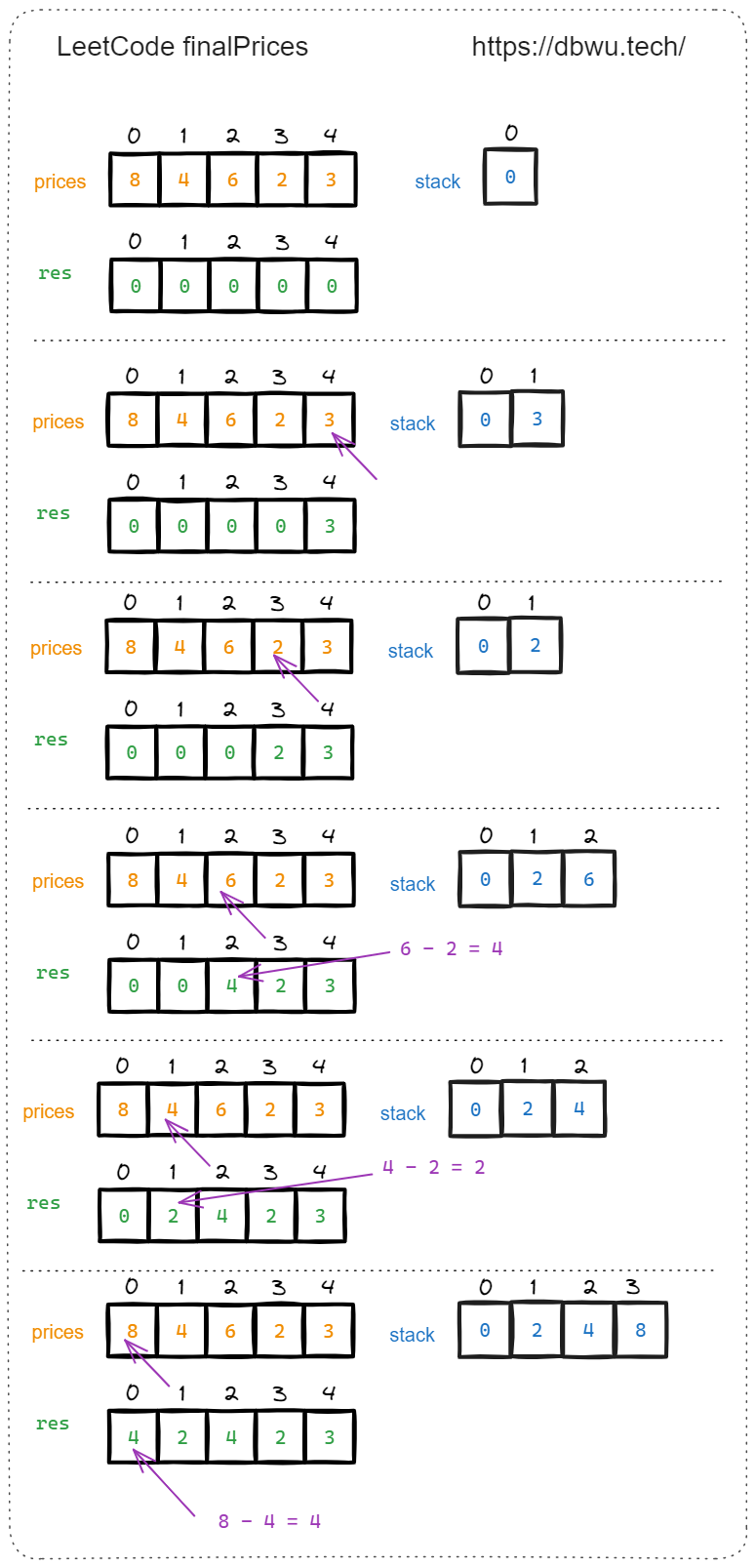
输入:prices = [8,4,6,2,3]
输出:[4,2,4,2,3]
解释:
商品 0 的价格为 price[0]=8 ,你将得到 prices[1]=4 的折扣,所以最终价格为 8 - 4 = 4 。
商品 1 的价格为 price[1]=4 ,你将得到 prices[3]=2 的折扣,所以最终价格为 4 - 2 = 2 。
商品 2 的价格为 price[2]=6 ,你将得到 prices[3]=2 的折扣,所以最终价格为 6 - 2 = 4 。
商品 3 和 4 都没有折扣。
示例 2:
输入:prices = [1,2,3,4,5]
输出:[1,2,3,4,5]
解释:在这个例子中,所有商品都没有折扣。
直接将单调栈解题模板代码稍微修改后即可,为了便于阅读,直接将解题和思路以注释的方式写入到代码中。
// 题解代码
func finalPrices(prices []int) []int {
n := len(prices)
res := make([]int, n)
// 1. 初始化单调栈
// 因为只需要计算折扣后的值
// 所以栈内存储数组值就可以
// 栈顶始终保留一个值 0 作为 “哨兵”
// 避免边界检查,同时表示语义: “没有折扣”
stack := []int{0}
// 2. 遍历数组
// 题目声明,享受折扣时的索引必须比当前索引大
// 也就是说,数组中的最后一件商品价格无法享受任何优惠
// 所以数组从后向前遍历即可
for i := n - 1; i >= 0; i-- {
// 当前栈内的商品价格依次递增,符合单调递增的特性
// 也就是说,如果一个商品价格出现在栈内
// 说明还未找到 该商品价格 对应的 折扣价格
// 3. 维护单调递增性
// 如果 栈顶商品价格 比 当前商品价格 大,说明当前单调递增性已经被破坏
// 那么此时就可以开始给当前商品 寻找对应的 折扣价格 了
// 弹出栈顶商品价格,直到遇到比 当前商品价格 小的 商品价格(折扣价格)
for len(stack) > 1 && stack[len(stack)-1] > prices[i] {
stack = stack[:len(stack)-1]
}
// 4. 处理具体逻辑
// 此时 栈顶商品价格 就是 当前商品价格 可以享受的折扣
// 更新即可
res[i] = prices[i] - stack[len(stack)-1]
// 将当前商品价格入栈
stack = append(stack, prices[i])
}
return res
}
2. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
# 示例来源: https://leetcode.cn/
示例 1:
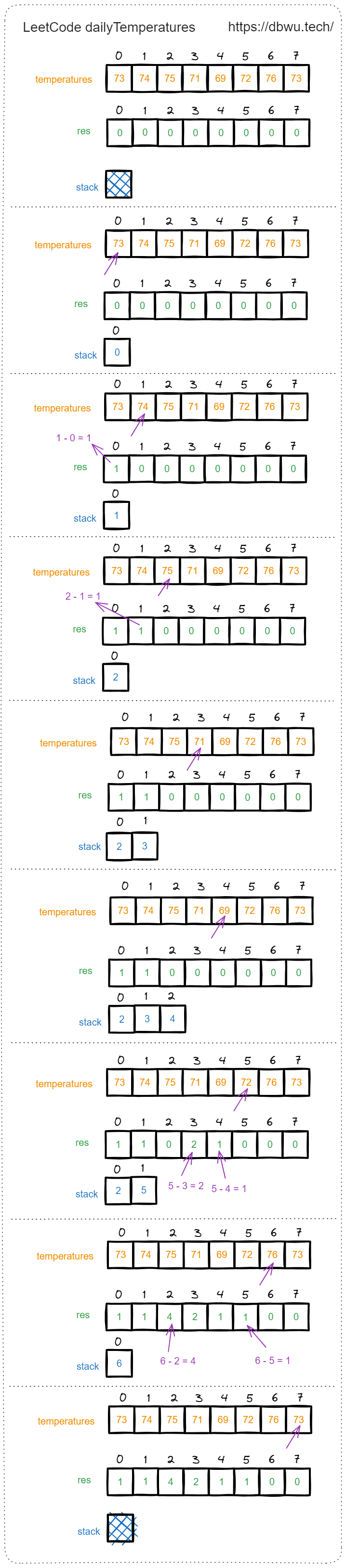
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
直接将单调栈解题模板代码稍微修改后即可,为了便于阅读,直接将解题和思路以注释的方式写入到代码中。
// 题解代码
func dailyTemperatures(temperatures []int) []int {
res := make([]int, len(temperatures))
// 1. 初始化单调栈
// 因为题目要求寻找 “下一个” 更高的温度对应的索引 (间隔天数)
// 所以栈内存储数组索引
var stack []int
// 2. 遍历数组
for i := range temperatures {
// 当前栈内索引对应的温度依次递减,符合单调递减的特性
// 也就是说,如果一个索引出现在栈内
// 说明还未找到该索引对应的温度 的 “下一个” 更高的温度
// 3. 维护单调递减性
// 如果当前元素温度 大于 栈顶元素温度
// 说明当前单调递减性已经被破坏
// 那么当前元素就是 “下一个” 更高的温度
for len(stack) > 0 && temperatures[i] > temperatures[stack[len(stack)-1]] {
// 4. 处理具体逻辑
// 获取栈顶元素索引
preIndex := stack[len(stack)-1]
// 栈顶元素出栈
stack = stack[:len(stack)-1]
// 更新栈顶元素索引对应的温度 的 “下一个” 更高的温度
// 因为题目要求寻找 “下一个” 更高的温度在几天后
// 所以这里使用当前索引 减去 栈顶索引
// 得出的差值就是中间的间隔天数
res[preIndex] = i - preIndex
}
// 将当前元素的索引入栈
stack = append(stack, i)
}
return res
}
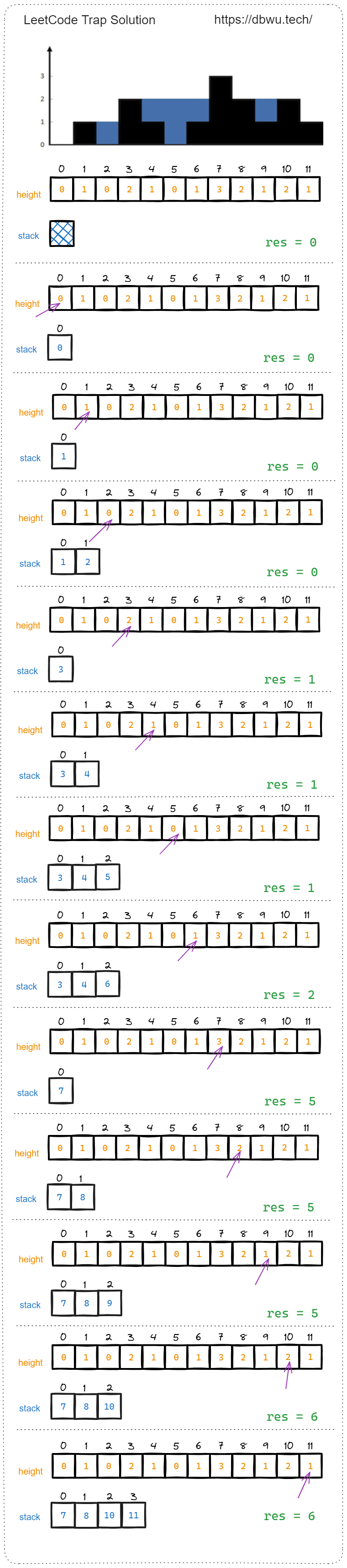
3. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
直接将单调栈解题模板代码稍微修改后即可,为了便于阅读,直接将解题和思路以注释的方式写入到代码中。
// 题解代码
func trap2(height []int) int {
res := 0
// 1. 初始化单调栈
// 栈内存储数组索引
var stack []int
// 2. 遍历数组
for i := range height {
// 当前栈内索引对应的柱子依次递减,然后寻找右侧 “更高的柱子” 用来蓄水
// 符合单调递减的特性
// 也就是说,如果一个索引出现在栈内
// 说明还未找到该索引对应的柱子 的右侧 “更高的柱子”
// 3. 维护单调递减性
// 如果当前柱子高度 大于 栈顶元素高度
// 说明当前单调递减性已经被破坏
// 那么当前元素就是 右侧 “更高的柱子”
for len(stack) > 0 && height[i] > height[stack[len(stack)-1]] {
// 4. 处理具体逻辑
// 获取栈顶元素索引
top := stack[len(stack)-1]
// 栈顶元素出栈
stack = stack[:len(stack)-1]
// 如果栈内只有一个元素
// 那么此时 stack 的长度等于 0
// 也就说明此时才刚刚找到 “左边的柱子”
// 还没有找到 “右边的柱子”
// 比如这种情况 [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]
// 当 i 为 1 时,左边的柱子 (栈顶元素) 是 0
// 这时接不到任何雨水,所以无需计算
if len(stack) > 0 {
left := stack[len(stack)-1]
// 左右两个柱子之间的距离
w := i - left - 1
// 左右两个柱子之间的高度,以较低的为准,“木桶原理”
h := min(height[i], height[left]) - height[top]
// 将左右两个柱子之间的面积 (也就是蓄水容量) 累积到总计值
res += w * h
}
}
stack = append(stack, i)
}
return res
}