LeetCode 拓扑排序 刷题模板
📖 概述
拓扑排序是一种对有向无环图(DAG)进行排序的算法,可以将图中的节点 (顶点) 按照一种线性顺序进行排列,其中每个节点 v 仅在其所有依赖关系都被访问后才被访问。
拓扑排序的典型应用是根据作业或任务的依赖性来调度作业或任务序列,作业由顶点表示,如果作业 x 必须在作业 y 开始之前完成,则从 x 到 y 存在一条边(例如,洗衣服时,洗衣机必须在我们将衣服放入烘干机之前完成)。
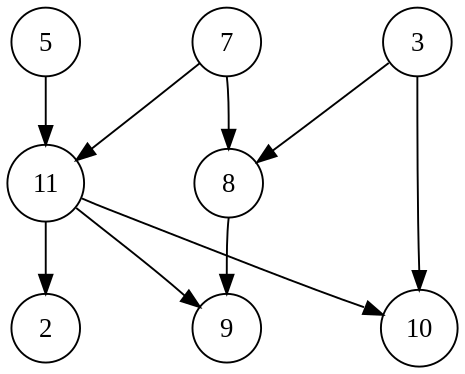
上面是一个典型的图结构,该图包含很多有效的拓扑排序,如果我们尝试从上到下,从左到右的顺序,可以得到如下的拓扑排序结果: 5、7、11、2、3、8、9、10。
算法步骤
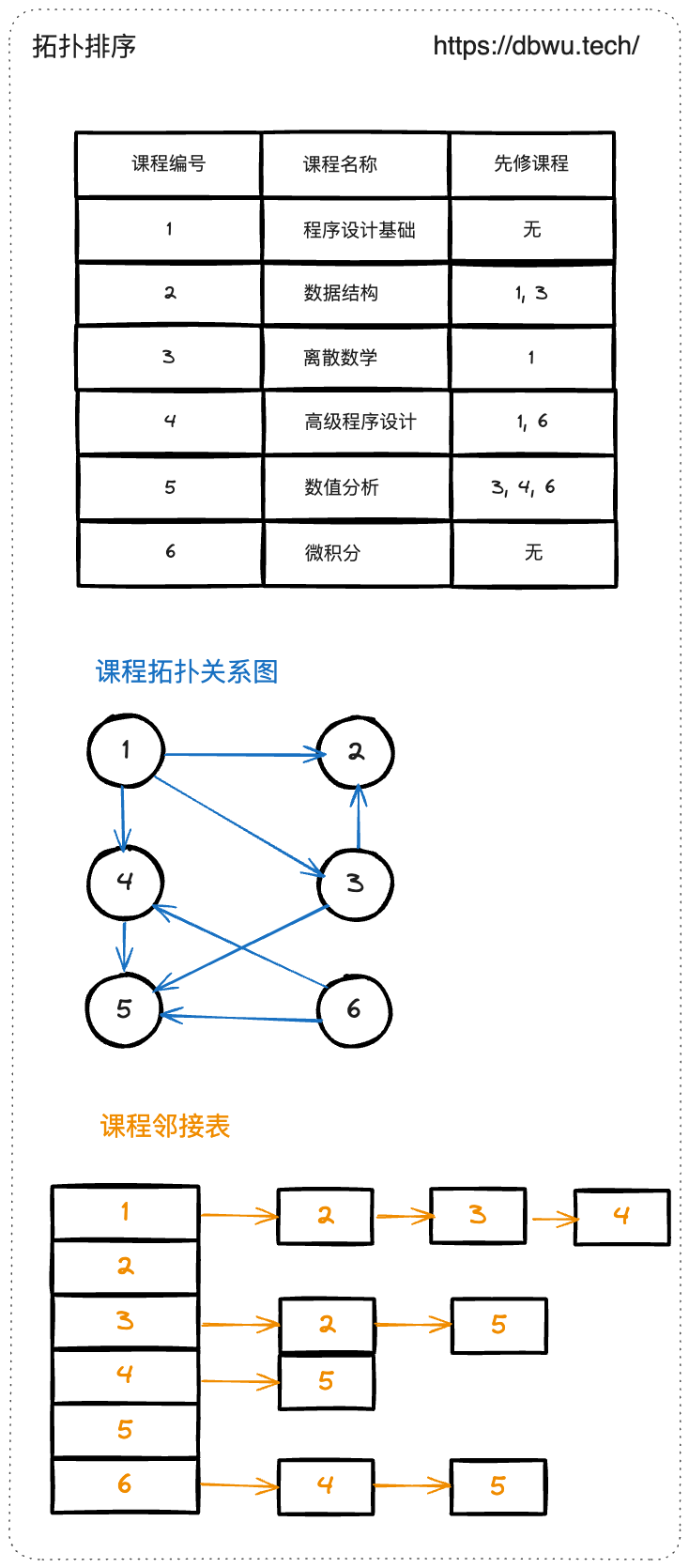
拓扑排序的基本算法思想是: 通过不断删除入度为 0 的节点,并更新其相邻节点的入度,直到所有节点都访问过结束。所谓入度为 0 的节点是指在有向图中,没有任何边指向该节点的节点,也就是说,该及节点没有任何 “前置节点”,可以直接访问,因此入度为 0 的节点就是拓扑排序的起点。
下面的图结构中,节点 5, 节点 7, 节点 3 都是入度为 0 的节点。

下面是拓扑排序的一般步骤:
- 将拓扑约束 (前置) 条件转换为邻接表
- 初始化一个队列,将图中所有入度为 0 的节点加入队列
- 循环从队列中取出节点,然后加入到拓扑排序结果中
- 对于每个取出的节点,遍历其相邻节点,并将相邻节点的入度减去 1, 如果相邻节点的入度减去 1 之后入度变为 0, 则将其加入到队列
- 重复步骤 2 和 3, 直到队列为空
LeetCode 刷题模板
笔者根据 LeetCode 中的拓扑排序相关算法题,整理了一个通用刷题模板。
func Solution(prerequisites [][]int) []int {
// 初始化入度数组和邻接表
inDegree := make([]int, n)
graph := make(map[int][]int)
// 将拓扑约束条件转换为邻接表
for _, prerequisite := range prerequisites {
course, prerequisite := prerequisite[0], prerequisite[1]
graph[prerequisite] = append(graph[prerequisite], course)
inDegree[course]++
}
// 初始化队列
// 将图中所有入度为 0 的节点加入队列
queue := make([]int, 0)
for i := 0; i < n; i++ {
if inDegree[i] == 0 {
queue = append(queue, i)
}
}
// 初始化结果集
result := make([]int, 0)
// 进行拓扑排序
for len(queue) > 0 {
node := queue[0]
queue = queue[1:]
// 从队列中取出节点,然后加入到拓扑排序结果中
result = append(result, node)
// 遍历节点的相邻节点
for _, neighbor := range graph[node] {
// 将相邻节点的入度减去 1
inDegree[neighbor]--
// 如果相邻节点的入度减去 1 之后入度变为 0, 则将其加入到队列
if inDegree[neighbor] == 0 {
queue = append(queue, neighbor)
}
}
}
// 判断是否存在环
// 存在环,无法完成拓扑排序
...
return result
}
通过上面的模板代码可以看到,拓扑排序的实现基础就是之前的文章中写过的 广度优先搜索 (BFS) 算法。
💡 典型题目 (图)
1. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
# 示例来自: https://leetcode.cn/
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
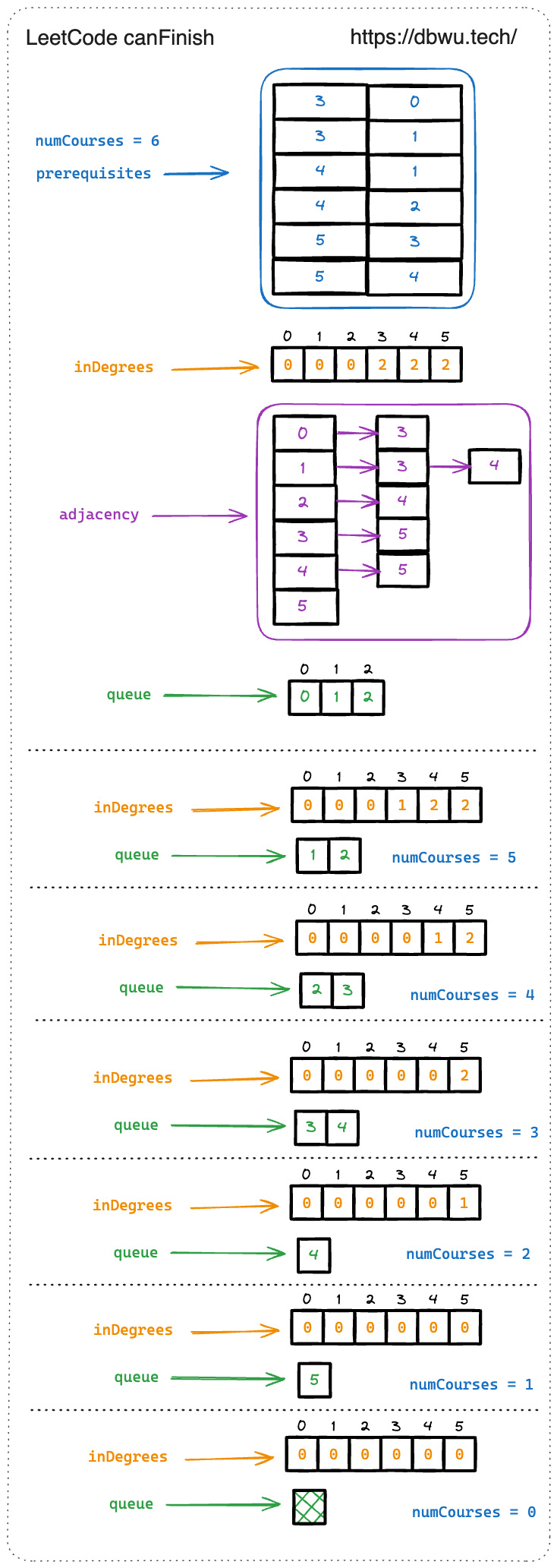
直接在拓扑排序代码模板的基础之上修改即可,为了节省篇幅和增强代码可读性,解题思路全部写在了代码中。
// 题解代码
func canFinish(numCourses int, prerequisites [][]int) bool {
// 使用 数组 表示每个课程作为其他课程的前置数量总和
// 例如 课程 2, 3, 4 的前置课程都是课程 1, 表示为 inDegrees[1] = 3
inDegrees := make([]int, numCourses)
// 使用 邻接表 表示课程之间的前置拓扑关系矩阵
adjacency := make([][]int, numCourses)
// 初始化邻接表内部的的二维数组
for i := 0; i < numCourses; i++ {
adjacency[i] = []int{}
}
// 计算课程的前置数量和邻接表关系矩阵
for _, v := range prerequisites {
inDegrees[v[0]]++
adjacency[v[1]] = append(adjacency[v[1]], v[0])
}
// 如果课程的前置课程数量为 0
// 说明该课程可以直接学习,加入 BFS 队列
var queue []int
for i := 0; i < numCourses; i++ {
if inDegrees[i] == 0 {
queue = append(queue, i)
}
}
// BFS 搜索
for len(queue) > 0 {
pre := queue[0]
queue = queue[1:]
// 当前课程的前置课程数量为 0, 可以直接学习
// 将需要学习的课程总数量 - 1
numCourses--
// 从当前课程开始,进行 BFS 搜索将其作为前缀的课程的 后缀课程
for _, cur := range adjacency[pre] {
// 学完了当前课程,后缀课程数量 - 1
inDegrees[cur]--
// 如果后缀课程的前置课程数量为 0
// 说明该课程可以直接学习,加入 BFS 队列
if inDegrees[cur] == 0 {
queue = append(queue, cur)
}
}
}
// 如果已经学习完课程,那么此时课程总数量应该等于 0
// 因为每学习一门前置课程数量为 0 的课程后
// 都要将学习的课程总数量 - 1
return numCourses == 0
}
2. 课程表 II
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。 返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
# 示例来自: https://leetcode.cn/
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
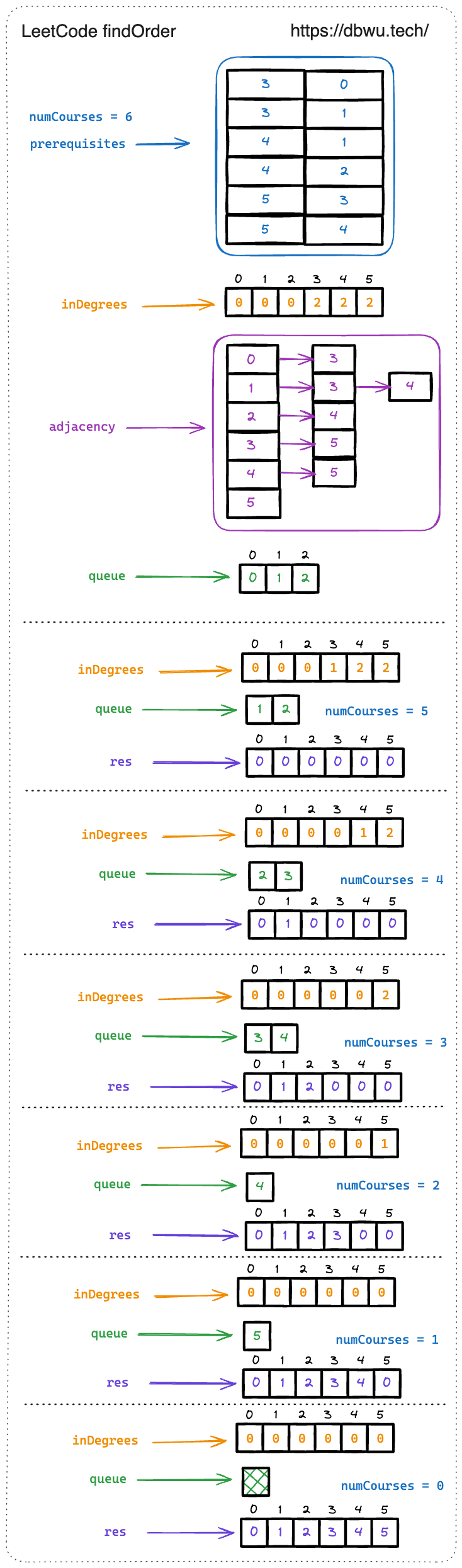
直接在上一题的基础上略加修改即可: 每次从队列中取出入度为 0 的节点时,添加到返回结果集中。
// 题解代码
func findOrder(numCourses int, prerequisites [][]int) []int {
// 使用 数组 表示每个课程作为其他课程的前置数量总和
// 例如 课程 2, 3, 4 的前置课程都是课程 1, 表示为 inDegrees[1] = 3
inDegrees := make([]int, numCourses)
// 使用 邻接表 表示课程之间的前置拓扑关系矩阵
adjacency := make([][]int, numCourses)
// 初始化邻接表内部的的二维数组
for i := 0; i < numCourses; i++ {
adjacency[i] = []int{}
}
// 计算课程的前置数量和邻接表关系矩阵
for _, v := range prerequisites {
inDegrees[v[0]]++
adjacency[v[1]] = append(adjacency[v[1]], v[0])
}
// 如果课程的前置课程数量为 0
// 说明该课程可以直接学习,加入 BFS 队列
var queue []int
for i := 0; i < numCourses; i++ {
if inDegrees[i] == 0 {
queue = append(queue, i)
}
}
// 记录课程学习顺序
res := make([]int, numCourses)
// 记录课程学习顺序的位置索引
pos := 0
// BFS 搜索
for len(queue) > 0 {
pre := queue[0]
queue = queue[1:]
// 更新课程学习顺序
res[pos] = pre
// 更新索引
pos++
for _, cur := range adjacency[pre] {
// 学完了当前课程,后缀课程数量 - 1
inDegrees[cur]--
// 如果后缀课程的前置课程数量为 0
// 说明该课程可以直接学习,加入 BFS 队列
if inDegrees[cur] == 0 {
queue = append(queue, cur)
}
}
}
// 可以学习完所有课程
if pos == numCourses {
return res
}
return []int{}
}