字节序概述
2023-02-20 计算机基础
字节序
字节序: 多字节数据在内存中的排列顺序。
大端序和小端序
大端序: 高位字节在左边,低位字节在右边。
// a = 0x12345678
// 大端序表示,符合人类阅读习惯
// -----------------------------
// | 0x12 | 0x34 | 0x56 | 0x78 |
// -----------------------------
// 低地址 <---------------> 高地址
小端序: 低位字节在左边,高位字节在右边。
在计算机内部,
小端序被广泛应用于现代性 CPU 内部存储数据。
// a = 0x12345678
// 小端序表示
// -----------------------------
// | 0x78 | 0x56 | 0x34 | 0x12 |
// -----------------------------
// 低地址 <---------------> 高地址
大端序优势
检查正负位
// a = 123456
//
// -------------------------
// 小端序表示 | 5 | 4 | 3 | 2 | 1 | - |
// -------------------------
// -------------------------
// 大端序表示 | - | 1 | 2 | 3 | 4 | 5 |
// -------------------------
// 低地址 <------------> 高地址
大端序 只需要读取第 1 位,就可以确定正负,大端序 需要读取到最后 1 位,才可以确定正负。
小端序优势
检查奇偶性
// a = 123456
//
// -------------------------
// 小端序表示 | 6 | 5 | 4 | 3 | 2 | 1 |
// -------------------------
// -------------------------
// 大端序表示 | 1 | 2 | 3 | 4 | 5 | 6 |
// -------------------------
// 低地址 <------------> 高地址
小端序 只需要读取第 1 位,就可以确定奇偶,大端序 需要读取到最后 1 位,才可以确定奇偶。
比较大小
比较 3 个数字的大小: 1, 234, 56789
// 小端序表示
// ---------------------
// | 9 | 8 | 7 | 6 | 5 |
// | 4 | 3 | 2 | | |
// | 1 | | | | |
// ---------------------
// 低地址 <--------> 高地址
// 大端序表示
// ---------------------
// | 5 | 6 | 7 | 8 | 9 |
// | | | 2 | 3 | 4 |
// | | | | | 1 |
// ---------------------
// 低地址 <--------> 高地址
小端序 只需要从左到右读取,哪个数字读取不到下一位,就可以确定是最小的数字,大端序 需要读取到最后 1 位,才可以确定最小数字。
小端序 在极端情况下 (所有数字位数相同),和大端序一样,需要读取到最后 1 位。
乘法
计算 24165 * 3841
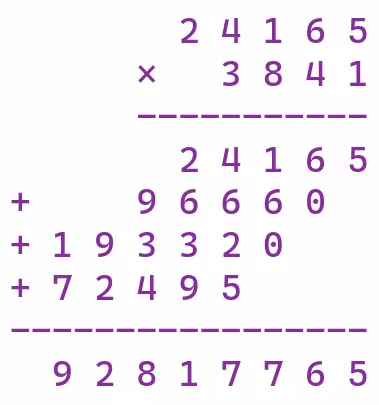
上图是 大端序 的 24165 乘以 3841,大端序 的乘法是向左进位,也就是向左边扩展,必须等到每一轮的结果都出来(上例是四轮),再相加统一写入内存。

上图是 小端序 的 24165 乘以 3841,小端序 的乘法是向右进位,也就是向右边扩展,左边的边界不变。每一轮结果写入内存后,就不需要移动,后面有变化只需要改动对应的位就行了。
任意精度整数
任意精度整数又称 大整数,可以存放任意大小的整数。它的内部实现是把整数分成一个个较小的单位,通常是 uint32(无符号32位整数)或 uint64(无符号64位整数),按顺序组合在一起。
// 大整数内部表示
// -------------------------------------
// | uint64 | uint64 | uint64 | uint64 |
// -------------------------------------
大端序 表示的情况下,第一个 uint64 就是这个整数最大的部分,运算时,一旦这个数发生变化,需要进位,后面的所有位都必须移动和改写。
小端序 表示的情况下,发生进位时,不需要所有位移动,所以比 大端序 更快。
小端序 的另一个好处是,如果逐字节的运算从个位数开始(比如乘法和加法),可以从左到右依次运算一个个 uint64,算完上一个再读取下一个。
大端序 就不行,必须读取整个数以后再进行运算。
更改数据类型
C 语言有一种 cast 操作,可以强制改变变量的数据类型,比如把 32 位整数强行改变为 16 位整数。

上图中,32 位整数 0x00000001 更改为 16 位整数 0x0001,大端序 是截去前面两个字节,这时指向这个地址的指针必须向后移动两个字节。
小端序 就没有这个问题,截去的是后面两个字节,第一位的地址是不变的,所以指针不需要移动。
总结
如果需要逐位运算,或者需要到从个位数开始运算,都是 小端序 占优势。反之,如果运算只涉及到高位,或者数据的可读性比较重要,则是 大端序 占优势。
转载声明
本文转载自 字节序探析:大端与小端的比较,笔者在文字描述和图片排版上略作修改。
补充
Go 语言标准库中的 encoding/binary 包实现了数字和字节序列之间的简单转换以及编码解码。
package binary
// Read 将结构化二进制数据读取到 data
func Read(r io.Reader, order ByteOrder, data any) error {}
// Write 将结构化二进制数据写入到 w
func Write(w io.Writer, order ByteOrder, data any) error {}
...
Read 示例代码
package main
import (
"bytes"
"encoding/binary"
"fmt"
)
func main() {
var pi float64
b := []byte{0x18, 0x2d, 0x44, 0x54, 0xfb, 0x21, 0x09, 0x40}
buf := bytes.NewReader(b)
err := binary.Read(buf, binary.LittleEndian, &pi)
if err != nil {
fmt.Println("binary.Read failed:", err)
}
fmt.Println(pi)
}
// $ go run main.go
// 3.141592653589793
Write 示例代码
package main
import (
"bytes"
"encoding/binary"
"fmt"
"math"
)
func main() {
buf := new(bytes.Buffer)
var pi = math.Pi
err := binary.Write(buf, binary.LittleEndian, pi)
if err != nil {
fmt.Println("binary.Write failed:", err)
}
fmt.Printf("% x\n", buf.Bytes())
}
// $ go run main.go
// 18 2d 44 54 fb 21 09 40
