LeetCode 双指针 刷题模板
概述
双指针,顾名思义,就是使用两个指针来解决算法题。LeetCode 中的双指针类型题目属于比较基础的算法题,一般是简单难度,少部分是中等难度,通常出现在数组、字符串、链表相关题目中。双指针类型的题目一般都会要求在 数组/字符串等 参数上面原地移动/变换,所以不能使用额外的空间来解题。双指针属于高频笔试题,尤其是快慢指针、左右指针两种类型,必须熟练掌握。
类型和命名建议
合理的命名方式可以提高代码可读性,解决算法题的同时还可以将思路直观地展示出来。
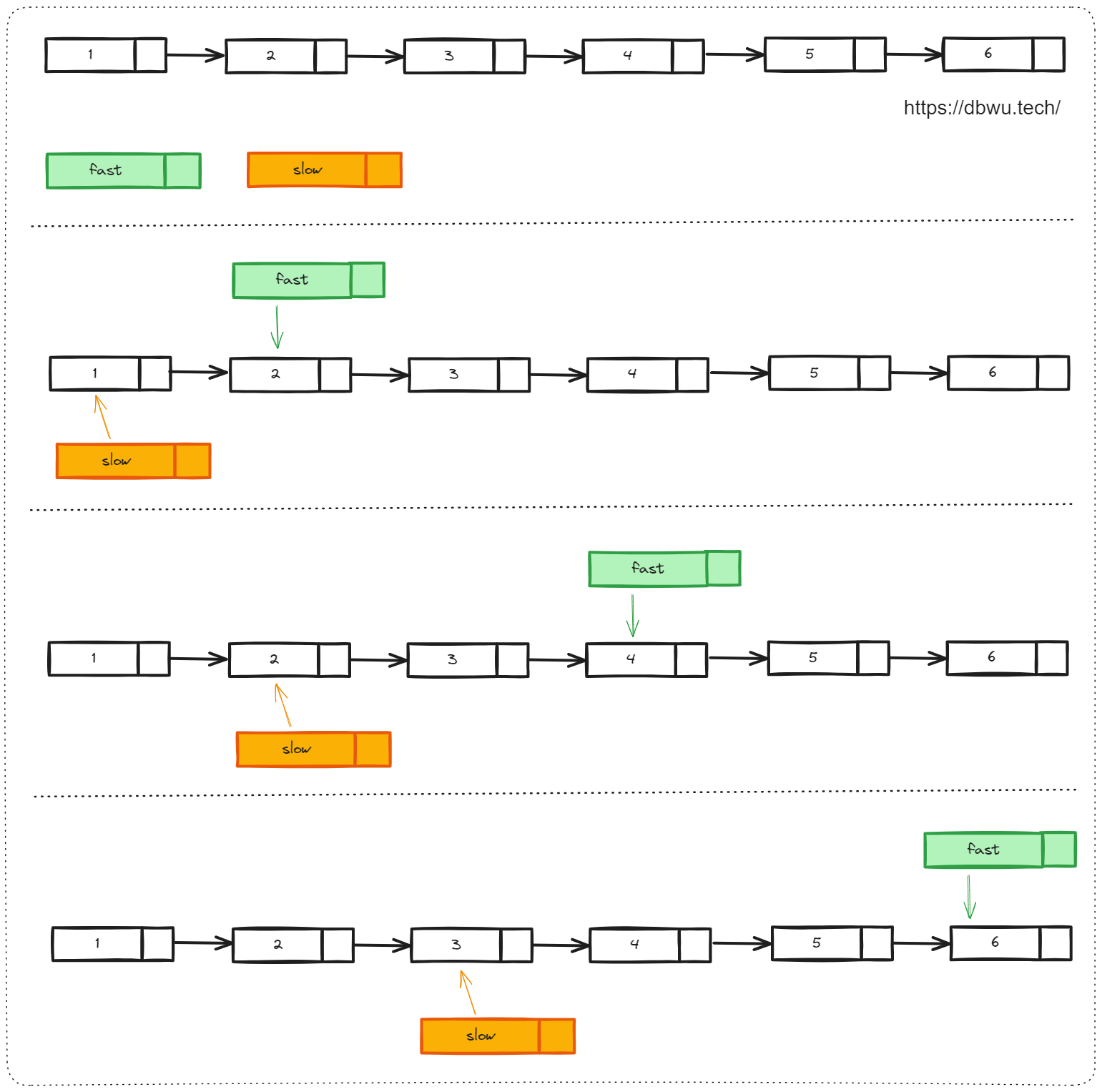
1. 快慢指针
最经典的双指针使用场景,例如 之前这篇文章 中,使用快慢指针模板快速优雅解决链表相关算法题。
一般情况下,快慢指针的固定命名:
快指针: fast
慢指针: slow
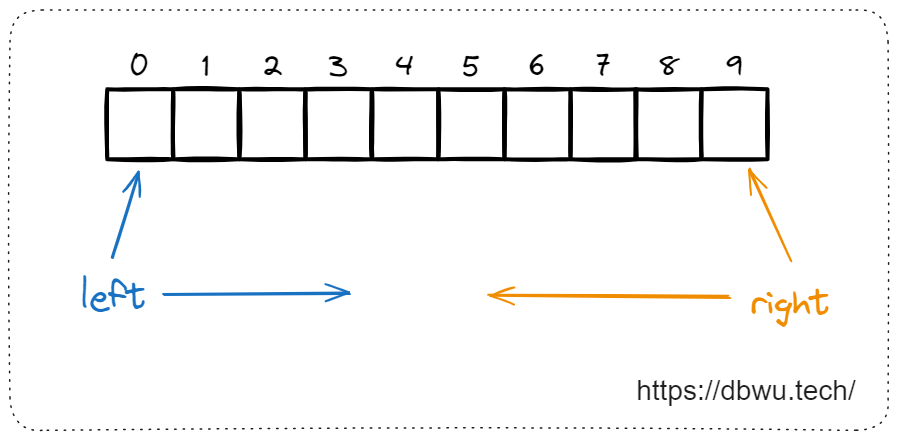
2. 左右指针
通常用于解决数组或字符串问题,其中:
- 左指针通常指向数组下标 0 ,字符串的开始位置
- 右指针通常指向数组下标 N-1 (其中 N 为数组长度),字符串的结束位置
一般情况下,左右指针的固定命名:
左指针: left
右指针: right
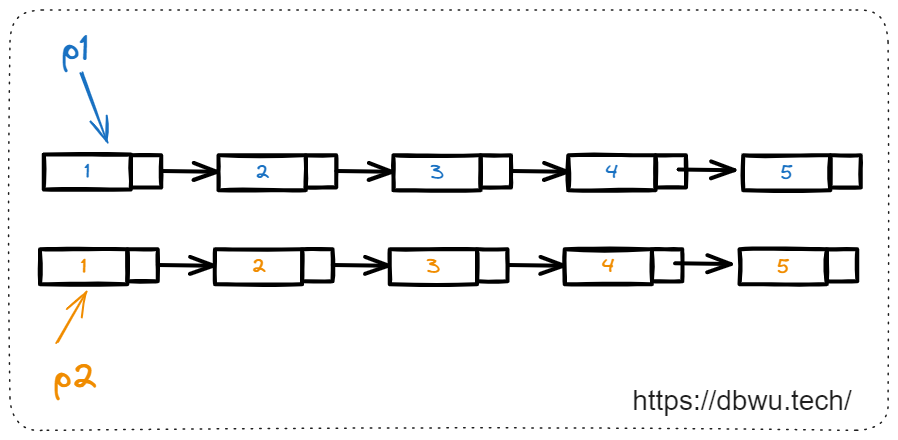
3. 无序指针
如果两个指针没有任何语义和逻辑顺序,只是用于指向不同的地址,也可以直接简单命名。
例如在 合并两个有序链表 这道题中,可以使用两个无序指针分别指向链表 1 和链表 2:
指针 1: p1
指针 2: p2
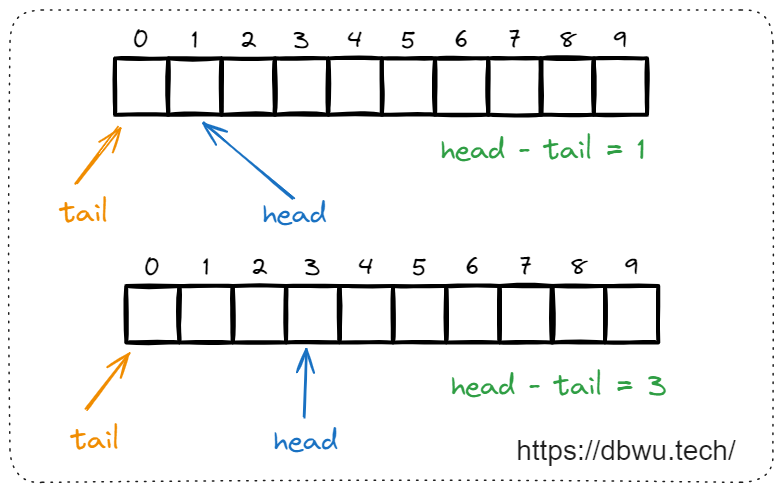
4. 头尾指针
这种场景中,两个指针每次移动的位置不一样,可能移动也可能原地不动 (所以单纯应用角度分析的话,头尾双指针 属于 快慢双指针的子集),例如使用数组使用的环形队列数据结构。
一般情况下,头尾指针的固定命名:
头指针 1: head
尾指针 2: tail
常见错误
下面列举使用双指针解题过程中常见的错误和 Bug 原因。
移动错误
常见的错误包括:
- 数组/字符串指针索引访问越界、边界判断未处理
- 数组/字符串指针索引移动方向错误
- 数组/字符串指针索引步长增长错误
指针初始化问题
- 链表指针未初始化指向,直接访问错误
- 空数组/空字符串直接访问越界
死循环
- 快慢指针的终止条件设置错误
- 循环队列的终止条件设置错误
滑动窗口
对于滑动窗口类型的题目,通常使用两个指针维护窗口的左右边界,然后根据题目要求移动窗口。需要注意的是,窗口的大小可能会变化,因此要准备调整窗口的大小和位置。
💡 快慢双指针
快慢双指针的经典使用场景在 之前这篇文章 中已经做过讲解,本文不再赘述。
💡 头尾双指针
头尾双指针的典型使用场景是:
- 头指针 作为数组/字符串的遍历索引,从起始位置遍历到结束位置
- 尾指针 作为条件指针,每次移动 0 个位置或 1 个位置,并在满足题目逻辑条件时更新返回值,或者自身作为最终返回值
// 模板代码
func Solution(nums []int) int {
tail := 0
for head := range nums {
// do something
...
}
return tail
}
此外可以根据参数快速进行边界类检测,比如数组元素去重类问题,可以先看数组长度,少于 2 时直接返回参数的数组长度:
if len(nums) < 2 {
return len(nums)
}
再比如字符串的匹配类问题,如果子字符串长度比匹配字符串长度还要长,直接返回 -1:
if len(source) < len(target) {
return -1
}
1. 原地删除元素
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
# 示例来自: https://leetcode.cn/
# 示例 - 1
输入:nums = [1,1,2]
输出:2, nums = [1,2]
# 示例 - 2
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
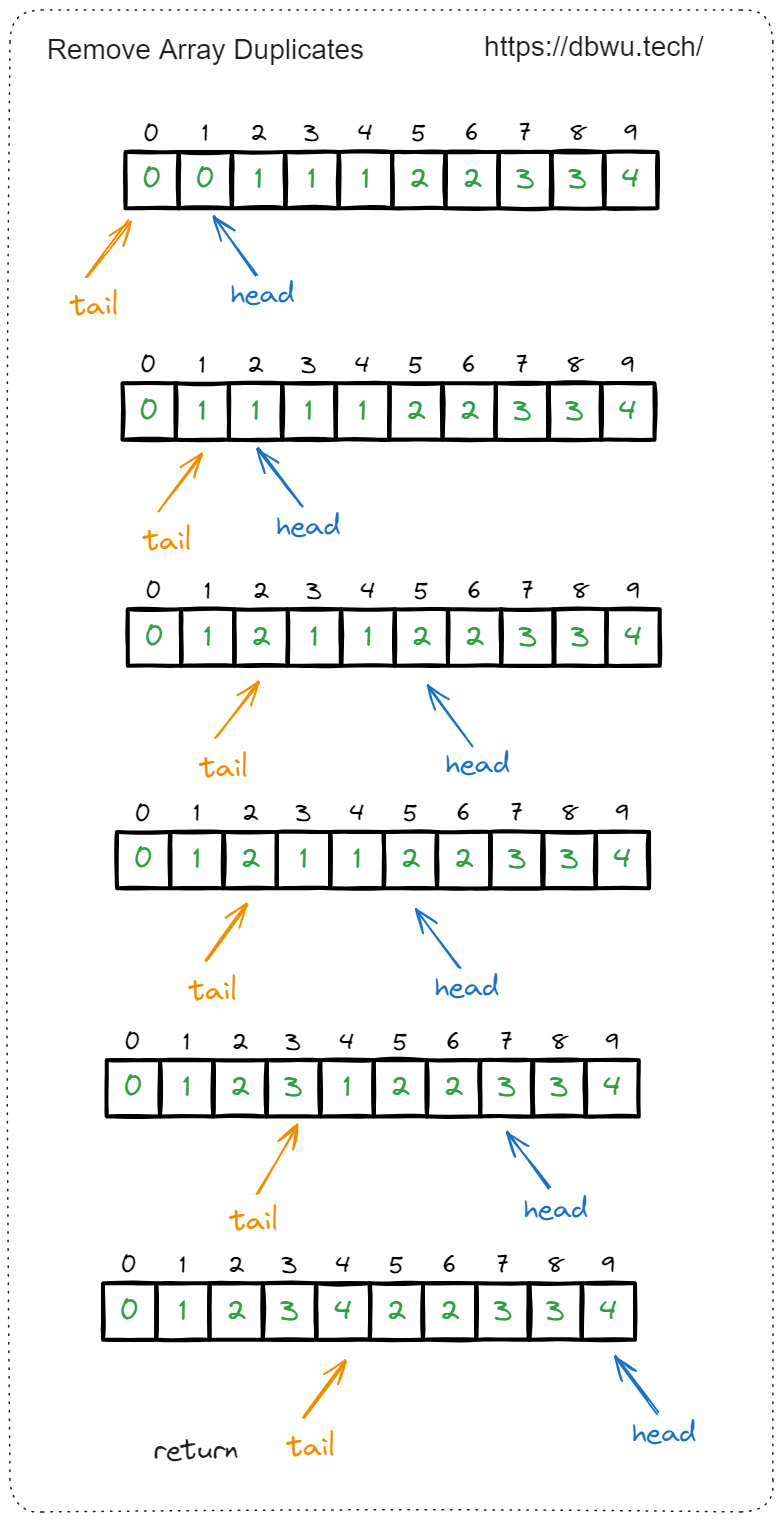
快速套模板:
- 定义头指针为 head, 尾指针为 tail
- head 作为遍历数组索引,但是下标从 1 开始 (因为下标为 0 的元素有可能就是重复的)
- tail 作为更新元素去重的索引
- 最终返回 tail 指针 (tail + 1 表示去重之后的新数组长度, 因为数组的下标从 0 开始)
// 题解代码
func removeDuplicates(nums []int) int {
tail := 0
for head := 1; head < len(nums); head++ {
if nums[head] != nums[tail] {
tail++
nums[tail] = nums[head]
}
}
return tail + 1
}
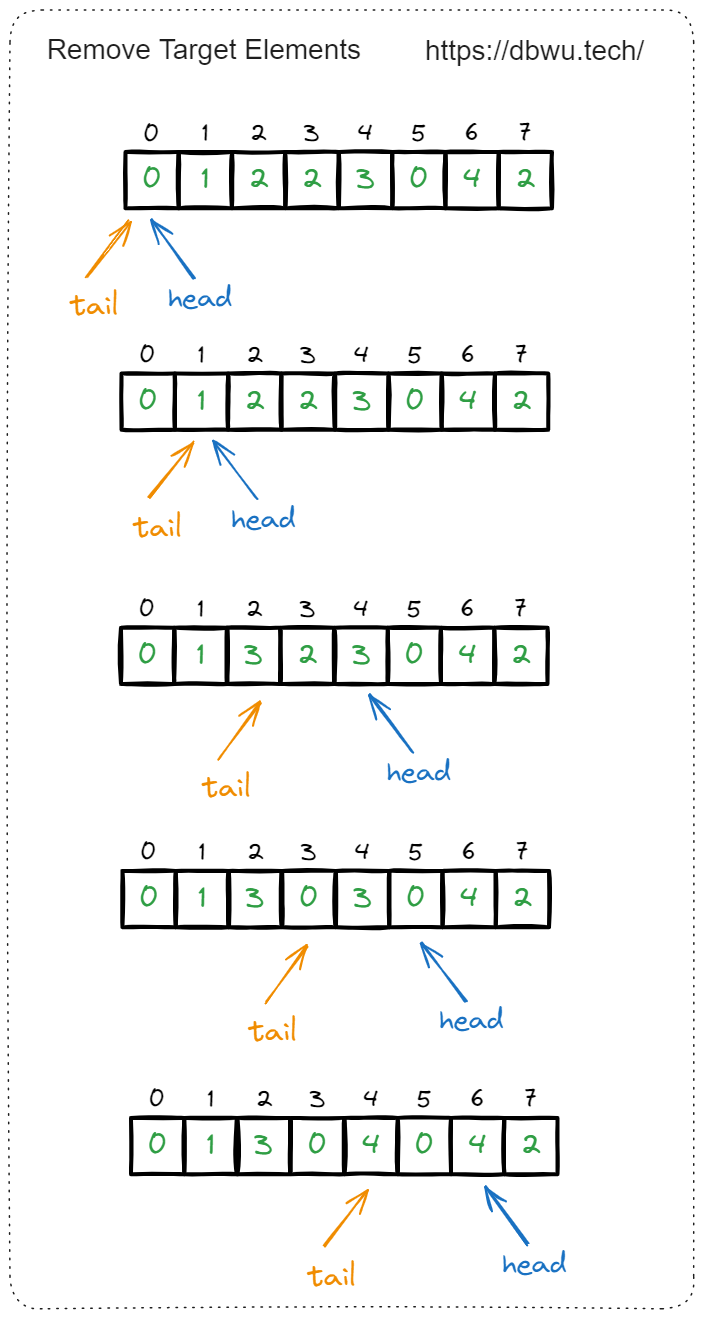
2. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
# 示例来自: https://leetcode.cn/
# 示例 - 1
输入:nums = [3, 2, 2, 3], val = 3
输出:2, nums = [2, 2]
# 示例 - 2
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,3,0,4]
快速套模板:
- 定义头指针为 head, 尾指针为 tail
- head 作为遍历数组索引
- tail 作为更新 数组中值不等于 val的索引
- 最终返回 tail 指针
// 题解代码
func removeElement(nums []int, val int) int {
tail := 0
for head := range nums {
if nums[head] != val {
nums[tail] = nums[head]
tail++
}
}
return tail
}
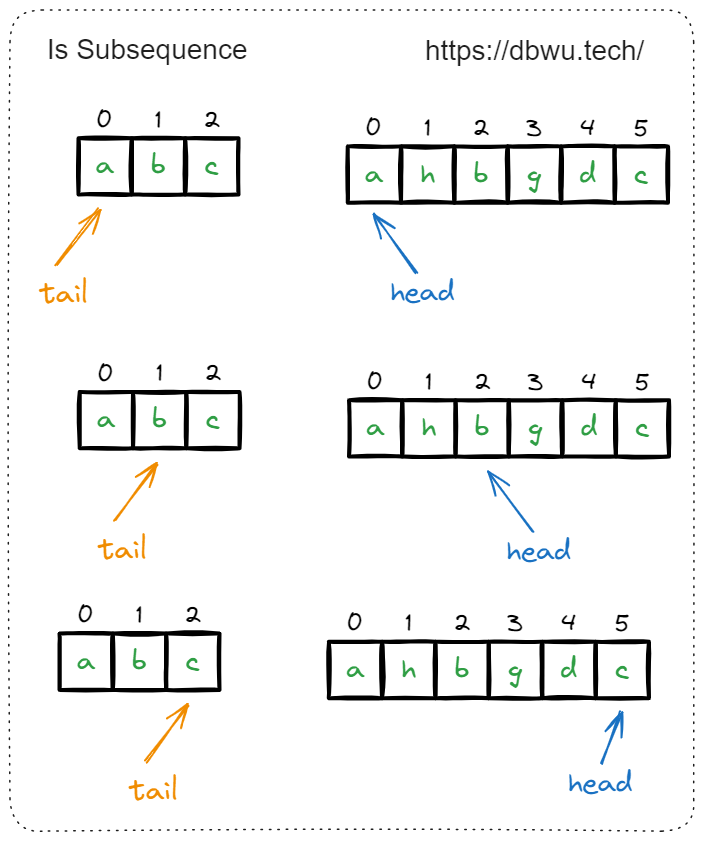
3. 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
# 示例来自: https://leetcode.cn/
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false
快速套模板:
- 定义头指针为 head, 尾指针为 tail
- head 作为遍历字符串 t 的索引
- tail 作为更新 子字符串 s 中当前需要检测字符的索引
- 最终返回 tail 指针
// 题解代码
func isSubsequence(s string, t string) bool {
// 如果子字符串为空,就必然属于子集合
// (Tips: 空字符串也属于子集合之一)
sLen, tLen := len(s), len(t)
tail, head := 0, 0
for tail < sLen && head < tLen {
if s[tail] == t[head] {
tail++
}
head++
}
return tail == sLen
}
4. 找出字符串中第一个匹配项的下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
# 示例来自: https://leetcode.cn/
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
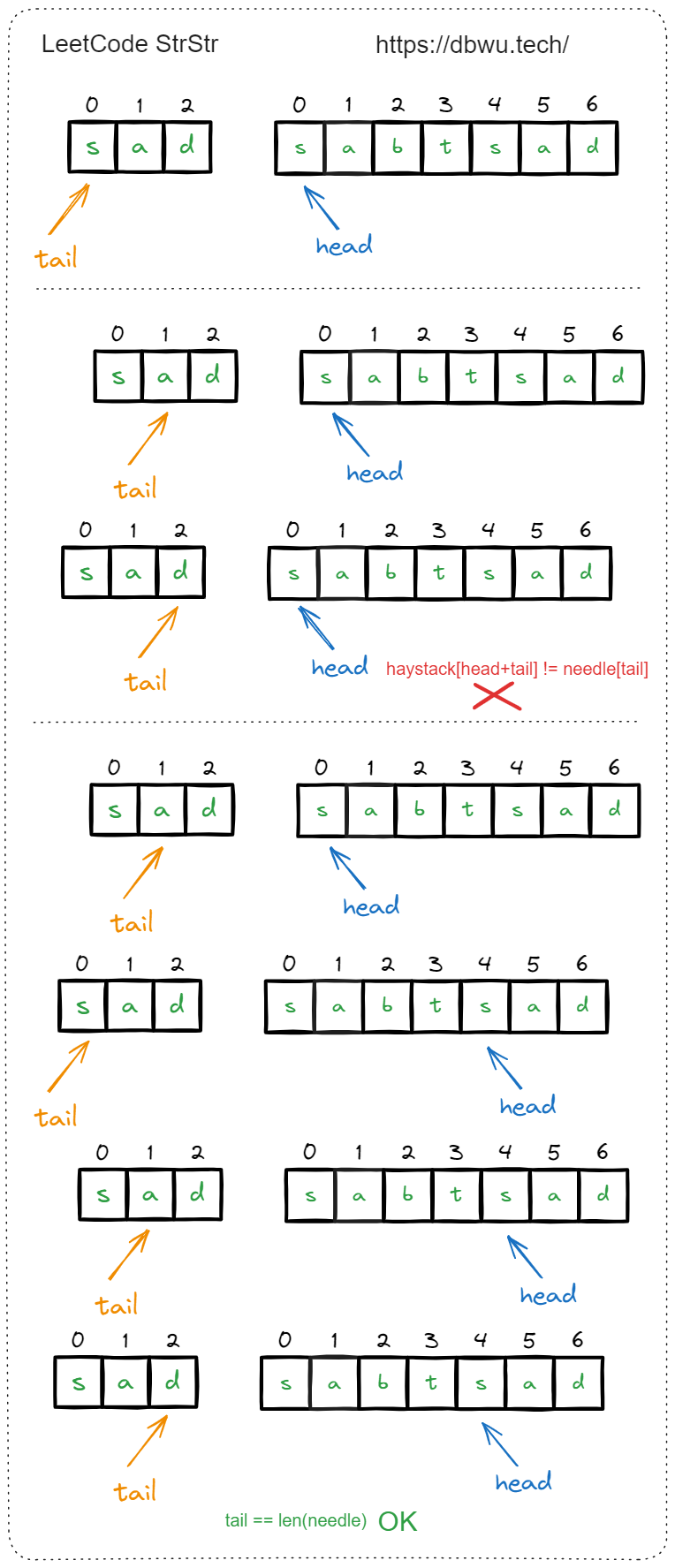
快速套模板:
- 定义头指针为 head, 尾指针为 tail
- head 作为遍历字符串 haystack 的索引
- tail 作为更新 子字符串 needle 中当前需要检测字符的索引
- 最终返回 tail 指针
需要注意的是: 不需要遍历到整个 haystack 字符串,只需要遍历匹配 haystack 字符串减去子字符串 needle 的长度即可,因为再往后面扫描也不可能匹配到了,而且还会引发下标访问越界问题。
// 题解代码
func strStr(haystack string, needle string) int {
n, m := len(haystack), len(needle)
// 例如 haystack = "helloworld", needle = "abc"
// 那么 head 指针最终只需要到 r 即可
// 只需要遍历到 len(haystack) - len(needle)
for head := 0; head <= n-m; head++ {
tail := 0
for ; tail < m; tail++ {
// 任意字符不匹配,直接从 haystack 的下个字符再次进行匹配
if haystack[head+tail] != needle[tail] {
break
}
}
if tail == m {
return head
}
}
return -1
}
💡 左右双指针
左右双指针的典型使用场景是:
- 左指针 从数组/字符串的起始位置开始向后遍历,直到和右指针相遇
- 右指针 从数组/字符串的结束位置开始向前遍历,直到和左指针相遇
1. 验证回文串
给你一个字符串 s,如果它是 回文串。
# 示例来自: https://leetcode.cn/
示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
示例 2:
输入:s = "race a car"
输出:false
解释:"raceacar" 不是回文串。
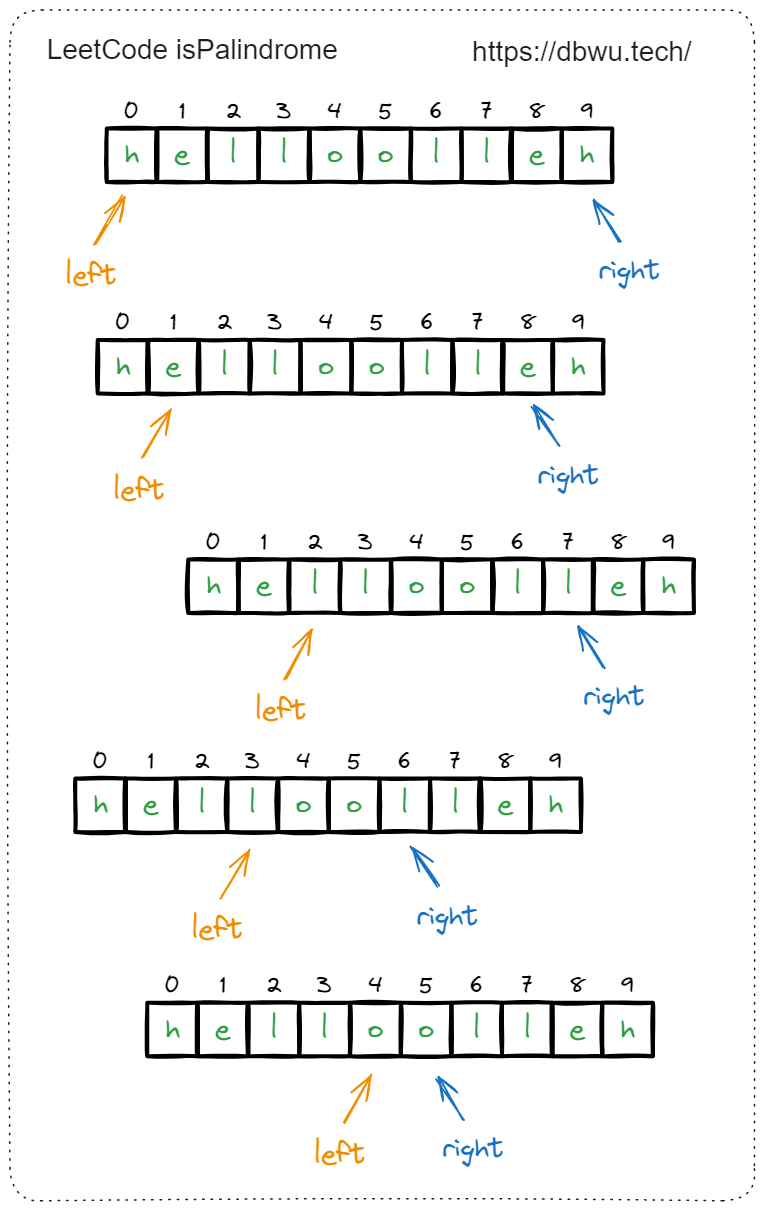
快速套模板:
- 定义左指针为 left, 右指针为 right
- left 指针从左向右开始遍历,每次移动 1 个位置 (不包括无效字符的位置)
- right 指针从右向左开始遍历,每次移动 1 个位置 (不包括无效字符的位置)
- 如果遍历过程中,left 和 right 指向的字符不相等,直接返回 false
- 如果 left 和 right 两个指针相遇或者循环结束,说明字符串为回文字符串
// 题解代码
func isPalindrome(s string) bool {
s = strings.ToLower(s)
left, right := 0, len(s)-1
// 左右指针未相遇时
// 比较当前左右指针指向的字符是否相等
for left < right {
// left 指针从左向右开始遍历
for left < right && !isChar(s[left]) {
left++
}
// right 指针从右向左开始遍历
for left < right && !isChar(s[right]) {
right--
}
// 如果遍历过程中,left 和 right 指向的字符不相等,直接返回 false
if s[left] != s[right] {
return false
}
// left 每次移动 1 个位置
left++
// right 每次移动 1 个位置
right--
}
return true
}
// 辅助方法,判断字符是否为有效的比较字符
func isChar(c byte) bool {
return (c >= 'a' && c <= 'z') || (c >= '0' && c <= '9')
}
2. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
解题思路:
虽然数组有序,但是数组中包含了负数,负数平方可能大于正数平方,例如数组 [-10, 1, 2, 5] 中最小的负数平方之后大于最大的正数,而且题目要求使用复杂度为 O(N) 的算法来解决,这也就意味着不能对数组进行排序。也就是说,在计算出元素平方值的同时就要将其插入到新的排序数组中。
数组中包含了负数和整数,我们可以定义两个指针,分别指向数组的起始位置和结束位置 (也就是最小的负数和最大的整数),然后比较两者的平方值,并将其中较大者(也就是数组所有元素平方后的最大值)放入数组,需要注意的是:放入平方值元素的时候,应该放入新数组末尾位置,然后更新对应的左右指针位置,以此类推,放入第二个、第三个 … 第 N 个排序平方值元素。
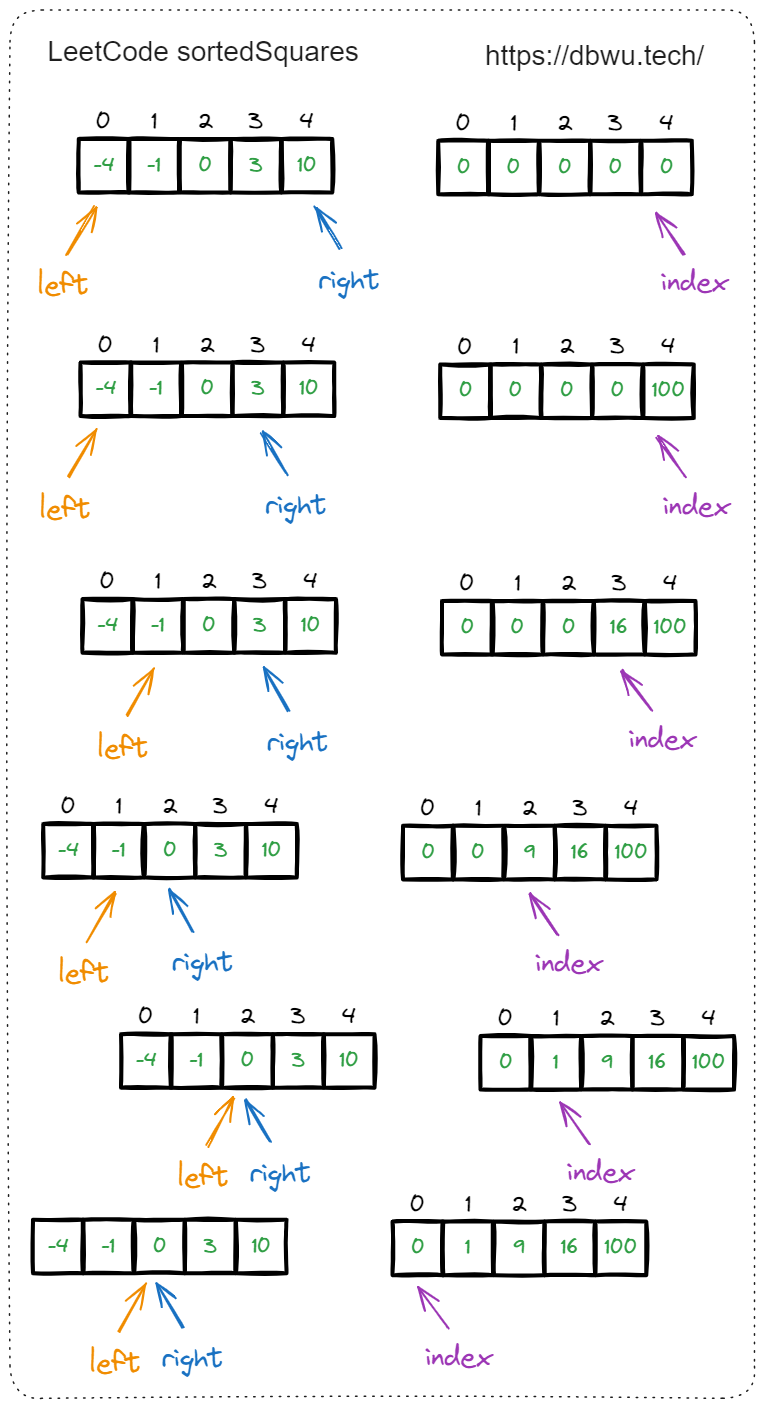
快速套模板:
- 定义左指针为 left, 右指针为 right, 返回值数组 res
- 此外定义一个索引指针 index, 用于更新返回值数组 res 的当前插入位置
- left 指针从左向右开始遍历
- right 指针从右向左开始遍历
- 比较当前 left 和 right 指向的两个值的平方值,并将较大的平方值插入到 res 返回值数组
- 如果 left 指向的平方值大,left 向后移动 1 个位置
- 如果 right 指向的平方值大,right 向前移动 1 个位置
- 每次插入元素后,更新 index 索引指针
// 题解代码
func sortedSquares(nums []int) []int {
// 数组有序,但是负数平方可能大于正数平方
// 例如 [-10, 1, 2, 5] 最小的负数平方之后大于最大的正数
// 所以新数组从后往前插入元素
// 左右双指针,根据平方后数值大小选择前进 OR 后退
// 每次比较左右两个数,即使出现负数也 OK, 因为负数越小,其平方值越大
n := len(nums)
res := make([]int, n)
left, right := 0, n-1
for index := right; index >= 0; index-- {
// 比较当前 left 和 right 指向的两个值的平方值
// 并将较大的平方值插入到 res 返回值数组
if x, y := nums[left]*nums[left], nums[right]*nums[right]; x > y {
res[index] = x
// 如果 left 指向的平方值大,left 向后移动 1 个位置
left++
} else {
res[index] = y
// 如果 right 指向的平方值大,right 向前移动 1 个位置
right--
}
}
return res
}
3. 两数之和 II
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。
# 示例来自: https://leetcode.cn/
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
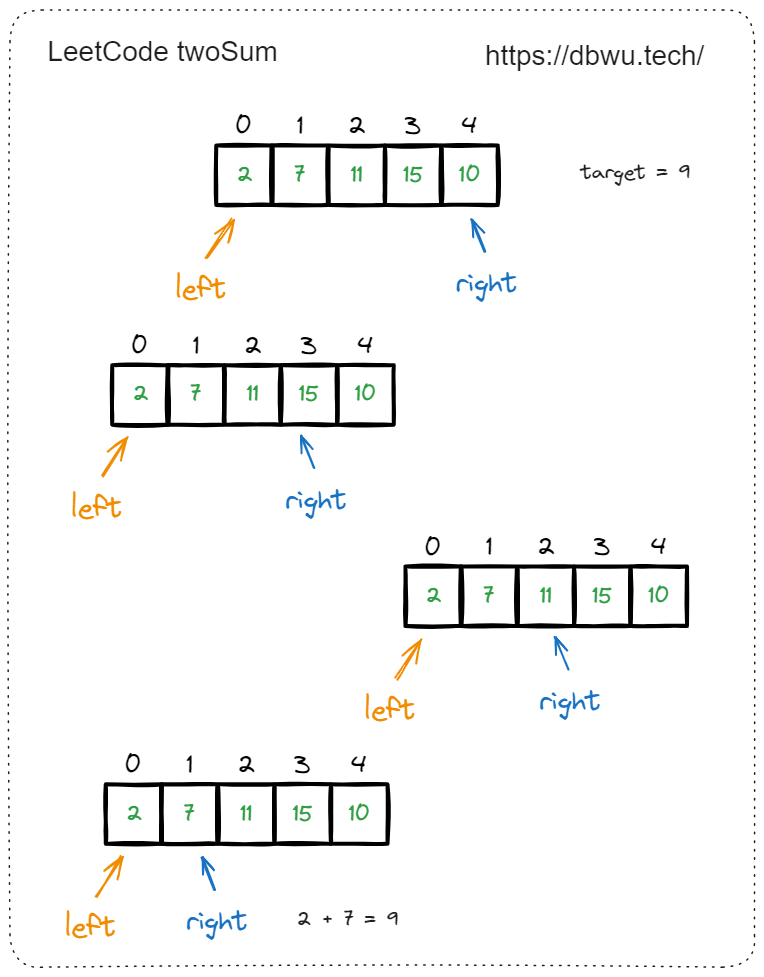
快速套模板:
- 定义左指针为 left, 右指针为 right
- left 指针从左向右开始遍历,每次移动 1 个位置
- right 指针从右向左开始遍历,每次移动 1 个位置
- 遍历过程中,比较当前 left 和 right 指向的两个元素之和 sum 和目标值 target,如果相等,直接返回 left 和 right 两个指针索引值 (题目要求数组下标从 1 开始,所以指针返回前 + 1)
- 如果 sum 大于 target, 说明需要减小当前 sum, 此时将右指针向前移动 1 位 (因为数组是有序的,移动之后再次 left 和 right 再次相加,sum 会减小)
- 如果 sum 小于 target, 说明需要增大当前 sum, 此时将左指针向后移动 1 位 (因为数组是有序的,移动之后再次 left 和 right 再次相加,sum 会增大)
func twoSum(numbers []int, target int) []int {
res := []int{}
for left, right := 0, len(numbers)-1; left < right; {
sum := numbers[left] + numbers[right]
if sum == target {
// 题目声明下标从 1 开始,所以这里将两个索引各加 1
return []int{left + 1, right + 1}
}
if sum > target {
right--
} else {
left++
}
}
return res
}
4. 盛最多水的容器
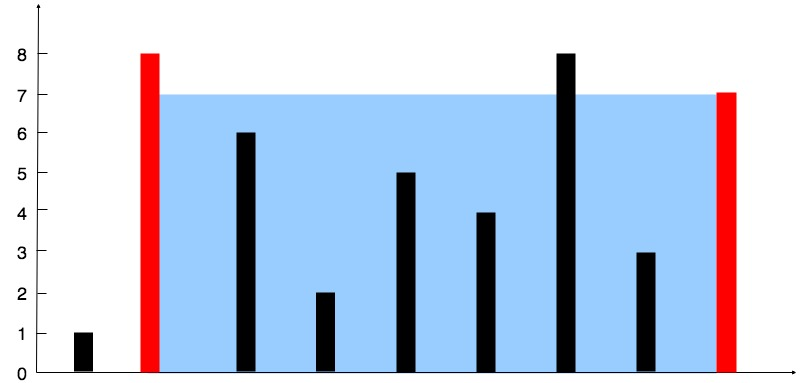
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
# 示例来自: https://leetcode.cn/
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
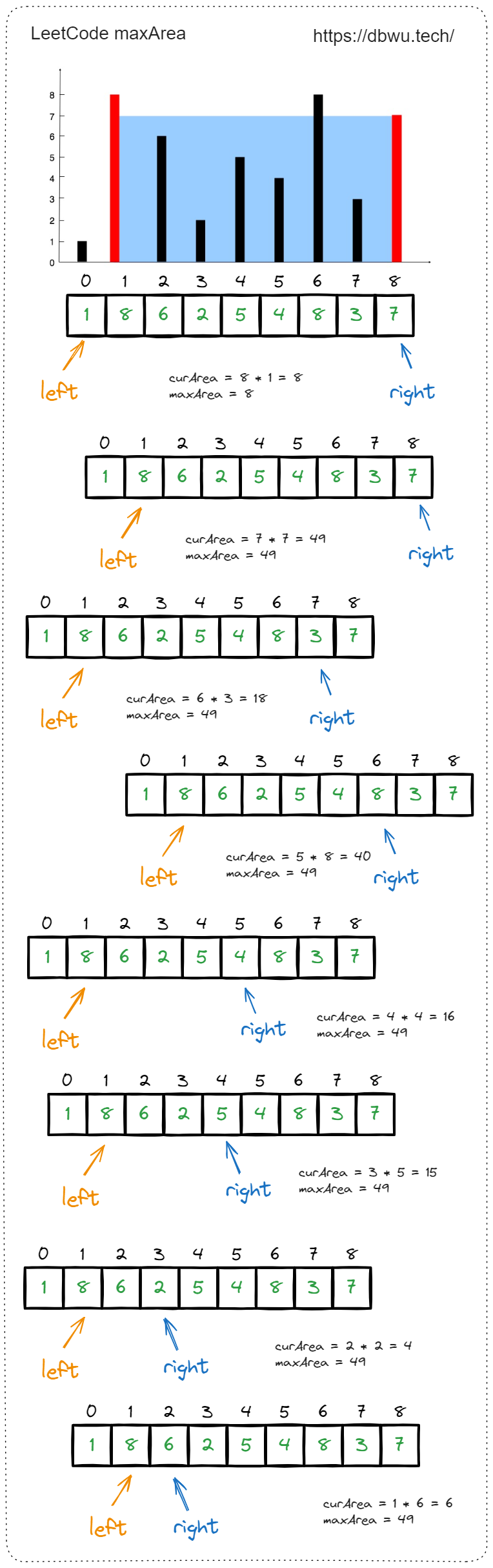
解题思路:
题目要求计算出一个最大平面区域,这个区域可以看作一个矩形,矩形的长度是 X 轴左右两个指针的间距,宽度是 Y 轴左右两 个指针中的较小值。
快速套模板:
- 定义左指针为 left, 右指针为 right
- left 指针从左向右开始遍历,每次移动 1 个位置
- right 指针从右向左开始遍历,每次移动 1 个位置
- 以 left 和 right 的间距作为当前矩形的长度
- 以 left 和 right 中的较小值作为当前矩形的宽度
- 如果 left 小于 right, 说明向后移动左指针,可能会得到更大的矩形面积,移动 left 指针
- 如果 left 大于等于 right, 说明向前移动右指针,可能会得到更大的矩形面积,移动 right 指针
// 题解代码
func maxArea(height []int) int {
left, right := 0, len(height)-1
res := 0
for left < right {
// 表示当前矩形的长度
width := right - left
// 表示当前矩形的宽度 (低水位)
low := 0
if height[left] < height[right] {
low = height[left]
left++
} else {
low = height[right]
right--
}
// 更新已知的最大矩形
res = max(res, width*low)
}
return res
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
💡 无序双指针
如果需要使用双指针解题,但是两个指针没有任何语义和逻辑顺序,只是用于指向不同的地址,那么可以使用无序指针。
1. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 递增顺序 排列。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
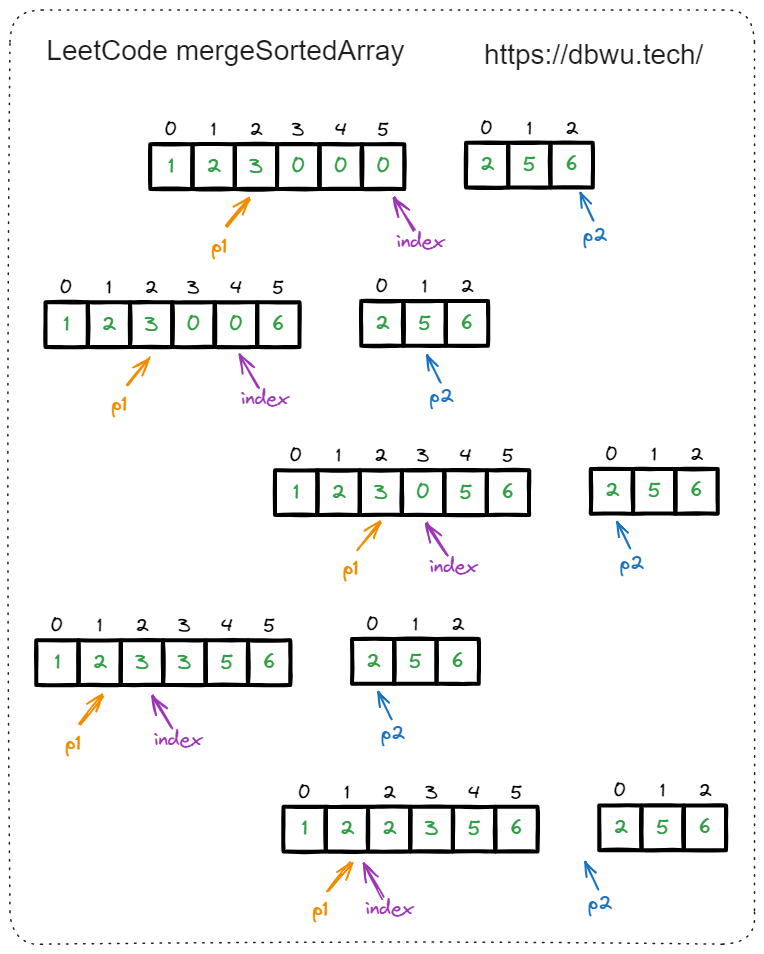
解题思路:
通过观察题目给的参数和用例可以看到,nums1 数组的后半部分是空的 (全部由 0 填充),因为 nums1 数组的容量要足够容纳 nums1 和 nums2 的所有元素,所以反过来看,可以从后向前扫描,每次取两个数组中较大的数字放在 nums1 数组的末尾,然后索引递减。
快速套模板:
- 定义两个无序指针 p1, p2
- 此外还需要定义一个索引指针 index,表示后向前更新数组元素时的当前索引
- p1 指针从右向左开始遍历数组 nums1
- p2 指针从右向左开始遍历数组 nums2
- 单次遍历过程中,取出 p1 和 p2 中的较大值,放入索引指针 index 当前指向的位置
- 如果 p1 指针指向的值更大,p1 指针向左移动 1 个位置,反之 p2 指针向左移动 1 个位置
- 将索引指针向左移动 1 个位置
- 循环结束后,处理一下数组 nums2 可能存在的边界情况
// 题解代码
func merge(nums1 []int, m int, nums2 []int, n int) {
// 三个指针都是从右向左移动
index := m+n-1
p1, p2 := m-1, n-1
for p1 >= 0 && p2 >= 0 {
if nums1[p1] > nums2[p2] {
// p1 指向的值更大
nums1[index] = nums1[p1]
p1--
} else {
// p2 指向的值更大
nums1[index] = nums2[p2]
p2--
}
index--
}
// 题目假设 nums1 的空间大小等于 m + n
// 这样它就有足够的空间保存来自 nums2 的元素
// 所以这里 p2 存在两种情况
// (1) == 0 说明两个数组中最小的元素在 nums1,无需调整
// (2) > 0 说明两个数组中最小的元素在 nums2,仅调整 nums2 中剩余元素
for p2 >= 0 {
nums1[index] = nums2[p2]
index--
p2--
}
}
2. 汇总区间
给定一个 无重复元素 的 有序 整数数组 nums 。返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [0,1,2,4,5,7]
输出:["0->2","4->5","7"]
解释:区间范围是:
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"
示例 2:
输入:nums = [0,2,3,4,6,8,9]
输出:["0","2->4","6","8->9"]
解释:区间范围是:
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"
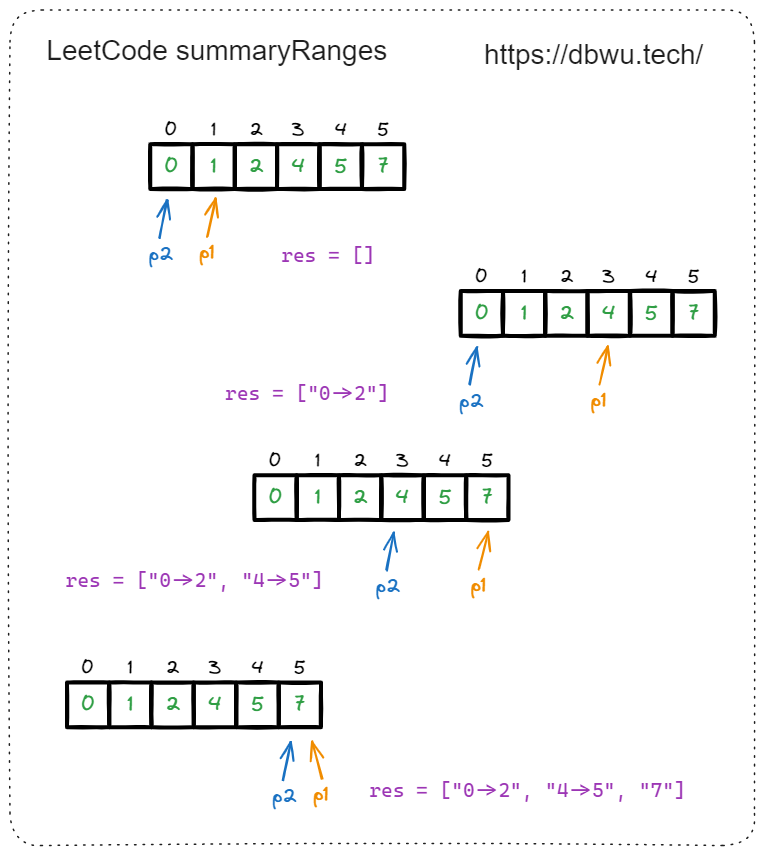
快速套模板:
- 定义两个无序指针 p1, p2
- p1 指针从左向右开始遍历
- p2 指针从左向右开始遍历
- 单次遍历过程中,将 p2 指向 p1 当前位置,p1 继续内部循环向前扫描,直到遇到非连续元素结束循环
- 将 p2 和 p1 指向的元素加入到结果集中
// 题解代码
func summaryRanges(nums []int) []string {
var res []string
for p1, n := 0, len(nums); p1 < n; {
// p2 指向 p1 的当前位置
p2 := p1
p1++
// 只要元素是连续的,p1 指针继续向前扫描
for p1 < n && nums[p1] == nums[p1-1]+1 {
p1++
}
s := strconv.Itoa(nums[p2])
// 如果 p2 和 p1 不是连续元素
// 说明区间发生了合并
if p2 < p1-1 {
s += "->" + strconv.Itoa(nums[p1-1])
}
res = append(res, s)
}
return res
}
💡 三指针
双指针除了前文中提到几种常用的类型外,还有一种衍生类型: 多指针,比如下面的这个三指针问题。
1. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
# 示例来自: https://leetcode.cn/
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
解题思路:
虽然题目要求的是计算出所有三元组,但是我们可以将其 “降维” 到双指针问题:
对于数组中的每个元素 X,找出另外两个元素,要求这两个元素的和为 0 - X。
这就是前文中提到过的原题了: 两数之和 II,可以使用左右双指针来快速解题,但是因为题目给出的数组是无序的,所以为了满足左右双指针的应用条件,需要先对数组进行排序。
快速套模板:
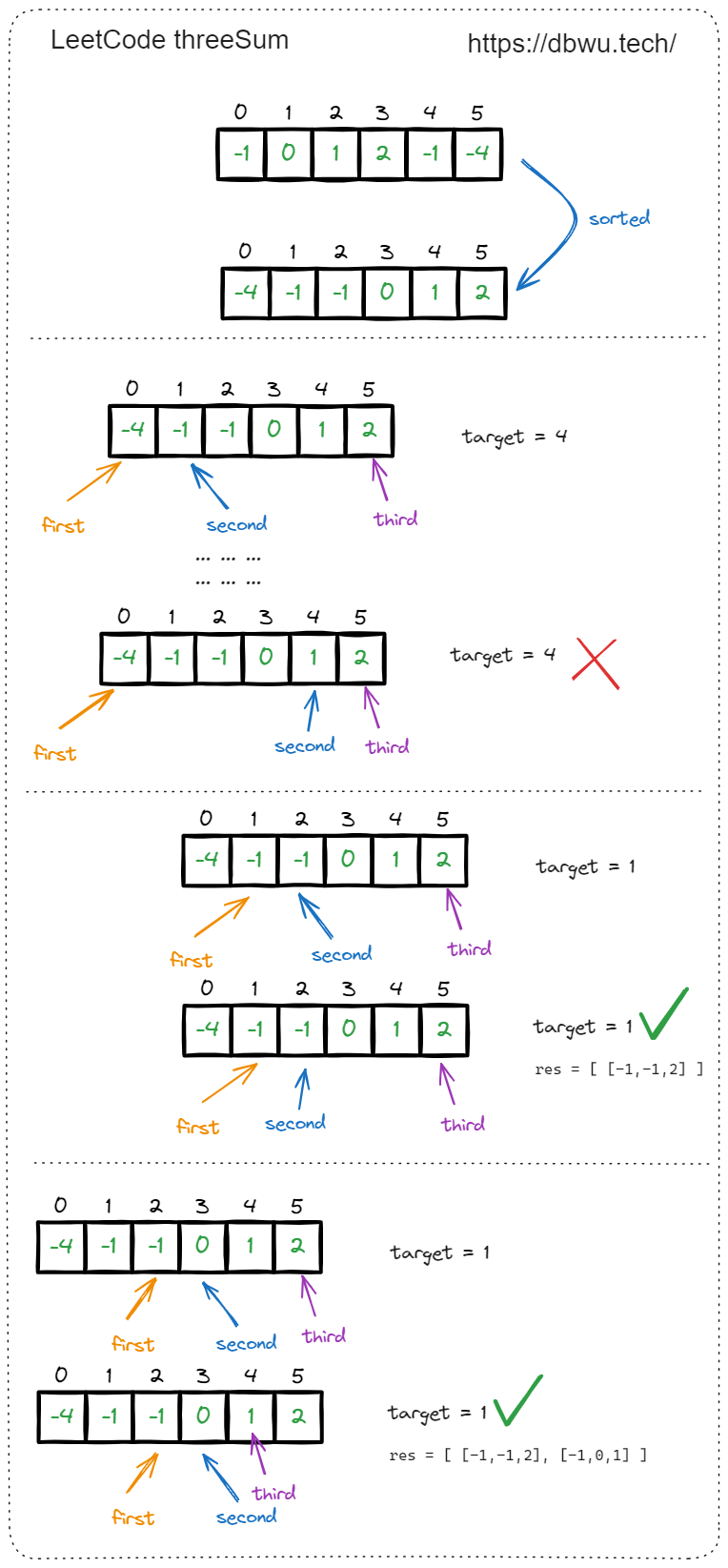
- 定义三个指针 first second third
- first 指针从左向右开始遍历,作为最外层循环
- second 和 third 充当左右双指针,作为内层循环查找和为
0 - nums[first]的两个值 ,其中:- second 指针指向 first + 1 的位置,从左向右开始遍历
- third 指针指向数组的末尾位置,从右向左开始遍历
- 如果当前 second 和 third 指向的两个值的和为
0 - nums[first], 将三个指针指向的当前元素加入到结果集中
// 题解代码
func threeSum(nums []int) [][]int {
n := len(nums)
// 先对数组进行排序
sort.Ints(nums)
res := make([][]int, 0)
for first := 0; first < n; first++ {
// 需要和上一次枚举的数不相同
if first > 0 && nums[first] == nums[first-1] {
continue
}
// 内部循环就是一个典型的左右双指针代码
// 对应的指针初始指向数组的最右端
third := n - 1
// 查找的目标值是 0 - 当前外层元素 (nums[first])
// 也就是 -1 * nums[first]
target := -1 * nums[first]
for second := first + 1; second < n; second++ {
// 需要和上一次枚举的数不相同
if second > first+1 && nums[second] == nums[second-1] {
continue
}
// 需要保证 second 的指针在 third 的指针的左侧
for second < third && nums[second]+nums[third] > target {
third--
}
// 如果指针重合,随着 second 后续的增加
// 就不会有满足 first+second+third=0 && second<third 的 third 了,可以退出循环
if second == third {
break
}
if nums[second]+nums[third] == target {
res = append(res, []int{nums[first], nums[second], nums[third]})
}
}
}
return res
}