布谷鸟过滤器
基本概念
布谷鸟过滤器 是一种节省内存空间的概率数据结构,基于 布谷鸟哈希算法 实现的过滤器,和 布隆过滤器 一样,用于检测指定元素是否存在于某个集合中,返回 元素一定不存在 或 有较大可能存在。
和布隆过滤器比较
优点
- 布谷鸟过滤器支持删除元素,布隆过滤器不支持
- 高负载因子场景下,布谷鸟过滤器查询效率更高
- 对于存储数据量较大且期望误判率较低 (< 3%) 的场景下,布谷鸟过滤器存储空间开销更低
- 布谷鸟过滤器比布隆过滤器更容易实现
缺点
- 布谷鸟过滤器采用一种备用候选桶的方案,候选桶与首选桶可以通过
位置 VS 值指纹的哈希通过异或计算得出,这种对应关系要求桶的大小必须是 2 的指数倍 - 布隆过滤器插入时计算好哈希直接写入位即可,而布谷鸟过滤器在计算后可能会出现对应位置上已经存储了指纹,这时就需要将已存储的值踢出到候选桶,碰撞概率和插入耗时随着表元素增多而增大,因此其插入性能低于布隆过滤器
- 布隆过滤器插入重复元素时没有影响 (可以重复插入),而布谷鸟过滤器对已存在的值会做
踢出操作,因此重复元素的插入存在上限 - 布谷鸟过滤器的删除并不完美,删除操作在相同哈希值仅被插入一次时是完美的,如果元素没有插入就进行删除,可能会出现误删除 (删除了相同哈希值的其他元素), 如果元素插入了多次,那么每次删除操作只删除一个值,那么就需要知道元素插入了多少次才能彻底删除,或者循环删除直到失败为止
PS: 如果只需要保证 一定不存在 语义,那么删除时,不论是否存在重复元素,只删除一次即可。
布谷鸟哈希算法描述
- 使用两个哈希函数
H1,H2和两个哈希表T1,T2 - 插入元素 x
- 计算 x 的两个哈希值
idx1 = H1(x),idx2 = H2(x) - 如果
T1[idx1],T2[idx2]有一个为空,插入 x, 两者都为空,随便选一个插入 x - 如果
T1[idx1],T2[idx2]都不为空,则随便选择其中一个 (设为y) 将其踢出,插入x - 重复上述过程,插入元素
y - 如果插入时,踢出次数过多,则说明哈希表满了,进行扩容 (
ReHash),扩容完成后再次插入
- 计算 x 的两个哈希值
- 查询元素 x
- 读取
T1[idx1],T2[idx2]的值,和 x 比较
- 读取
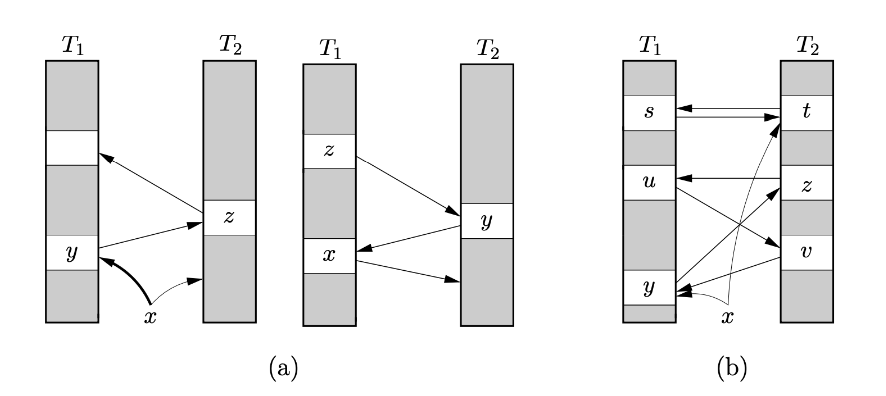
图(a) 算法过程描述:
- 插入元素 x
- 将对应桶的元素 y 踢出
- 将元素 y 插入到桶 z
- 将对应桶的元素 z 踢出
- 将元素 z 插入到其他桶中
图(b) 算法过程描述:
- 插入元素 x
- 插入失败,因为桶已经满了
- 触发扩容
伪代码
按照算法描述,翻译成伪代码如下 (不考虑并发情况):
package main
import (
"math/rand"
"time"
)
const (
TSize = 1024 // 假设表的大小为 1024
)
var (
T1 = make(map[int]any, TSize) // 哈希表 1
T2 = make(map[int]any, TSize) // 哈希表 2
)
// 哈希函数 1
// 返回随机数作为哈希值
func H1(x any) int {
rand.Seed(time.Now().UnixNano())
return rand.Intn(TSize)
}
// 哈希函数 2
// 返回随机数作为哈希值
func H2(x any) int {
rand.Seed(time.Now().UnixNano())
return rand.Intn(TSize)
}
// 扩容操作,这里省略具体实现
func ReHash() {
// do something
}
// 随机踢出一个元素
// 返回踢出的哈希桶编号以及元素索引
func KicksOut(x any) any {
// 哈希桶已满
if len(T1) == TSize && len(T2) == TSize {
return nil
}
rand.Seed(time.Now().UnixNano())
n := rand.Intn(2)
var y any // 被踢出的元素 y
// 直接利用 Go map 的无序遍历特性
// 遍历时将 [第一个元素] 作为随机元素踢出
if n == 0 {
// 从 T1 桶随机选择一个元素踢出
for k, v := range T1 {
// 将 x 插入到 y 的桶 (覆盖式)
T1[k] = x
y = v
break
}
} else {
// 从 T2 桶随机选择一个元素踢出
for k, v := range T2 {
// 将 x 插入到 y 的桶 (覆盖式)
T2[k] = x
y = v
break
}
}
return y
}
// 插入元素
func Insert(x any) bool {
idx1, idx2 := H1(x), H2(x)
// 如果 T1 桶对应桶为空,则插入 T1
if _, ok := T1[idx1]; !ok {
T1[idx1] = x
return true
}
// 如果 T2 桶对应桶为空,则插入 T2
if _, ok := T2[idx2]; !ok {
T2[idx2] = x
return true
}
y := KicksOut(x)
// 哈希桶已满,进行扩容
if y == nil {
ReHash()
}
// 插入元素 y
return Insert(y)
}
不同的版本
一个哈希桶
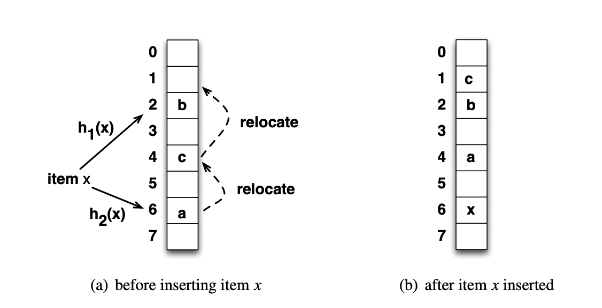
如图所示,在未发生哈希碰撞之前,哈希桶的利用率只有 50%。
四路哈希桶
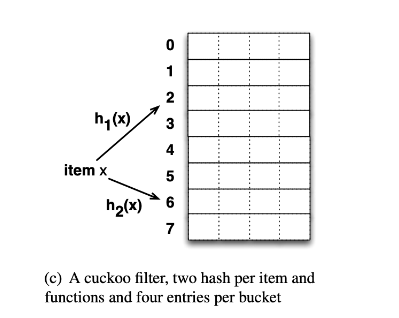
如图所示是一个改进的哈希桶,每个桶有 4 个槽位,当哈希函数映射到同一个桶时,其它 3 个槽位如果有空位,那么就不会有元素被踢出,降低了碰撞概率。
布谷鸟过滤器
布谷鸟过滤器 对 布谷鸟哈希算法 进行了如下优化改进:
- 使用多路哈希桶提高桶的利用率
- 只存储 key 的指纹以减少内存使用
通过异或计算寻找新桶
异或计算性质: 三个值任意两个值进行异或计算,都可以得出第三个值。
示例代码: 数字 1, 2, 3 执行异或计算
package main
func main() {
println(1 ^ 2) // 3
println(3 ^ 1) // 2
println(3 ^ 2) // 1
}
布谷鸟过滤器 为了节省内存,保存的是 x 的指纹信息,而非源值,那么当某个元素 x 被踢出时,需要找一个新桶 h2(x),如何在不损失 x 的指纹信息的情况下,计算新桶 (候选桶) 并存储呢?
布谷鸟过滤器 采用了巧妙的算法: 将桶 h1(x) 和对应的指纹哈希值 hash( finger(x) ) 进行 异或计算 得出新的桶,这样当新桶的值后面被踢出时,
可以通过 异或计算 得到 x 的指纹信息。
对于元素 x, 计算两个哈希值:
h1(x) = hash(x), h2(x) = h1(x) ⊕ hash(x’s fingerprint)
踢出桶上的元素时 (不管该桶是 h1(x) 还是 h2(x)),直接使用当前桶的索引 index 和存储在桶中的指纹信息计算备用桶 j
j = i ⊕ hash(fingerprint)
均衡分配
此外,指纹与桶进行 异或计算 之前会进行哈希,从而在表中均衡分配。如果备用位使用 i ⊕ hash(fingerprint) 计算时不将指纹进行哈希,且指纹的大小与表的大小相比很小,那么踢出的元素最终会落在邻近的桶。
例如使用 8 位指纹,踢出的元素将被放置到离桶 i 最多 256 (2^8) 的桶,因为 异或计算 将改变桶索引的低 8 位,而高位不会改变。
哈希指纹可以确保这些元素可以重新定位到哈希表的不同的桶中,达到均衡分配,减少哈希碰撞并提高表的利用率。
空间优化
较大的桶可以提高表的利用率,使用 2 个哈希函数,桶大小为 1 时,负载因子为 50% (上面提到的第一种布谷鸟哈希算法版本),
但是当使用桶大小 2, 4, 8 时,负载因子分别会增加到 84%, 95%, 98%。
实验数据表明,当误判率 r > 0.002 时,每个桶使用 2 个槽位比 4 个槽位效果更好,当 r 为到 0.00001 < r ≤ 0.002 时,每个桶 4 个槽位可以最小化空间。
半排序桶
半排序的本质是: 对每个指纹取 4 位,该 4 位可以表示为一个 16 进制,对于 b 个指纹的 4 位存储就可以表示为 b 个 16 进制,进行 重复组合计算 后, 可以通过索引其位置来找到对应的指纹 (也就是某个组合值)。
假设每个桶包含 b = 4 个指纹,每个指纹 f = 4 bit,一个未压缩的桶占 4 x 4 = 16 bit。但是如果我们对每个 4 位指纹进行排序(空项被视为存储值为 “0” 的指纹),
那么共有 3876 个重复组合值。如果我们预先计算并将 3876 个值存储在一个额外的表中 (表中每个位置表示一个指纹组合),并将桶替换为预先计算好的表,
那么桶可以用 12 bit 表示整个表 (2 ^ 12 = 4096 > 3876),而不是 16 bit 表示桶,这样算下来,每个指纹可以节省 1 bit。
3876 是怎样计算出来的?
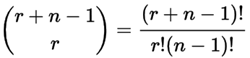
其中 n 表示被选择的东西个数, r 表示选择个数,(顺可以重复)。
根据数学公式,我们可以编写如下代码:
package main
import "fmt"
// 计算重复组合数量
func multiCombination(n, r int) int {
if n == 0 || r == 0 {
return 0
}
numerator := 1
denominator := 1
for i := 1; i <= r; i++ {
numerator *= n + i - 1
denominator *= i
}
return numerator / denominator
}
func main() {
fmt.Printf("n = %d, r = %d, combinations = %d\n", 16, 4, multiCombination(16, 4))
}
在上面的代码中,计算了在 16 bit 中 4 bit 指纹的重复组合数量。
$ go run main.go
# 输出如下
n = 16, r = 4, combinations = 3876
开源库
笔者选择由开源的 linvon/cuckoo-filter 作为研究 布谷鸟过滤器 代码实现,版本为 v0.4.0。
这个库的优点
这里直接引用库作者的原文:
在翻阅了 Github 上 cuckoofilter 的 golang 实现后,发现已有的实现都存在一些缺点:
- 绝大部分的库都是固定 b 和 f 的,即假阳性率也是固定的,适应性不好
- 所有的库 f 都是以字节为单位的,只能以 8 的倍数来调整,不方便调整假阳性率
- 所有的库都没有实现半排序桶,相比于布隆过滤器的优势大打折扣
因为作者的场景需要更优的空间和自定的假阳性率,因此移植了原论文的 C++ 实现,并做了一些优化,主要包括:
- 支持调节参数
- 支持半排序桶
- 压缩空间到紧凑的位数组,按位存储指纹
- 支持二进制序列化
示例
package main
import (
"fmt"
"github.com/linvon/cuckoo-filter"
)
func main() {
// 初始化一个布谷鸟过滤器
// 使用半排序桶
// 每个桶包含 4 个指纹, 每个指纹 4 bits
// 最大存放元素数量 4096
cf := cuckoo.NewFilter(4, 4, 1<<12, cuckoo.TableTypePacked)
// 添加一些元素
cf.Add([]byte(`Hello World`))
cf.Add([]byte(`Hello Golang`))
// 检测元素是否存在
fmt.Printf("%v\n", cf.Contain([]byte(`Hello World`)))
fmt.Printf("%v\n", cf.Contain([]byte(`Hello Golang`)))
fmt.Printf("%v\n", cf.Contain([]byte(`Hello Rust`)))
// 输出元素数量
fmt.Printf("filter size = %d\n", cf.Size())
// 删除元素
cf.Delete([]byte(`Hello World`))
// 输出过滤器信息
fmt.Println("\n", cf.Info())
}
$ go run main.go
# 输出如下
true
true
false
filter size = 2
CuckooFilter Status:
PackedHashtable with tag size: 4 bits
4 packed bits(3 bits after compression) and 0 direct bits
Associativity: 4
Total # of rows: 2048
Total # slots: 8192
Keys stored: 1
Load factor: 0.0001220703125
Hashtable size: 3 KB
bit/key: 24632
源码解析
接口
linvon/cuckoo-filter 实现了 普通单表 和空间优化的 基于半排序桶的压缩表,将两者的通用部分抽象为 table 接口,通过运行时的 工厂方法 可以在初始化时根据不同的参数生成不同的过滤器。
const (
// 普通表
TableTypeSingle = 0
// 压缩表
TableTypePacked = 1
)
type table interface {
...
}
func getTable(tableType uint) interface{} {
switch tableType {
case TableTypePacked:
return NewPackedTable()
default:
return NewSingleTable()
}
}
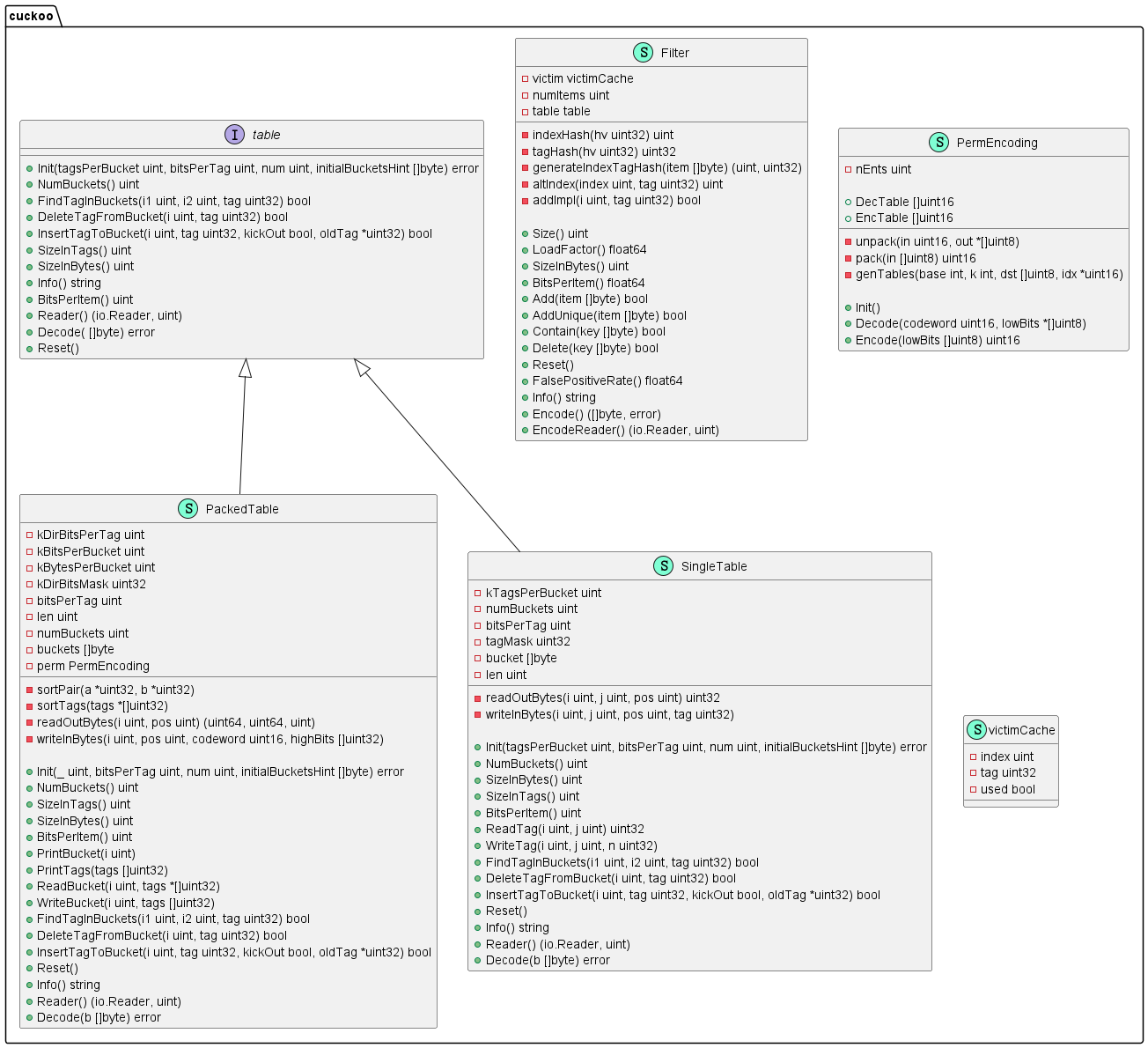
过滤器数据结构
victimCache 结构体表示过滤器执行 Add 操作时被 踢出 的元素对象。
type victimCache struct {
index uint
tag uint32
used bool
}
Filter 结构体表示 过滤器 对象,非常简洁,只有三个字段: 被踢出元素, 元素数量, 底层用于存储的表实例。
type Filter struct {
victim victimCache
numItems uint
table table
}
初始化过滤器
func NewFilter(tagsPerBucket, bitsPerItem, maxNumKeys, tableType uint) *Filter {
// 根据表内存放元素和每个桶的元素指纹数量,计算需要的桶的数量
numBuckets := getNextPow2(uint64(maxNumKeys / tagsPerBucket))
// 如果表的负载因子过高,就将桶的数量扩容 (翻 1 倍)
// 负载因子如何计算出来的呢?
// 框架这里进行了 3 个硬编码的值:
// 默认: 0.99
// 桶大小为 2: 0.85
// 桶大小为 4: 0.96
if float64(maxNumKeys)/float64(numBuckets*tagsPerBucket) > maxLoadFactor(tagsPerBucket) {
numBuckets <<= 1
}
// 桶最少得有 1 个
if numBuckets == 0 {
numBuckets = 1
}
// 工厂方法根据参数类型生成过滤器
table := getTable(tableType).(table)
// 表初始化
_ = table.Init(tagsPerBucket, bitsPerItem, numBuckets, nil)
return &Filter{
table: table,
}
}
添加元素
Add 方法添加一个元素到表中,返回是否添加成功。
func (f *Filter) Add(item []byte) bool {
// 如果被踢出的元素没有找到可用的桶
// 那么继续添加元素只会进入恶行循环,降低性能
// 此时直接返回即可
if f.victim.used {
return false
}
// 计算哈希值和桶索引,然后将元素添加到表中对应的桶
i, tag := f.generateIndexTagHash(item)
return f.addImpl(i, tag)
}
查找元素
Contain 方法检测给定元素是否存在于表中。
func (f *Filter) Contain(key []byte) bool {
// 计算元素的哈希值和桶索引
i1, tag := f.generateIndexTagHash(key)
// 计算候选桶索引
i2 := f.altIndex(i1, tag)
hit := f.victim.used && tag == f.victim.tag && (i1 == f.victim.index || i2 == f.victim.index)
// 满足以下两个条件之一,说明参数元素存在于表中:
// 1. 参数元素和表内被踢出元素的哈希值以及桶位置相同
// 2. 在表的某个桶内找到了相同的参数元素哈希
if hit || f.table.FindTagInBuckets(i1, i2, tag) {
return true
}
return false
}
计算元素数量
Size 方法计算表内当前存储的元素数量,如果 被踢出元素 没有找到可用的桶,元素数量 + 1。
func (f *Filter) Size() uint {
var c uint
if f.victim.used {
c = 1
}
return f.numItems + c
}
计算负载因子
LoadFactor 方法计算当前表的 负载因子, 计算公式为:
表内当前元素数量 / 表内可存储元素数量
func (f *Filter) LoadFactor() float64 {
return 1.0 * float64(f.Size()) / float64(f.table.SizeInTags())
}
重置过滤器
Reset 方法会重置过滤器,相当于重新初始化。
func (f *Filter) Reset() {
// 底层表内元素初始化为 0
f.table.Reset()
// 元素计数归 0
f.numItems = 0
// 重置被踢出元素
f.victim.index = 0
f.victim.tag = 0
f.victim.used = false
}
计算误判率
FalsePositiveRate 方法计算 过滤器 的 误判率,需要注意的是,该方法会调用 Reset 方法重置 过滤器。
func (f *Filter) FalsePositiveRate() float64 {
n1 := make([]byte, 4)
f.Reset() // 重置过滤器
// 获取底层表可存储元素数量
n := f.table.SizeInTags()
// 循环向表内添加元素,元素为 [0 ... n]
for i := uint32(0); i < uint32(n); i++ {
binary.BigEndian.PutUint32(n1, i)
f.Add(n1)
}
// 计算误判率采用的检测次数 (这里硬编码为 10 W)
var rounds uint32 = 100000
// 误判计数
fp := 0
for i := uint32(0); i < rounds; i++ {
// 给定一个不可能存在表中的元素
binary.BigEndian.PutUint32(n1, i+uint32(n)+1)
// 正常情况下,Contain 方法返回的都是 false
if f.Contain(n1) {
// 如果 Contain 方法返回 true, 则属于误判
// 误判计数 + 1
fp++
}
}
f.Reset() // 重置过滤器
// 误判计数 / 检测次数 = 误判率
return float64(fp) / float64(rounds)
}
哈希算法
module github.com/linvon/cuckoo-filter
go 1.14
require github.com/dgryski/go-metro v0.0.0-20200812162917-85c65e2d0165
从 go.mod 文件定义中可以看到,linvon/cuckoo-filter 使用的哈希算法是 MetroHash。
MetroHash是一个哈希函数算法,可用于计算输入数据的64 位和128 位哈希值,支持增量式哈希计算,具有较高的性能和较低的碰撞率概率。
func (f *Filter) altIndex(index uint, tag uint32) uint {
// 0x5bd1e995 是 MurmurHash2 算法的哈希常量
return f.indexHash(uint32(index) ^ (tag * 0x5bd1e995))
}
此外,在计算 候选桶 的索引时,也用到了 Murmur2 算法。
省略部分
普通单表 和 压缩表 的底层表存储实现,由于时间关系不再展开分析,感兴趣的读者可以自行阅读源代码。
调用关系图
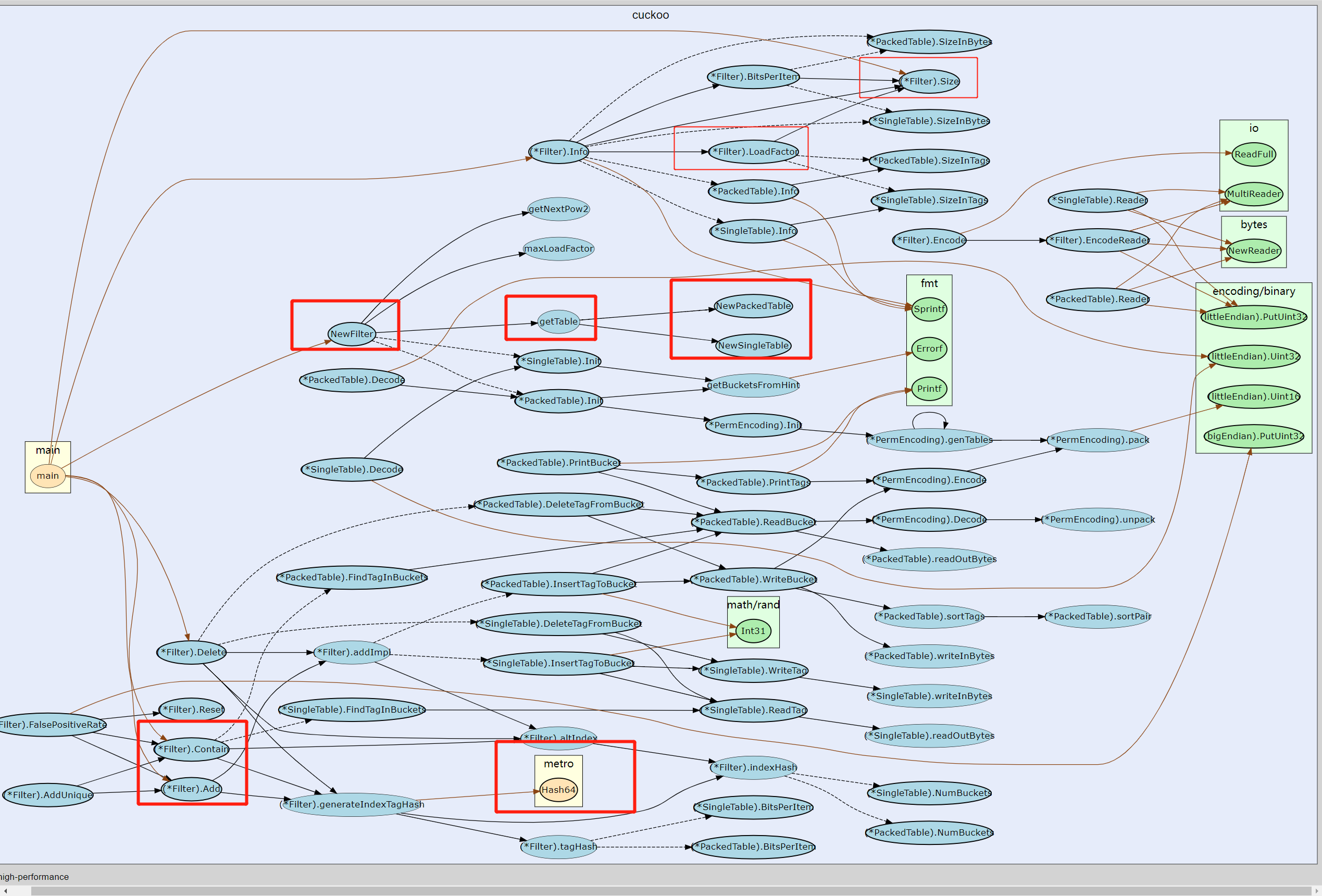
小结
本文概括了 布谷鸟过滤器 的算法描述,并对比了其和 布隆过滤器 的主要差异。在代码实现方面,笔者选择了开源的 linvon/cuckoo-filter ,
着重分析了库的接口设计和主要 API 方法实现。最后顺带提一下,如果读者决定使用 linvon/cuckoo-filter 到项目中,需要注意的是:
库内部并没有做 并发限制,使用 Add, Contain 等方法时可能会遇到常见的 并发竞态 问题,这就要求使用者需要在应用层做好相应的处理。
